Projection azimutale équivalente de Lambert

Projection azimutale équivalente de Lambert
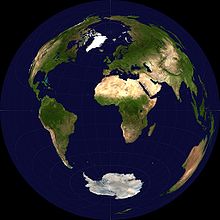
Page d'aide sur l'homonymie Ne doit pas être confondu avec Projection conique conforme de Lambert.
La projection azimutale équivalente de Lambert de la Terre. Son centre est 0° N 0° E dont l'antipode 0° N 180° E se situe près de Kiribati dans l'Océan Pacifique. Cette antipode ainsi projeté forme la circonférence du disque.

La projection azimutale équivalente de Lambert est une manière de projeter une sphère sur un plan, et en particulier, une façon de représenter entièrement la surface de la Terre sous la forme d'un disque. C'est donc une projection cartographique conçue (parmi d'autres) en 1772[1] par le mathématicien alsacien Johann Heinrich Lambert.

Sommaire

Description

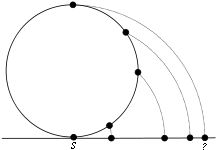
Schématisation en coupe de la projection de la sphère sur le plan.

Cette projection de Lambert "projette directement" sur un plan (projection azimutale) et conserve localement les surfaces (projection équivalente) ; mais ne conserve pas les angles (projection non conforme). Elle est assez proche (à petit échelle) de la projection perspective et plus particulièrement de la projection stéréographique où la représentation des parallèles divergent également.

Définition mathématique

Les formules[2] de cette projection cartographique ont la même forme générale que celles de la projection perspective :

x = α'cos(φ)sin(λ − λ0)

y = α'(sin(φ − φ0) − sin(φ0)cos(φ)(cos(λ − λ0) − 1))

mais α' est plus complexe que α :

\alpha'=\sqrt{{2 \over (1+\cos(\varphi-\varphi_0)+\cos(\varphi_0)\cos(\varphi)(\cos(\lambda-\lambda_0)-1))}}


La transformation inverse est donnée par les formules :

\varphi = \arcsin \left({\sin(\varphi_0) \cos c + { y\cos(\varphi_0) \sin c \over \rho}}\right)

\lambda = \lambda_0 + \arctan\left({x\sin c \over \rho\cos(\varphi_0) \cos c - y\sin(\varphi_0)\sin c}\right)

où

\rho = \sqrt{x^2 + y^2}

c = 2 \arcsin \left({1 \over 2}\rho \right)

Notes et références

  1. ↑ (en) Karen Mulcahy, « Lambert Azimuthal Equal Area », City University of New York. Consulté le 10 novembre 2008
  2. ↑ Source : Lambert Azimuthal Equal-Area Projection.


Voir aussi


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Projection azimutale équivalente de Lambert de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Projection azimuthale équivalente de Lambert — Projection azimutale équivalente de Lambert  Ne doit pas être confondu avec Projection conique conforme de Lambert. La projection azimutale équivalente d …   Wikipédia en Français

  • Projection conique conforme de Lambert — Pour les articles homonymes, voir Lambert.  Ne doit pas être confondu avec Projection azimutale équivalente de Lambert. La pro …   Wikipédia en Français

  • Projection conforme — Projection cartographique Le choix d une projection et la conversion d une projection à une autre comptent parmi les difficultés que les cartographes ont dû affronter. L informatique leur a beaucoup apporté de ce point de vue La projection… …   Wikipédia en Français

  • Lambert-93 — Projection conique conforme de Lambert Pour les articles homonymes, voir Lambert.  Ne doit pas être confondu avec Projection azimutale équivalente de Lambert. La projection conique conforme de Lambert, ou plus simplement, la projection de… …   Wikipédia en Français

  • Lambert 93 — Projection conique conforme de Lambert Pour les articles homonymes, voir Lambert.  Ne doit pas être confondu avec Projection azimutale équivalente de Lambert. La projection conique conforme de Lambert, ou plus simplement, la projection de… …   Wikipédia en Français

  • Projection de Lambert — Projection conique conforme de Lambert Pour les articles homonymes, voir Lambert.  Ne doit pas être confondu avec Projection azimutale équivalente de Lambert. La projection conique conforme de Lambert, ou plus simplement, la projection de… …   Wikipédia en Français

  • Projection de lambert — Projection conique conforme de Lambert Pour les articles homonymes, voir Lambert.  Ne doit pas être confondu avec Projection azimutale équivalente de Lambert. La projection conique conforme de Lambert, ou plus simplement, la projection de… …   Wikipédia en Français

  • Projection cartographique — Le choix d une projection et la conversion d une projection à une autre comptent parmi les difficultés que les cartographes ont dû affronter. L informatique leur a beaucoup apporté de ce point de vue. La projection cartographique est un ensemble… …   Wikipédia en Français

  • Systèmes de projection géographique — Projection cartographique Le choix d une projection et la conversion d une projection à une autre comptent parmi les difficultés que les cartographes ont dû affronter. L informatique leur a beaucoup apporté de ce point de vue La projection… …   Wikipédia en Français

  • Jean Henri Lambert — Johann Heinrich Lambert Pour les articles homonymes, voir Lambert. Johann Heinrich Lambert …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”