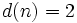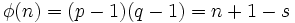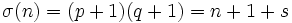- Problème RSA
-
Nombre RSA
Pour les articles homonymes, voir RSA.Les nombres RSA, listés par la compagnie de sécurité RSA Security, sont des grands nombres particuliers (semi-premiers) (c.a.d. des nombres qui ont exactement deux facteurs premiers), liés à l'utilisation de l'algorithme Rivest Shamir Adleman ; ils formaient la base de la Compétition de factorisation RSA, où ces nombres étaient recherchés dans ces factorisations. Des grands prix en argent ont été offerts pour les factorisations réussies de RSA-576 à RSA-2048. La compétition a été stoppée en mai 2007.
Les premiers nombres RSA générés, de RSA-100 à RSA-500, furent étiquetés en référence à leurs nombres de chiffres décimaux ; plus tard, néanmoins, en commençant avec le RSA-576, les chiffres binaires furent comptés à la place. Une exception à ceci est le nombre RSA-617, qui a été créé avant le changement du schéma de numération.
Sommaire
Les mathématiques
Soit n un nombre RSA. Il existe des nombres premiers p et q tels que
.
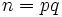Le problème est de trouver ces deux nombres premiers, connaissant seulement n.
Si
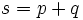; alors les valeurs de certaines fonctions arithmétiques basiques sontLes prix et les records
La table suivante donne une vue d'ensemble de tous les nombres RSA :
Nombre RSA Chiffres décimaux Chiffres binaires Prix offert Factorisé en Factorisé par RSA-100 100 330 Avril 1991 RSA-110 110 364 Avril 1992 RSA-120 120 397 Juin 1993 RSA-129 129 426 100 $ USD Avril 1994 Arjen K. Lenstra et al. RSA-130 130 430 10 avril 1996 Arjen K. Lenstra et al. RSA-140 140 463 2 février 1999 Herman te Riele et al. RSA-150 150 496 retiré mais factorisé en 2004 RSA-155 155 512 22 août 1999 Herman te Riele et al. RSA-160 160 530 1er avril 2003 Jens Franke et al., Université de Bonn RSA-170 170 563 ouvert RSA-576 174 576 10 000 $ USD 3 décembre, 2003 Jens Franke et al., Université de Bonn RSA-180 180 596 ouvert RSA-190 190 629 ouvert RSA-640 193 640 20 000 $ USD 2 novembre 2005 Jens Franke et al., Université de Bonn RSA-200 200 663 9 mai 2005 Jens Franke et al., Université de Bonn RSA-210 210 696 ouvert RSA-704 212 704 30 000 $ USD ouvert RSA-220 220 729 ouvert RSA-230 230 762 ouvert RSA-232 232 768 ouvert RSA-768 232 768 50 000 $ USD ouvert RSA-240 240 795 ouvert RSA-250 250 829 ouvert RSA-260 260 862 ouvert RSA-270 270 895 ouvert RSA-896 270 896 75 000 $ USD ouvert RSA-280 280 928 ouvert RSA-290 290 962 ouvert RSA-300 300 995 ouvert RSA-309 309 1024 ouvert RSA-1024 309 1024 100 000 $ USD ouvert RSA-310 310 1028 ouvert RSA-320 320 1061 ouvert RSA-330 330 1094 ouvert RSA-340 340 1128 ouvert RSA-350 350 1161 ouvert RSA-360 360 1194 ouvert RSA-370 370 1227 ouvert RSA-380 380 1261 ouvert RSA-390 390 1294 ouvert RSA-400 400 1327 ouvert RSA-410 410 1360 ouvert RSA-420 420 1393 ouvert RSA-430 430 1427 ouvert RSA-440 440 1460 ouvert RSA-450 450 1493 ouvert RSA-460 460 1526 ouvert RSA-1536 463 1536 150 000 $ USD ouvert RSA-470 470 1559 ouvert RSA-480 480 1593 ouvert RSA-490 490 1626 ouvert RSA-500 500 1659 ouvert RSA-2048 617 2048 200 000 $ USD ouvert Voir aussi
Liens externes
- (en) RSA Security : Archive sur la compétition de factorisation RSA
- (en) MathWorld : nombre RSA
- Paquet Mathematica pour les nombres RSA
Portail de la cryptologie
Catégorie : Défi RSA
Wikimedia Foundation. 2010.
