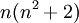- Polynome a valeurs entieres
-
Polynôme à valeurs entières
En mathématiques, un polynôme à valeurs entières P(t) est un polynôme qui prend une valeur entière P(n) pour chaque entier n. D'une manière certaine, chaque polynôme avec des coefficients entiers est à valeurs entières. Voici des exemples simples montrant que le contraire n'est pas vrai : par exemple le polynôme
- t(t + 1)/2
donnant les nombres triangulaires renvoie des valeurs entières lorsque t = n est un entier. C'est parce que n ou n + 1 doivent être un nombre pair.
En fait, les polynômes à valeurs entières peuvent être décrits complètement. À l'intérieur de l'anneau des polynômes Q[t] des polynômes à coefficients rationnels, le sous-anneau des polynômes à valeurs entières est un groupe abélien libre. Il possède comme base les polynômes
- Pk(t) = t(t − 1)...(t − k + 1)/k!
pour k = 0,1,2, ...
Diviseurs premiers fixés
Ce concept peut être utilisé efficacement pour résoudre les questions ayant trait aux diviseurs fixés de polynômes. Par exemple, les polynômes P à coefficients entiers qui prennent toujours des valeurs en nombre pair sont juste ceux tels que P/2 est à valeurs entières. Ceux-ci sont à leur tour ceux exprimés comme sommes de polynômes de base, avec des coefficients pairs.
Dans les questions de théorie des nombres sur les nombres premiers, tel que l'hypothèse H de Schinzel et la conjecture de Bateman-Horn, c'est une question d'importance fondamentale de comprendre la question lorsque P ne possède pas de diviseur premier fixé (ceci a été appelé la propriété de Bunyakovsky, en l'honneur de Viktor Bunyakovsky). En écrivant P en termes de polynômes de base, nous voyons que le diviseur premier fixé le plus élevé est aussi le PGCD des cofficients dans une telle représentation. Donc, la propriété de Bunyakovsky est l'équivalent de coefficients premiers entre eux.
Comme exemple, la paire de polynômes n et n2 + 2 violent cette condition pour p = 3 : pour chaque n le produit
est divisible par 3. En conséquence, il ne peut pas exister infiniment de paires premières de n et n2 + 2. La divisibilité est attribuable à la représentation alternative
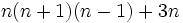 .
.
Catégorie : Arithmétique
Wikimedia Foundation. 2010.