Planche de Galton
- Planche de Galton
-
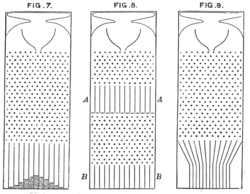
La planche dessinée par Francis Galton en 1889
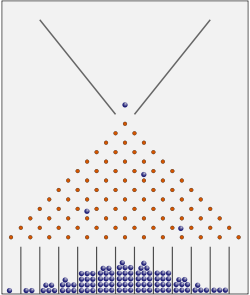
Une vue schématique du dispositif
Une planche de Galton est un dispositif inventé par Francis Galton qui illustre la convergence d'une loi binomiale vers une loi normale.
Des clous sont plantés sur la partie supérieure de la planche, de telle sorte qu'une bille lâchée sur la planche passe soit à droite soit à gauche pour chaque rangée de clous. Dans la partie inferieure les billes sont rassemblées en fonction du nombre de passages à gauche et de passage à droite qu'elles ont fait.
Ainsi chaque case correspond à un résultat possible d'une expérience binomiale (en tant qu'une expérience de Bernoulli répétée) et on peut remarquer que la répartition des billes dans les cases approche la forme d'une courbe de Gauss, autrement dit : la loi binomiale converge vers la loi normale. Il s'agit donc d'une illustration au théorème de Moivre-Laplace.
Voir aussi
Lien externe
 Portail des probabilités et des statistiques
Portail des probabilités et des statistiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Planche de Galton de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Francis Galton — vers 1850. Biographie Naissance 16 fé … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Theoreme de Moivre-Laplace — Théorème de Moivre Laplace Une planche de Galton illustre le fait que la loi binomiale tend vers la loi normale Le Théorème de Moivre Laplace stipule que si la variable Sn suit une loi binomiale d ordre n et de paramètre … Wikipédia en Français
Théorème de Moivre-Laplace — Une planche de Galton illustre le fait que la loi binomiale tend vers la loi normale. En probabilités, le Théorème de Moivre Laplace stipule que si la variable Xn suit une loi binomiale d ordre n et de paramètre … Wikipédia en Français
Théorème de moivre-laplace — Une planche de Galton illustre le fait que la loi binomiale tend vers la loi normale Le Théorème de Moivre Laplace stipule que si la variable Sn suit une loi binomiale d ordre n et de paramètre … Wikipédia en Français
Distribution gaussienne — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Distribution normale — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Loi Normale — Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français
Loi Normale Reduite — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition … Wikipédia en Français



