- Philippe Oechslin
-
Table arc-en-ciel
En cryptologie, une table arc-en-ciel (aussi appelée Rainbow Table) est une structure de données créée en 2003 par Philippe Oechslin pour retrouver un mot de passe à partir de son empreinte. Il s'agit d'une amélioration des compromis temps-mémoire proposés par Martin Hellman dans les années 1980.
Sommaire
Aperçu
Plusieurs tables peuvent être produites pour améliorer les chances de réussite. Les tables contiennent une grande quantité de chaînes qui proposent en alternance un mot de passe suivi de son empreinte. Une « fonction de réduction » qui varie selon la position dans la table permet de recréer un autre mot de passe à partir de l'empreinte et ainsi de suite. L'algorithme développé par Oechslin optimise la détection des collisions et le parcours dans la table. Des solutions pour réduire la taille de la table ont également été proposées.
L'algorithme, déjà efficace avec des mots de passe correctement chiffrés (le mot de passe Windows "Fgpyyih804423" est déchiffré en 160 secondes[1]) l'est à fortiori avec les mots de passe de LAN Manager. Les mots de passe de LM sont ainsi trouvés en l'espace de quelques secondes s'ils sont alphanumériques. Les tables peuvent être utilisées pour d'autres fonctions de hachage comme MD5 ou encore SHA-1, ces dernières sont toutefois nettement plus robustes du point de vue cryptographique que LAN Manager et nécessitent des tables plus grandes. La sécurité calculatoire du système de Microsoft a toujours été faible mais il a été remplacé par les NT-hash dans Windows NT et les versions ultérieures de Windows.
Une bonne protection - pour le moment (2008) - consiste à introduire dans le mot de passe un caractère non alphanumérique ou, ce qui est facile pour les francophones, un caractère national.
Description détaillée
Création de la table
La table arc-en-ciel est constituée de paires de mots de passe (ie. chaque ligne possède un mot de passe de départ et un mot de passe d'arrivée). Pour calculer la table, on établit des chaînes grâce à un mot de passe initial. Celui-ci subit une série de réductions et de hachage afin d'obtenir des éléments intermédiaires (mots de passe et empreintes correspondantes). La fonction de réduction transforme une empreinte en un nouveau mot de passe. Afin d'éviter des problèmes de collision, plusieurs fonctions de réduction sont utilisées. Après plusieurs milliers d'itérations, on obtient un mot de passe en bout de chaîne. C'est celui-ci qui est stocké avec le mot de passe à l'origine de cette chaîne. Le reste de la chaîne n'est pas conservée afin de limiter la mémoire nécessaire. Il est toutefois possible de les retrouver en calculant l'ensemble de la chaîne à partir de l'élément en tête de liste.
On recommence avec un autre mot de passe pour établir une nouvelle chaîne et ainsi de suite jusqu'à constituer une table dont les statistiques sont suffisantes pour garantir le succès de l'attaque.
Plus formellement, le calcul d'une chaîne se fait comme suit à partir d'un mot de passe initial P et de fonctions de réduction (différentes à chaque itération pour limiter les collisions) :
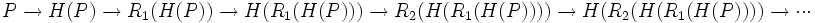
Recherche du mot de passe
On considère une empreinte H engendrée à partir d'un mot de passe P. La première étape consiste à prendre H, lui appliquer la dernière fonction de réduction utilisée dans la table, et regarder si ce mot de passe apparaît dans la dernière colonne de la table. Si cette occurrence n'est pas trouvée alors on peut déduire que l'empreinte ne se trouvait pas à la fin de la chaîne considérée. Il faut revenir un cran en arrière. On reprend H, on lui applique l'avant-dernière fonction de réduction, on obtient un nouveau mot de passe. On hache ce mot de passe, on applique la dernière fonction de réduction et on regarde si le mot de passe apparaît dans la table.
Cette procédure itérative se continue jusqu'à ce que le mot de passe calculé en fin de chaîne apparaisse dans la table (si rien n'est trouvé, l'attaque échoue). Une fois le mot de passe découvert dans la dernière colonne, on récupère le mot de passe qui se trouve dans la première colonne de la même ligne. On calcule à nouveau la chaîne tout en comparant à chaque itération l'empreinte obtenue à partir du mot de passe courant avec l'empreinte H du mot de passe inconnu P. S'il y a égalité, alors le mot de passe courant correspond à celui recherché et l'attaque a réussi ; plus précisément, on a trouvé un mot de passe dont l'empreinte est la même que celle de P, ce qui est suffisant.
Exemple
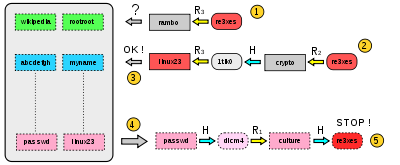
- À partir d'une empreinte ("re3xes"), on calcule la dernière réduction utilisée dans la table et on regarde si le mot de passe apparaît dans la dernière colonne de la table (étape 1)
- Si le test échoue ("rambo" n'apparaît pas dans la table), on passe au point 2 où l'on calcule une chaîne avec les deux dernières réductions.
- Si ce test échoue à nouveau, on recommence avec 3 réductions, 4 réductions, etc. jusqu'à trouver une occurrence du mot de passe dans la table. Si aucune chaîne ne correspond alors l'attaque échoue.
- Si le test réussit (étape 3, ici "linux23" apparaît en fin de chaîne et également dans la table), on récupère le mot de passe à l'origine de la chaîne qui a abouti à "linux23". Il s'agit ici de "passwd".
- On génère la chaîne (étape 4) et on compare à chaque itération l'empreinte avec l'empreinte recherchée. Le test est concluant, on trouve ici l'empreinte "re3xes" dans la chaîne. Le mot de passe courant ("culture") est celui qui a engendré la chaîne : l'attaque a réussi.
Contre-mesures
L'efficacité des tables diminue de façon significative lorsque les fonctions de hachage sont combinées à un sel. Dans le cadre d'un système de mots de passe, le sel est une composante aléatoire ou un compteur qui change en fonction de l'utilisateur. Si deux utilisateurs ont le même mot de passe, le sel permet d'éviter que les empreintes soient identiques. De manière informelle, le sel consiste en une opération du type :
empreinte = h(mot_de_passe + sel)
où l'opération + peut être une concaténation ou une opération plus complexe
Cette mesure augmente la complexité de l'attaque : il faut non seulement inverser la fonction grâce aux tables mais il faut encore explorer l'ensemble des possibilités induites par la présence du sel. Si l'attaque réussit, il faut encore retirer le sel du mot de passe.
En pratique, certaines applications n'utilisent pas de sel et sont vulnérables. En outre, le sel doit avoir une longueur suffisante pour augmenter sensiblement la complexité. Un sel trop court (par exemple 4 bits) ne multiplierait la complexité que d'un facteur de 16. Dans le système GNU/Linux, la fonction de hachage utilisée est du MD5 avec un sel de 8 caractères en ASCII ce qui rend l'attaque impossible en pratique.
Notes & références
Voir aussi
Articles connexes
Liens externes
- (fr) Utilisation de Rainbow-Tables, démonstrations et téléchargements.
- (fr) Les compromis temps-mémoire et leur utilisation pour casser les mots de passe Windows, par P. Oechslin
- (en) Philippe Oechslin (LASEC/EPFL)
- (en) Attacking NTLM with Precomputed Hashtables
- (en) Site du projet TMRL DRTG. Projet de calcul réparti utilisant BOINC afin de créer des tables arc-en-ciel.
- (en) Site du projet Free Rainbow Tables. Autre projet de calcul réparti.
- (en) Rainbow Tables Download
- Portail de la sécurité informatique
- Portail de la cryptologie
Catégorie : Cryptanalyse
Wikimedia Foundation. 2010.