SHA-1

Une itération de SHA-1 avec deux rotations vers la gauche et une fonction non-linéaire qui dépend du numéro d'itération, deux autres variables interviennent à chaque tour

SHA-1 (Secure Hash Algorithm) est une fonction de hachage cryptographique conçue par la National Security Agency des États-Unis (NSA), et publiée par le gouvernement des États-Unis comme un standard fédéral de traitement de l'information (Federal Information Processing Standard du National Institute of Standards and Technology (NIST)). Elle produit un résultat (appelé « hash » ou condensat) de 160 bits.

Pour les détails de l'algorithme et son implémentation, voir l'article Spécifications SHA-1.

Origine : SHA-0 et SHA-1

Le SHA-1 est le successeur du SHA-0 qui a été rapidement mis de côté par le NIST pour des raisons de sécurité insuffisante. Le SHA-0 était légitimement soupçonné de contenir des failles qui permettraient d'aboutir rapidement à des collisions (deux documents différents qui génèrent le même condensat). Face à la controverse soulevée par le fonctionnement du SHA-0 et certains constats que l'on attribue au NSA, le SHA-0 s'est vu modifié peu après sa sortie (1993) et complexifié pour devenir le SHA-1 (1995). Une collision complète sur le SHA-0 a été découverte par Antoine Joux et al. en août 2004 et laisse penser que le SHA-1 pourrait lui aussi subir une attaque.

Attaques

Une attaque basée sur le paradoxe des anniversaires permet de trouver une collision complète sur le SHA-1 avec un nombre d'opérations de l'ordre de 2⁸⁰.

En 2005, Rijmen et Oswald ont publié une attaque sur une version simplifiée du SHA-1 (53 tours), leur attaque permet de trouver une collision avec moins de 2⁸⁰ opérations.

En février 2005, Bruce Schneier a fait état d'une attaque sur la version complète du SHA-1 par l'équipe chinoise de Wang, Yin et Yu. Leur méthode permet de trouver :

• une collision dans le SHA-1 complet de 128 bits avec 2⁶⁹ opérations au lieu de 2⁸⁰ par le paradoxe des anniversaires
• une collision dans le SHA-0 complet avec seulement 2³⁹ opérations
• une collision dans une version simplifiée du SHA-1 (58 tours) avec 2³³ opérations

La description de l'attaque a été publiée en juin 2005.

Le 17 août 2005, une amélioration de l'attaque a été annoncée par Wang et al. à la conférence CRYPTO 2005, la complexité passe ainsi de 2⁶⁹ à 2⁶³, soit une division par 64 de la complexité originale.

Lors de l'Eurocrypt 2009 (avril), une amélioration^[1] de l'attaque aurait permis de réduire à nouveau sa complexité jusqu'à atteindre 2⁵², soit quelques semaines de calculs sur un PC standard. Toutefois, ces résultats furent démentis et l'article^[2] fut retiré^[3] suite à la découverte d'une erreur dans l'évaluation de cette complexité.

Conséquences

Même si un gain de 2¹⁷ opérations permet de diviser le temps de recherche par un facteur de 131 072, l'attaque avec ses 2⁶³ opérations est à la limite de ce qui est réalisable. Adi Shamir a toutefois laissé entendre que l'attaque pouvait probablement être abordée via un calcul distribué à l'échelle planétaire.

La règle veut qu'une attaque plus rapide que la recherche exhaustive rende l'algorithme non sûr du point de vue cryptographique. De plus, avec 2⁶³ opérations, l'attaque est en dessous des 2⁶⁴ nécessaires pour une recherche exhaustive sur un MD5 (qui n'est plus conseillé pour les nouvelles applications). Ayant perdu une longueur d'avance dès l'annonce de l'attaque de Wang et al., SHA-1 a été retiré progressivement des applications cryptographiques au profit de SHA-256 ou des autres fonctions de hachage comme Whirlpool ou Tiger. En conséquence, une compétition a été organisée par la NIST, afin de trouver un nouveau standard de hachage (SHA-3) comme cela fut le cas il y a quelques années pour la cryptographie symétrique avec AES.

L'attaque produite par Wang et al. ne concerne que des collisions quelconques (tout comme leur fameuse collision complète sur le MD5). C’est-à-dire que l'on peut trouver deux messages au contenu aléatoire qui produisent la même signature. En revanche, à partir d'une signature donnée, il est impossible de forger un second message qui conduise à la même valeur. Or, c'est ce type d'attaque qui pourrait mettre en péril les applications comme PGP et l'authenticité des données.

Fonctionnement du SHA-1

Le SHA-1 prend un message d'un maximum de 2⁶⁴ bits en entrée. Son fonctionnement est similaire à celui du MD4 ou MD5 de Ronald Rivest. Quatre fonctions booléennes sont définies, elles prennent 3 mots de 32 bits en entrée et calculent un mot de 32 bits. Une fonction spécifique de rotation est également disponible, elle permet de déplacer les bits vers la gauche (le mouvement est circulaire et les bits reviennent à droite). Une de ces rotations n'était pas présente dans le SHA-0, elle permet de casser certaines caractéristiques linéaires dans la structure. Cela permet d'éviter une attaque sur les bits neutres décrite par Eli Biham, technique reprise pour calculer la collision complète sur SHA-0 (Antoine Joux et al.).

Le SHA-1 commence par ajouter à la fin du message un bit à 1 suivi d'une série de bits à 0, puis la longueur du message initial (en bits) codée sur 64 bits. La série de 0 a une longueur telle que la séquence ainsi prolongée a une longueur multiple de 512 bits. L'algorithme travaille ensuite successivement sur des blocs de 512 bits.

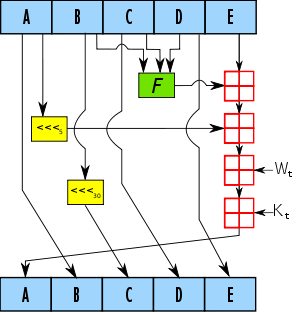
Pour chaque bloc l'algorithme calcule 80 tours (ou rondes, « rounds » en anglais) successifs et applique une série de transformations sur l'entrée. La première étape consiste à calculer 80 valeurs sur 32 bits. Les 16 premières valeurs sont obtenues directement à partir du bloc « message » en entrée. Les 64 autres sont calculées successivement. Le SHA-1 les obtient grâce à une rotation (absente dans SHA-0) qui est appliquée sur le résultat d'un XOR, il utilise pour cela 4 mots obtenus dans les itérations précédentes. On définit ensuite 5 variables qui sont initialisées avec des constantes (spécifiées par le standard), le SHA-1 utilise encore 4 autres constantes dans ses calculs. Si un bloc de 512 bits a déjà été calculé auparavant, les variables sont initialisées avec les valeurs obtenues à la fin du calcul sur le bloc précédent.

Il s'ensuit 80 tours qui alternent des rotations, des additions entre les variables et les constantes. Selon le numéro du tour, le SHA-1 utilise une des quatre fonctions booléennes. L'une de ces fonctions est appliquée sur 3 des 5 variables disponibles. Les variables sont mises à jour pour le tour suivant grâce à des permutations et une rotation. En résumé, le SHA-1 change sa méthode de calcul tous les 20 tours et utilise les sorties des tours précédents.

À la fin des 80 tours, on additionne le résultat avec le vecteur initial. Lorsque tous les blocs ont été traités, les cinq variables concaténées (5 × 32 = 160 bits) représentent la signature.

Pour plus de détails, voir Spécifications SHA-1.

Exemples

Voici la signature obtenue sur une phrase :

SHA1("Wikipédia, l'encyclopédie libre et gratuite") = AFBA34A2A11AB13EEBA5D0A7AA22BBB6120E177B

En modifiant un caractère, la signature change radicalement :

SHA1("Wikipédia, l'encyclopédie libre et gratuitE") = 9BEF2485410E9378BC9ADFB3E32236AF4F683FA2

Le SHA-1 est un excellent générateur de nombres pseudo-aléatoires (comme beaucoup de fonctions de hachage) et il passe avec succès tous les tests statistiques. Un test conduit par Eric Filiol a confirmé la qualité mathématique des sorties qui sont « plus aléatoires » que celles de RIPEMD-160 ou SHA-0.

Le SHA-1 en mode chiffrement

Contrairement à ce que l'on peut penser, une fonction de hachage peut être utilisée pour chiffrer moyennant quelques modifications. Dans le cas du SHA-1, il existe un algorithme de chiffrement symétrique, SHACAL que l'on doit à Helena Handschuh et David Naccache.

La famille SHA

Une itération de SHA-2

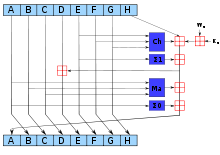
Des versions offrant plus de sécurité sont également disponibles : SHA-256, SHA-384 et SHA-512. Comme leur nom l'indique, ces versions fournissent des signatures de 256, 384 et 512 bits. Une variante a été récemment ajoutée, le SHA-224 assure une compatibilité avec la longueur de deux clés qui seraient utilisées pour du Triple DES (4 clés de 56 bits, le 3DES utilise 3 clés de 56 bits).

Notes et références

E.A.Grechnikov,Collisions for 72-step and 73-step SHA-1: Improvements in the Method of Characteristics, (http://eprint.iacr.org/2010/413)

Liens externes

• (fr) Un calculateur de hash en SHA-1
• (en) SHA1 dictionary attack
• (en) Vidéo de CRYPTO 2005, avec la présentation de l'attaque améliorée par Adi Shamir
• (en) Slides d'Adi Shamir à CRYPTO 2005[PDF]
• (en) A New Statistical Testing for Symmetric Ciphers and Hash Functions, test statistique de Eric Filiol
• (en) SHACAL[PDF], description de SHA-1 en mode chiffrement (SHACAL)

• Portail de la cryptologie