Petit théorème de Picard
- Petit théorème de Picard
-
Théorèmes de Picard
Les théorèmes de Picard, du mathématicien Émile Picard, sont au nombre de deux :
Le petit théorème de Picard dit qu'une fonction entière non constante prend tout nombre complexe comme valeur, sauf peut-être un.
Le grand théorème de Picard dit qu'une fonction ayant une singularité essentielle prend, sur tout voisinage de cette singularité, tout nombre complexe une infinité de fois comme valeur, sauf peut-être un.
Remarques
- Le « sauf peut-être un » dans ces énoncés est nécessaire, comme le montrent les exemples suivants. La fonction entière
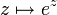 ne s'annule pas. Elle possède même une singularité essentielle en l'infini (c'est fonction transcendante). La fonction
ne s'annule pas. Elle possède même une singularité essentielle en l'infini (c'est fonction transcendante). La fonction 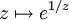 est un exemple de fonction ne s'annulant pas avec singularité essentielle bornée (se trouvant en 0).
est un exemple de fonction ne s'annulant pas avec singularité essentielle bornée (se trouvant en 0).
- Le petit théorème se déduit immédiatement du grand, car toute fonction entière est soit polynôme soit elle possède une singularité essentielle à l'infini.
- Une récente conjecture de Bernhard Elsner[1] est liée au grand théorème de Picard : Soit D − {0} le disque unité épointé et U1,U2,...,Un un recouvrement de D − {0} par des ouverts. Sur chaque ouvert Uj soit fj une fonction holomorphe injective telle que dfj = dfk sur toutes les intersections
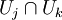 . Alors ces différentielles se recollent en une 1-forme méromorphe sur le disque D. (Si le résidu est nul, la conjecture découle du grand théorème de Picard.)
. Alors ces différentielles se recollent en une 1-forme méromorphe sur le disque D. (Si le résidu est nul, la conjecture découle du grand théorème de Picard.)
Voir aussi
Références
- ↑ Ann. Institut Fourier 49-1 (1999) p.330
 Portail des mathématiques
Portail des mathématiques
Catégories : Analyse complexe | Théorème de mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Petit théorème de Picard de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Théorème de Picard-Lindelöf — Théorème de Cauchy Lipschitz Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. Le … Wikipédia en Français
Theoreme de Liouville (variable complexe) — Théorème de Liouville (variable complexe) Pour les articles homonymes, voir Théorème de Liouville. Joseph Liouville. En analyse complexe, le thé … Wikipédia en Français
Théorème de liouville (variable complexe) — Pour les articles homonymes, voir Théorème de Liouville. Joseph Liouville. En analyse complexe, le thé … Wikipédia en Français
Théorème de Liouville (variable complexe) — Pour les articles homonymes, voir Théorème de Liouville. Joseph Liouville. En analyse complexe, le théorème de Liouville est un résultat portant sur les fonctions entière … Wikipédia en Français
Theoreme de Cauchy-Lipschitz — Théorème de Cauchy Lipschitz Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. Le … Wikipédia en Français
Théorème de cauchy-lipschitz — Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. Le … Wikipédia en Français
Theoremes de Picard — Théorèmes de Picard Les théorèmes de Picard, du mathématicien Émile Picard, sont au nombre de deux : Le petit théorème de Picard dit qu une fonction entière non constante prend tout nombre complexe comme valeur, sauf peut être un. Le grand… … Wikipédia en Français
Théorèmes de picard — Les théorèmes de Picard, du mathématicien Émile Picard, sont au nombre de deux : Le petit théorème de Picard dit qu une fonction entière non constante prend tout nombre complexe comme valeur, sauf peut être un. Le grand théorème de Picard… … Wikipédia en Français
Théorèmes de Picard — En analyse complexe, les théorèmes de Picard, du mathématicien Émile Picard, sont au nombre de deux : Le petit théorème de Picard dit qu une fonction entière non constante prend tout nombre complexe comme valeur, sauf peut être un. Le grand… … Wikipédia en Français
Émile Picard — Pour les articles homonymes, voir Picard (homonymie). Émile Picard Émile Picard devant l Académie française, photo Meurisse, 1926 … Wikipédia en Français
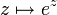 ne s'annule pas. Elle possède même une singularité essentielle en l'infini (c'est fonction transcendante). La fonction
ne s'annule pas. Elle possède même une singularité essentielle en l'infini (c'est fonction transcendante). La fonction 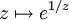 est un exemple de fonction ne s'annulant pas avec singularité essentielle bornée (se trouvant en 0).
est un exemple de fonction ne s'annulant pas avec singularité essentielle bornée (se trouvant en 0).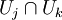 . Alors ces différentielles se recollent en une 1-forme méromorphe sur le disque D. (Si le résidu est nul, la conjecture découle du grand théorème de Picard.)
. Alors ces différentielles se recollent en une 1-forme méromorphe sur le disque D. (Si le résidu est nul, la conjecture découle du grand théorème de Picard.)