Perspective visuelle

Pour les articles homonymes, voir Perspective.

La perspective visuelle ou oculaire est l’ensemble des transformations par lesquelles une portion du monde spatial tridimensionnel (et euclidien à l’échelle de l’homme) est perçue par la surface bidimensionnelle et courbe (donc non-euclidienne) de l’œil, indépendamment des propriétés stéréoscopiques de la vision binoculaire frontale. Du point de vue mathématique, elle est une projection par laquelle la dimension métrique des objets se trouve convertie en dimension angulaire. La géométrie projective est la branche des mathématiques qui modélise les propriétés de cette projection, indépendamment de la réalité physiologique l'œil.

Notions générales

L’œil considéré individuellement (vision monoculaire) fonctionne comme une lentille stigmatique qui fait correspondre à chaque point de l’espace du cône de vision un point sur la surface rétinienne.

Un même objet apparaît de façon différente à l’œil en fonction de 3 paramètres :

• sa distance à l’œil
• son excentration par rapport à l’axe du regard
• son inclinaison dans les 3 directions

Un segment placé devant soi apparaît d’autant plus grand qu’il est proche, et qu’il se situe dans un plan perpendiculaire à l’axe du regard. Il apparaît d’autant plus courbe qu’il est proche, et qu’il est excentré par rapport à l’axe du regard.

Le processus cognitif par lequel le cerveau reconstruit mentalement dans l’espace les formes des objets perçus sur la surface de la rétine participe si étroitement à l’expérience visuelle qu’il demeure largement pré-conscient. On perçoit comme parallèles deux rails de train, alors qu’on constate bien sur une photographie que leurs lignes se rejoignent à l’horizon, et qu’elles sont toujours incurvées en cloche (vers l’intérieur).

Précisions (et réserves) sur quelques notions sous-jacentes

La perception en perspective est une propriété fondamentale de la vision et une conséquence directe de l’anatomie de l’œil. À ce titre, elle n’est pas la même pour chaque espèce animale. On trouve très souvent dans la littérature les expressions champ visuel et cône de vision ; les schémas explicatifs et les illustrations y présentent souvent la perspective comme une projection sur une surface plane qui correspond à la section orthogonale du cône de vision ; enfin les mêmes illustrations et schémas se limitent à la représentation d’un seul œil.

• Comme le suggère la sémantique, on parle de champ visuel pour décrire à la fois la portion d’espace visible et l’expression de la vision, qui est une surface.
• En toute rigueur mathématique, un cône est « une surface réglée définie par une droite (d), appelée génératrice, passant par un point fixe S appelé sommet et un point variable décrivant une courbe plane fermée (c), appelée courbe directrice ». Parler de « cône de vision », c’est a) considérer la vision comme monoculaire (le sommet est le point de convergence dans l’œil) et 2) sous-tendre que l’ouverture du champ visuel est strictement inférieure à 180° dans toutes les directions.
• Parler de l’œil au singulier, et le comparer à la lentille unique d’une caméra, suggère une fois de plus une vision strictement monoculaire.

Or tous les vertébrés possèdent deux yeux. Chez les mammifères, les deux champs visuels se recoupent, de sorte que la vision binoculaire est, pour la plupart d’entre eux, plus que la somme de deux visions monoculaires.

L’ouverture du champ visuel est très variable d’une espèce animale à l’autre. Ainsi, certains mammifères comme le chat ou le cheval ont un champ visuel qui dépasse très largement 180° pour chaque œil, ce qui exclut de projeter ce champ visuel sur une surface plane. Même ceux qui ont le champ plus commun de 170° pour chaque œil atteignent, du fait de la latéralisation oculaire, un champ combiné supérieur à 200°, ce qui rend tout aussi impossible une projection plane. La vision binoculaire frontale monodirectionnelle est en fait caractéristique d’une minorité de vertébrés, dont l’homme. Pour ce dernier, cela implique qu’il n’y a pas un, mais deux sommets pour le « cône de vision », et aussi deux axes du regard à peu près parallèles… En contrepartie, le champ visuel total est pour l’homme de l’ordre de 180° latéralement et 125° verticalement, ce qui permet opportunément de délimiter « ce qui est visible pour lui » à « ce qu’il a devant lui ». C’est à cette seule condition qu’il peut y avoir une projection de l’espace visible sur la surface plane et finie d’une ellipse visuelle – ce qu’on entend en fait communément par « champ visuel ».

Cette ellipse est parfois simplifiée sous la forme de cercle (ce qui correspond à la section orthogonale d’un cône de révolution, alors que le cône visuel des animaux est « aplati »), tandis qu’on la retrouve approximée par un rectangle très oblong dans les proportions dites panoramiques des écrans de cinéma (voir 16/9). Une autre différence entre l’œil et la lentille d’une caméra est que champ visuel n’est pas homogène en termes de performance (acuité, photosensibilité, polychromie) et d’attention : la scrutation active est réservée au centre, et la performance décroît par palier vers la périphérie du regard. L’intérêt de cet enchâssement des cônes de vision, c’est que seul le champ de vision attentive est pertinent lorsqu’on « observe » une image.

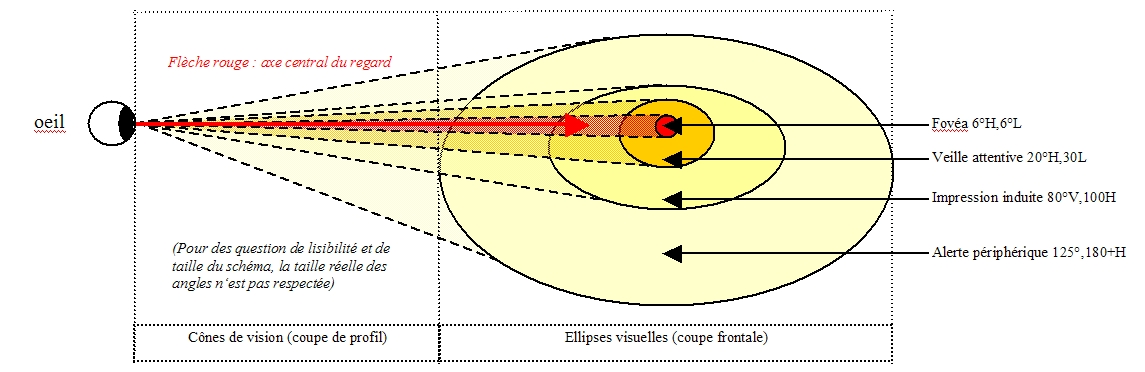illustration 1 : cônes et ellipses de vision par zones de performance visuelle

Lois de la perspective

illustration 2 : apparence visuelle d’un segment AB dans l’espace. L’illustration permet de vérifier que la perspective est une application qui fait correspondre à des mesures métriques dans l’espace des mesures angulaires sur une surface. Cette projection est surjective, puisque plusieurs objets distincts de l’espace (ici AiBi, AjBi, AjBj) peuvent avoir la même projection (c’est à dire une apparence) en perspective, et inversement, une seule forme apparente correspond à un nombre infini d’objets possibles dans l’espace.

Illustration 3 : apparence courbe des segments de l’espace. C’est en o et seulement en o que le plan est orthogonal à l’axe du regard. Par simple application du théorème de Pythagore, OA= (oO2+oA2)1/2 et Oi = (oO2+oi2)1/2 Donc oO < (iO = jO) < (AO = BO =CO = DO) Un segment apparaissant d’autant plus petit qu’il est éloigné, on en déduit que AD apparaît plus petite que ij, et que, de façon générale, pour tout couplet (x, y ; x є AB ; y є CD ; xy ║AD), xy décroît tandis que xi croît. On en déduit que les cotés du carré, et de façon générale toute droite du plan ne passant pas par o, apparaissent en perspective sous forme de courbes en cloche placées entre leur « original réel» et O et qui tendent en leur 2 extrémités vers la droite parallèle à leur « original » passant par o.

Lois de la perspective

Les illustration 2 et 3 permettent de se convaincre des principes suivants :

• A inclinaison constante, la dimension apparente d’un segment est fonction inverse de sa distance à l’œil

• A distance constante, la dimension apparente d’un segment décroît tandis qu’augmente l’angle d’inclinaison du segment par rapport au plan perpendiculaire au regard

• Tout segment de l’espace qui ne passe pas par le centre du regard apparaît courbé en perspective ; l’intensité de la courbure croît avec l’excentration.

De ces principes fondamentaux se déduisent des principes plus complexes pour les solides visibles. Par exemple :

• Deux droites parallèles dans l’espace réel apparaissent en perspective comme des courbes en cloche convergeant vers le même point (qui peut être à l’intérieur comme à l’extérieur de l’ellipse visuelle).

• Une surface carrée perpendiculaire à l’axe du regard dans le monde réel apparaît en perspective comme un quasi-trapèze dont aucun des angles n’est droit, et dont les cotés sont incurvés en cloche vers l’extérieur du regard.

• Plus une surface carrée est proche (i.e. envahit le champ visuel), plus son apparence est déformée en termes d’angles et de courbures. Plus elle s’éloigne (i.e. rétrécit), plus elle prend l’apparence simple d’une projection euclidienne d’une espace sur un plan.

• un cube dont aucune des faces n’est parallèle à l’axe du regard présente forcément 3 faces, dont aucun angle n’est droit, et dont les 9 arêtes visibles sont des courbes qui convergent 3 par 3 vers 3 points.

Imitation graphique des effets de la perspective visuelle

(voir aussi perspective graphique)

L’expression mathématique exacte de ces principes est évidemment très complexe. Elle l’est d’autant plus qu’on considère les propriétés de solides et non l’espace point par point. Même des notions en apparence simple comme la « distance d’un objet à l’œil » ou d’ « angle solide » d’une surface dans l’espace se révèlent particulièrement ardues voire inapplicables dès qu’on essaie de les employer avec rigueur. Ceci explique que la plupart des représentations graphiques qui cherchent à en rendre compte de la perspective visuelle soient des approximations plus ou moins réalistes (voir photoréalisme), voire des conventions qui renoncent à un aspect ou à un autre de la réalité.

Dans l’imagerie de synthèse, ces difficultés n’existent pas du fait du mode de calcul point par point, lui-même rendu possible de la puissance opératoire des ordinateurs modernes. La perspective est simulée par le logiciel de façon photo-réaliste à chaque instant, de sorte qu’elle apparaît comme « allant de soi ». En fait, la perspective est la seule composante du processus de création d’une image qui ne soit pas construite par le graphiste, mais posée par le logiciel. En le faisant « tourner » ou en tournant autour de lui en temps réel selon des lois de transformation qui lui échappent, le graphiste a l’illusion de générer un solide tridimensionnel, une « figure 3D » - alors qu’il a un écran bidimensionnel devant les yeux.

voir aussi

• optique
• géométrie descriptive