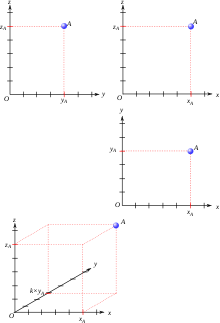
Perspective cavalière

Perspective cavalière
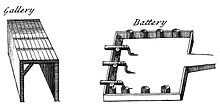Parties de fortification : gallery (à gauche) en perspective avec point de fuite et battery (à droite) en perspective cavalière (Cyclopaedia vol. 1, 1728)
Report des coordonnées pour placer un point sur une perspective cavalière


La perspective cavalière est une manière de représenter en deux dimensions des objets en volume. Cette représentation ne présente pas de point de fuite : la taille des objets ne diminue pas lorsqu'ils s'éloignent. C'est une forme particulière de perspective axonométrique, où l'on situe les points grâce à leurs coordonnées dans un repère formé de trois axes.

Dans cette perspective, deux des axes sont orthogonaux et ont un facteur de report de 1. Le troisième axe est incliné, en général de 30 ou 45° par rapport à l'horizontale, appelé « angle de fuite », et a un facteur de report inférieur à 1, en général 0,7 ou 0,5[1], [2]

Cette perspective ne prétend pas donner l'illusion de ce qui peut être vu, mais simplement donner une information sur la notion de profondeur.

Simple à réaliser, c'est une perspective naïve qui peut traduire un manque de « vision dans l'espace ». Trop souvent utilisée dans les dessins à main levée, elle est malgré tout à déconseiller par son ambiguïté de représentation : un objet éloigné d'un autre peut sembler être plutôt au-dessus ou au-dessous.

Cette représentation était utilisée initialement pour la conception des fortifications militaires. Le « cavalier » est un promontoire de terre situé en arrière des fortifications et qui permet de voir par-dessus, et donc de voir les assaillants[3]. La perspective cavalière était donc la vue que l'on avait du haut du cavalier (les anglais utilisent parfois le terme de « high view point », en français « point de vue de haut »). Certains avancent également que c'est la vue qu'un cavalier a du haut de son cheval[4].

Approche mathématique

Si le plan face au lecteur est le plan xz et que l'axe de fuite est l'axe y, avec un angle de fuite α et un rapport k, alors un point dans l'espace de coordonnées (x, y, z) est représenté par un point du plan de coordonnées (x", z") telles que :

  • x" = x + k·cos α·y ;
  • z" = z + k·sin α·y.

La matrice de transformation est donc

P = \begin{pmatrix} 1 & k \cdot \cos \alpha & 0 \\ 0 & k \cdot \sin \alpha & 1 \end{pmatrix}

Pour un angle de 45° et un rapport de 0,5, on a :

  • x" = x + 0,35·y ;
  • z" = z + 0,35·y.

Notes et références

  1. ↑ Édouard Bahr, Le Dessin technique de la tuyauterie industrielle, Editions TECHNIP, 1991, p 5
  2. ↑ Certains ouvrages imposent un angle de 45 ° et un rapport de 0,5. C'est la cas , par exemple, du Guide du Dessinateur Industriel d'André Chevalier , Hachette Technique
  3. ↑ Étymologie pour le prof de maths ; Perspective cavalière
  4. ↑ Les origines des notations mathématiques

Liens externes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Perspective cavalière de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Perspective cavaliere — Perspective cavalière Parties de fortification en perspective cavalière (Cyclopaedia vol. 1, 1728) …   Wikipédia en Français

  • Perspective cavalière ou parallèle — ● Perspective cavalière ou parallèle système de représentation où le point de vue est situé à l infini (les lignes parallèles qui fuient restent non convergentes) …   Encyclopédie Universelle

  • PERSPECTIVE — Par sa situation au carrefour de la science, de la culture humaniste et de la pratique artistique, la perspective, comme tout autre thème interdisciplinaire, échappe à un traitement conceptuel univoque. Dans son acception technique, le terme… …   Encyclopédie Universelle

  • Perspective axonometrique — Perspective axonométrique commode en perspective axonométrique Dans un certain nombre de situations, et notamment en dessin technique, le dessin est la représentation d objets réels. Le lecteur du dessin doit pouvoir se représenter la pièce en… …   Wikipédia en Français

  • Perspective dimétrique — Perspective axonométrique commode en perspective axonométrique Dans un certain nombre de situations, et notamment en dessin technique, le dessin est la représentation d objets réels. Le lecteur du dessin doit pouvoir se représenter la pièce en… …   Wikipédia en Français

  • Perspective (representation) — Perspective (représentation) Pour les articles homonymes, voir Perspective. Jeu de perspective entre La Vierge à l’enfant avec l’ange musicien de G …   Wikipédia en Français

  • Perspective isometrique — Perspective isométrique Plan d une fortification en perspective isométrique La perspective isométrique est une méthode de représentation en perspective dans laquelle les trois directions de l espace sont représentées avec la même importance, d où …   Wikipédia en Français

  • Perspective axonométrique — Une commode en perspective axonométrique. En dessin technique et en architecture, une perspective parallèle, ou perspective cylindrique ou perspective axonométrique est une forme de représentation en dimension deux d objets en dimension trois qui …   Wikipédia en Français

  • Perspective (représentation) — Pour les articles homonymes, voir Perspective. Jeu de perspective entre La Vierge à l’enfant avec l’ange musicien de Giovanni Bellini et l église San Zaccaria de …   Wikipédia en Français

  • Perspective conique — Pour les articles homonymes, voir perspective. La perspective conique est le mode de représentation du monde environnant qui imite le mieux celui d une photographie. La découverte des règles qui en gouvernent l élaboration a été faite en Italie… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”