- Partie linéaire
-
Application affine
C’est Euler, en 1748, qui est à l’origine du terme « transformation affine », car dit-il, « deux courbes images l’une de l’autre par une telle transformation présentent entre elles une certaine affinité ».
De nos jours, une application affine est une application entre deux espaces affines qui préserve la structure affine, c'est-à-dire qui envoie les droites, plans, espaces,... en des droites, plans, espaces, ... tout en préservant la notion de parallélisme.
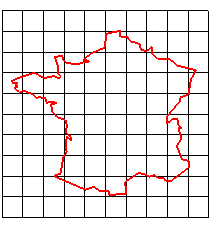 ➪
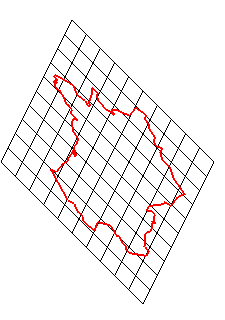
➪ 
Sommaire
Définition et premières propriétés
Une application
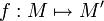 d'un espace affine
d'un espace affine  vers un espace affine
vers un espace affine 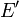 est dite affine s'il existe une application linéaire
est dite affine s'il existe une application linéaire 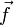 de l'espace vectoriel
de l'espace vectoriel 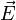 associé à
associé à  vers l'espace vectoriel
vers l'espace vectoriel 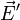 associé à
associé à 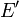 , appelée la partie linéaire de
, appelée la partie linéaire de  , satisfaisant :
, satisfaisant :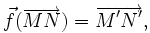
pour tous points
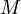 et
et 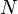 de
de  .
.Une application affine est donc déterminée par la donnée d'un couple de points homologues
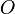 et
et 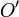 et de sa partie linéaire :
et de sa partie linéaire :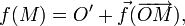
Si E est de dimension n, elle est également déterminée par la donnée de n + 1 points formant un repère affine et de leurs images.
Définitions équivalentes :
- Application linéaire d'un vectorialisé
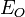 de
de  , vers un vectorialisé
, vers un vectorialisé 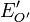 de
de 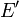 .
. - Application conservant les barycentres.
Deux sous-affines parallèles dans
 ont pour image des sous-espaces affines parallèles dans
ont pour image des sous-espaces affines parallèles dans 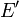 (les applications affines préservent le parallélisme).
(les applications affines préservent le parallélisme).Une application affine d'un espace affine dans lui même est appelée endomorphisme affine, et un endomorphisme bijectif est appelé un automorphisme, ou plus couramment une transformation affine. Les transformations affines forment un groupe, appelé le groupe affine de
 , noté
, noté 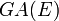
Exemples d'endomorphismes affines
- les translations (caractérisation : partie linéaire = l'identité).
- les symétries centrales (caractérisation : partie linéaire = - l'identité) .
- plus généralement, les homothéties (affines) (caractérisation : partie linéaire = une homothétie (vectorielle), uniquement dans le cas d'un rapport différent de 1)
- les symétries (affines) (caractérisation : au moins un point fixe et partie linéaire = une involution, ou application affine de carré égal à l'identité)
- les projections (affines) (caractérisation : au moins un point fixe et partie linéaire = un projecteur, ou application affine de carré égal à elle-même)
- les affinités, comprenant toutes les précédentes
- les transvections
- dans le cas euclidien : les isométries et similitudes
Points fixes des endomorphismes affines
Les points fixes jouent un rôle important pour les endomorphismes affines car un endomorphisme affine ayant un point fixe
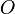 est "moralement" une application linéaire (du vectorialisé
est "moralement" une application linéaire (du vectorialisé 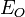 ).
).S'il est non vide, l'ensemble des points fixes de l'endomorphisme affine
 est un sous-espace affine de direction
est un sous-espace affine de direction 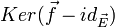 : de plus si
: de plus si 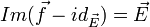 , alors il existe au moins un point invariant pour
, alors il existe au moins un point invariant pour  . On en déduit qu'en dimension finie si la partie linéaire de
. On en déduit qu'en dimension finie si la partie linéaire de  a un unique vecteur invariant, alors
a un unique vecteur invariant, alors  a un unique point invariant.
a un unique point invariant.D'autre part, pour un endomorphisme affine
 sans point fixe, on trouve facilement une translation qui, composée avec
sans point fixe, on trouve facilement une translation qui, composée avec  , donne une application ayant un point fixe, mais cette translation ne commute pas avec
, donne une application ayant un point fixe, mais cette translation ne commute pas avec  en général. Cependant, si
en général. Cependant, si 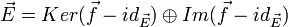 , il existe un unique vecteur
, il existe un unique vecteur 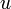 et une unique application affine
et une unique application affine 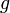 ayant un point fixe telle que
ayant un point fixe telle que 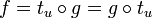 ; c'est le cas par exemple des symétries glissées.
; c'est le cas par exemple des symétries glissées.Transformation affine comme cas particulier d'homographie
L'espace affine
 peut être complété par un hyperplan à l'infini
peut être complété par un hyperplan à l'infini 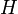 en un espace projectif
en un espace projectif 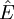 ; une transformation affine
; une transformation affine  de E\, se prolonge alors de façon unique en une transformation projective, ou homographie de
de E\, se prolonge alors de façon unique en une transformation projective, ou homographie de 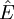 , laissant
, laissant 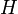 invariant.
invariant.Réciproquement, toute homographie laissant un hyperplan invariant se restreint dans le complémentaire de cet hyperplan à une transformation affine.
En raccourci, les transformations affines sont les homographies ayant un hyperplan invariant, et on en déduit que le groupe affine est un sous-groupe du groupe projectif.
Les applications affines dans
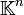
Les applications affines dans
 sont exactement les applications
sont exactement les applications 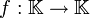 de la forme
de la forme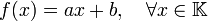
avec
 et
et  deux réels quelconques. L'application linéaire qui lui est associée est
deux réels quelconques. L'application linéaire qui lui est associée est 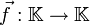 avec
avec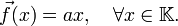
De façon plus générale, une application affine
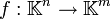 est une application de la forme
est une application de la forme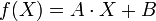
où
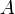 est une matrice
est une matrice 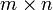 et
et 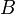 une matrice
une matrice 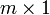 . L'application linéaire associée est
. L'application linéaire associée est 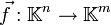 définie par
définie par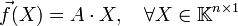
Translations et affinités dans
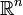
- L'application T est une translation de vecteur
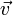 si et seulement si
si et seulement si

- L'application T est une affinité de coefficient k si et seulement si la matrice A n'admet pour valeurs propres que 1 et k, et si les espaces propres associés sont supplémentaires (la somme de leurs dimensions est égale à n, l'une d'elle pouvant être nulle).
- En particulier, si k = 0, l'affinité est une projection (la matrice A représente une projection vectorielle dans
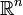 ).
). - Si k = − 1, alors l'affinité est une symétrie (la matrice A représente une symétrie vectorielle).
- Si A n'admet qu'une seule valeur propre
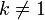 de multiplicité n, alors T est une homothétie de rapport k et de centre P qui est l'unique point solution du système linéaire
de multiplicité n, alors T est une homothétie de rapport k et de centre P qui est l'unique point solution du système linéaire
- En particulier, si k = 0, l'affinité est une projection (la matrice A représente une projection vectorielle dans
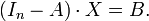
Caractérisations géométriques des applications affines
On suppose dans ce paragraphe que
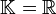 et que les espaces sont de dimension finie.
et que les espaces sont de dimension finie.1) Les applications affines sont les applications conservant les barycentres.
Ceci vaut aussi bien pour les barycentres de familles finies que des centres d'inertie de parties munies de fonctions de masse ; le centre d'inertie d'un objet aura pour image par une application affine le centre d'inertie de l'objet image.
Grâce à l'associativité, on peut réduire la condition au fait de conserver les barycentres de deux points, mais on ne peut aller jusqu'à la conservation des milieux : les applications conservant les milieux sont les applications
 -affines, et on peut construire par l'axiome du choix des applications
-affines, et on peut construire par l'axiome du choix des applications  -affines non
-affines non  -affines.
-affines.Cependant, on peut montrer que
2) Les applications affines sont les applications continues conservant les milieux.
Remarque : la propriété de conservation des milieux équivaut à celle de conservation des parallélogrammes.
3) En dimension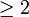 , les transformations affines sont les bijections transformant une droite en une droite.
, les transformations affines sont les bijections transformant une droite en une droite.Ceci est une version du théorème fondamental de la géométrie affine. Il est remarquable qu'il n'y ait pas besoin de préciser que deux droites parallèles ont des images parallèles.
On peut même restreindre la caractérisation à :
4) En dimension
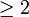 , les transformations affines sont les bijections transformant 3 points alignés en 3 points alignés.
, les transformations affines sont les bijections transformant 3 points alignés en 3 points alignés.Voir la page théorème fondamental de la géométrie affine pour plus de précisions.
Voir aussi
- Les espaces affines
- Portail des mathématiques
Catégories : Géométrie affine | Transformation géométrique - Application linéaire d'un vectorialisé
Wikimedia Foundation. 2010.
