Paradoxe de selleri

Le paradoxe de Selleri décrit une situation où, en raisonnant dans un repère tournant, on montre que les transformations des coordonnées doivent obéir aux transformations de Galilée. La situation est paradoxale dans le sens que l'on ne remet pas initialement en cause les postulats de la relativité restreinte qui permettent de montrer que les transformations des coordonnées obéissent aux transformations de Lorentz. On part d'une situation simple et on effectue un raisonnement apparemment sans faille qui conduit à invalider ces postulats de la relativité (invariance de la vitesse de la lumière et équivalence des repères).

Soit un disque en rotation dans le repère inertiel R et un observateur O' situé au borde de ce disque (et tournant avec lui). Le repère R' (tournant) est le repère attaché à cet observateur. Soit deux signaux envoyés avec la vitesse c (mesuré dans le repère R) le long de la circonférence dans chaque sens.

Alors, l'étude de l'effet Sagnac montre que la vitesse des signaux lumineux dans le repère en rotation R' est donnée par :

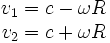
où ω est la vitesse angulaire de rotation du disque.

Ces formules peuvent s'exprimer en fonction de la vitesse tangentielle V de O' :

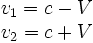
Avec la vitesse tangentielle V = Rω.

Ces formules ne dépendent pas du rayon R du cercle mais uniquement de la vitesse de O'. Nous pouvons donc faire tendre le rayon vers l'infini et le moment angulaire vers zéro de manière à garder la vitesse de O' constante.

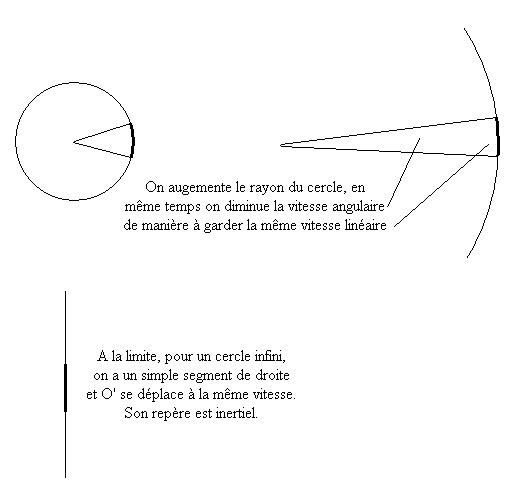
Dans ce cas, le repère R' tend vers un repère inertiel se déplaçant à vitesse V par rapport à R. La courbure de la trajectoire tend vers zéro et la force centrifuge aussi.

En effet :

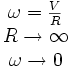
On peut faire tendre simultanément R vers l'infini et ω vers zéro de manière à garder V constant. Les formules déduites des sections précédentes pour la vitesse restent inchangées.

Par exemple en faisant tendre le paramètre λ vers l'infini avec :

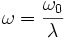et R = R₀λ

où ω₀ et R₀ sont des constantes, on a :

V = ω₀R₀ et

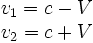
quelle que soit la valeur de λ.

À la limite 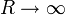, la trajectoire de O' devient une droite à vitesse V constante, R' est donc inertiel.

Mais la formule d'addition des vitesses trouvée et donnée ci-dessus reste constamment valable, donc la vitesse de la lumière reste anisotrope dans R'. Même lorsqu'il est un repère inertiel ! Or nous savons que la vitesse n'est pas anisotrope dans un repère inertiel (c'est le principe de relativité). C'est le paradoxe de Selleri.

Pour celui qui trouverait absurde de faire tendre le cercle vers un cercle infini, il suffit de considérer uniquement la portion de trajectoire de O'. C'est un arc de cercle quasiment plat, pratiquement un segment de ligne droite.

On pourrait invoquer que dès que le cercle devient trop grand (par rapport à l'univers ou par rapport à l'univers observable), c’est-à-dire lorsqu'on est obligé de considérer uniquement l'arc de cercle, alors la lumière ne pouvant plus faire « le tour », la vitesse n'est plus anisotrope.

Mais cela continue à poser des problèmes.

• Il est difficile de justifier le comportement local (vitesse anisotrope pour R' pour les rayons lumineux partant dans un sens ou l'autre) par une possibilité à grande échelle (la possibilité ou pas pour le rayon lumineux de faire un tour complet et revenir en O').
  Comment le fait qu'un rayon lumineux puisse emprunter tel ou tel chemin en fonction des circonstances pourrait-il influencer la physique locale, c’est-à-dire la vitesse d'un rayon lumineux sans qu'il ait à faire le tour ?
  C’est-à-dire, comment le signal lumineux pourrait-il "savoir" que s'il continuait, il aurait ou pas la possibilité de faire ce tour et doit donc « adapter » sa vitesse en fonction ?
• On a une discontinuité. Que la transition se fasse quand le cercle est « trop grand » (quelle que soit cette taille « maximale ») ou quand le repère est inertiel (par passage à la limite), on a un brusque changement dans la vitesse de la lumière qui passe, par exemple, de c + V à c.
  Rappelons que les transformations de Galilée sont incompatibles avec l'invariance de la vitesse de la lumière, même sur un aller-retour. Cette discontinuité (passage de l'addition galiléenne des vitesses comme ci-dessus à la composition relativiste des vitesses) est donc inévitable et assez incompréhensible.
• Nous n'avons pas d'explication de l'universalité de l'effet Sagnac.

Comme nous le rappelons ci-dessus, les transformations de Galilée (et l'addition des vitesses qui va avec) sont incompatibles avec les données expérimentales. Retrouver à partir d'un raisonnement apparemment « sans faille » que l'on doit avoir une addition galiléenne des vitesses dans un repère inertiel est donc réellement paradoxal.

C'est un sérieux problème qui montre bien que « quelque chose » cloche dans nos raisonnements. Mais quoi ?

La solution réside dans une analyse plus rigoureuse de la situation des repères tournants dans le cadre de la relativité restreinte.

Voir aussi

• L'effet Sagnac
• Le paradoxe d'Ehrenfest
• La synchronisation dans les repères tournants
• Le calcul de l'effet Sagnac en relativité restreinte
• La géométrie de l'espace-temps dans les repères tournants
• Le paradoxe des jumeaux et l'effet Sagnac
• Les espaces compacts
• Le paradoxe des jumeaux dans les espaces compacts
• La relativité restreinte
• La relativité générale
• Le principe de relativité
• Le paradoxe des jumeaux

Bibliographie

• Théorie de la Relativité Restreinte, V. Ougarov, Deuxième Edition, Editions Mir, Moscou, Traduction française Editions Mir, 1979.

Liens externes

• The relativistic Sagnac effect : two derivations par Guido Rizzi et Matteo Luca Ruggiero

• Portail de la physique