Parabole de sûreté

Parabole de sûreté
Enveloppe de sûreté (en rouge) des trajectoires paraboliques. Ces dernières ont leur sommet sur une même ellipse (en bleu).

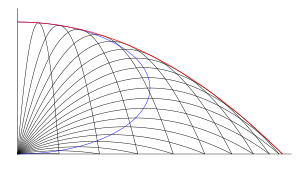
En physique et en balistique, on désigne par parabole de sûreté la courbe enveloppe de toutes les trajectoires paraboliques possibles d'un projectile lancé depuis un point donné avec une vitesse donnée dans un plan vertical d'azimut fixé[1]. Nul point extérieur à cette courbe ne peut être atteint par un projectile : la zone est « sûre », d'où le nom de la courbe.

En coordonnées cartésiennes, cette parabole est décrite par l'équation :

z = h - \frac{x^2}{4h}

où h = \tfrac{V_0^2}{2g} désigne l'altitude maximale pouvant être atteinte.

Sommaire

Équations décrivant la parabole de sûreté

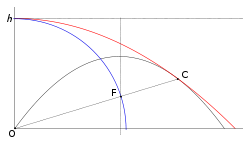Parabole de sûreté (en rouge) de trajectoires paraboliques (en noir) dont une seule est tracée. En bleu, lieu des foyers F des trajectoires paraboliques. C est le point de Torricelli de la trajectoire considérée. La droite (OC) passe par le foyer F. La droite z = h est la directrice commune à toutes les trajectoires paraboliques.

Soit un boulet B, lancé à une vitesse initiale V0 à partir du point O, tombant dans le vide, dans un champ de pesanteur uniforme g. Sa trajectoire, dans le plan vertical (O,V0,g), est parabolique :

\overrightarrow{\rm OB} = \frac {1}{2} t^2 \vec{g} + t \vec{V_0}

Et l'équation cartésienne de cette parabole est :

z(x) = - \frac {x^2 } {4h}\left(1+ \tan^2(A)\right) + x \tan(A)

en notant A l'angle de tir (angle entre le vecteur V0 et l'horizontale), et h = \tfrac{V_0^2}{2g}, l'altitude maximale atteinte lors d'un tir vertical.

Pour atteindre le point M(x0,z0), l'artilleur devra choisir la hausse A du canon, c'est-à-dire tan(A), telle que :

z_0 = - \frac{x_0^2}{4h} \left(1+ \tan^2(A)\right) + x_0 \tan(A)

Cette équation étant du second degré en tan(A), il apparaît donc qu'il y a deux solutions, une solution double ou pas de solution, selon que le discriminant Δ est positif, nul ou négatif. Dans le cas limite, le point M est dit se trouver sur la courbe de sûreté (C). On a

\Delta = 0 =x_0^2- 4\left(z_0+ \frac{x_0^2}{4h}\right)\frac{x_0^2}{4h}

qui se simplifie et donne l'équation d'une parabole dite de sûreté :

z_0 = h - \frac{x_0^2}{4h}

On obtient z0 = 0 lorsque x0 = 2h, distance appelée portée maximale horizontale.

On peut montrer que la trajectoire de chute contacte tangentiellement la courbe (C) en un point C, dit de Torricelli, tel que (OC) est corde focale de la trajectoire parabolique. Ce fait a été remarqué par Torricelli en 1640[réf. nécessaire] et lui a permis de déterminer géométriquement la nature de l'enveloppe.

Avantage de la citadelle

Un avantage de la citadelle est que ses canons se trouvent à une altitude a = OA au-dessus de la plaine. Les boulets vont pouvoir atteindre un point P tel que x = OP > 2h. Plus précisément, x est tel que z = -a = h - \tfrac{x^2}{4h}, soit x = 2√h(h+a). Par le théorème de Pythagore, AP = 2h + a : la distance entre la citadelle A et le point P de portée maximale est donc la somme de l'altitude a avec la portée maximale 2h lorsque le tir est effectué avec une altitude nulle[2]. Ce résultat étonne souvent par sa simplicité. Similairement, les assaillants devront se rapprocher (il suffit de changer a en -a).

  • Exemple : pour h = 100 m, la portée des canons est de 200 m. Une citadelle située à une altitude a = 50 m aura une portée AP = 250 m. Inversement, les assaillants devront s'approcher à 150 m pour pouvoir atteindre la citadelle.
  • Avantage de l'avant-poste : Soit un avant-poste de hauteur O'A' = a' par rapport à la citadelle, et situé à une distance OO' = b de la citadelle. Le même genre de raisonnement conduit à ce constat simple : la hauteur effective est alors a' + b + a.

Notes et références

  1. ↑ Par rotation autour de la verticale, on obtient un paraboloïde de révolution qui enveloppe toutes les trajectoires paraboliques possibles depuis un point donné avec une vitesse donnée
  2. ↑ et l'angle de tir est \frac{\pi}{4} - \tfrac{1}{2} \arcsin \tfrac{a}{a + 2h}

Voir aussi



Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Parabole de sûreté de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Parabole de surete — Parabole de sûreté Soit un boulet B (lancé à une vitesse initiale Vo), tombant dans le vide, dans un champ de pesanteur uniforme g. Sa trajectoire sera dans le plan vertical (O, Vo, g). Selon la célèbre loi de la chute libre énoncée en 1602 par… …   Wikipédia en Français

  • Parabole — Pour les articles homonymes, voir Parabole (homonymie). Une parabole La parabole est l intersection d un plan avec un cône de révolution lorsque le plan est par …   Wikipédia en Français

  • Ellipse de sûreté — En balistique extérieure, pour des distances importantes du projectile, la notion d ellipse de sûreté généralise celle de parabole de sûreté. Description On considère un modèle de Terre sphérique de centre T et une base B de lancement. On pose TB …   Wikipédia en Français

  • Evangelista Torricelli — Pour les articles homonymes, voir Evangelista et Torricelli. Torricelli inventant le baromètre à mercure Evangelista Torricelli (né le 15 octobre 1608 à Faenza, en Émi …   Wikipédia en Français

  • Toriccelli — Evangelista Torricelli Torricelli inventant le baromètre à mercure Evangelista Torricelli (né le 15 octobre 1608 à Faenza, en Émilie Romagne mort le 25 octobre 1647 à Florence) est un physicien et un mathématicien italien du …   Wikipédia en Français

  • Balistique Extérieure — La balistique extérieure est la branche de la balistique qui étudie le vol libre des projectiles sans propulsion interne. Le cas d application le plus important est l étude de la trajectoire des balles ou obus tirés par une arme à feu après qu… …   Wikipédia en Français

  • Balistique exterieure — Balistique extérieure La balistique extérieure est la branche de la balistique qui étudie le vol libre des projectiles sans propulsion interne. Le cas d application le plus important est l étude de la trajectoire des balles ou obus tirés par une… …   Wikipédia en Français

  • Trajectoire parabolique — Une trajectoire est dite parabolique si le mouvement d un corps dans l espace décrit une parabole. Le mouvement parabolique s effectue lorsqu un projectile est soumis à une vitesse initiale et à la seule accélération de la pesanteur. Un exemple… …   Wikipédia en Français

  • Chute Libre (Physique) — Pour les articles homonymes, voir Chute libre. Une chute libre est un mouvement accéléré sous le seul effet de la pesanteur. On distingue la simple chute dans un champ de pesanteur uniforme au voisinage de la Terre (Galilée, 1605), et la chute… …   Wikipédia en Français

  • Chute libre (physique) — Pour les articles homonymes, voir Chute libre. Une chute libre est un mouvement sous le seul effet de la pesanteur. On distingue la simple chute dans un champ de pesanteur uniforme au voisinage de la Terre (Galilée, 1605), et la chute céleste… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”