- Oscillateur paramétrique optique
-
Un oscillateur paramétrique optique (OPO) est une source de lumière cohérente et monochromatique. À partir d'une onde laser de pompe de fréquence ωp, un OPO produit deux ondes de fréquences inférieures : le signal à ωs et le complémentaire à ωc (parfois appelé idler). La conservation de l'énergie impose que ωp = ωs+ωc. La conversion de fréquence de la pompe vers les deux ondes générées se fait au travers d'une interaction optique non-linéaire. La lumière émise par les OPO peut s'étendre de l'ultra-violet au lointain infrarouge, de façon continue ou selon des impulsions de durées variables (de la microseconde à la femtoseconde).
Les OPO sont principalement utilisés pour produire des longueurs d'onde là où les lasers font défaut, où lorsqu'une très grande accordabilité est nécessaire. À défaut de pouvoir être encore miniaturisés comme les diodes lasers, ils n'ont trouvé à ce jour que très peu d'applications grand public. En revanche, ils sont prisés par la défense pour des applications de lidar ou de brouillage, car ils permettent un large accès au domaine infrarouge, en particulier dans les bandes de transmission atmosphérique. Ils trouvent également un intérêt dans les applications scientifiques, où une longueur d'onde bien précise est nécessaire (telle que la manipulation cohérente d'atomes pour l'information quantique), ou lorsque une grande accordabilité est requise (spectroscopie).
Principe général
Un OPO est constitué de deux éléments essentiels :
- un milieu non-linéaire, à l'origine de la conversion de fréquence effectuée par l'OPO. Ce milieu créé un gain non-linéaire pour les ondes signal et complémentaire. Ce milieu est souvent un cristal non-linéaire, comme le niobiate de lithium ;
- une cavité optique, généralement constituée de deux miroirs hautement réfléchissants (dans le cas continu) situés de part et d'autre du milieu amplificateur. Le rôle de la cavité optique est de faire osciller le rayonnement, et donc de permettre son amplification par passages successifs dans le milieu non-linéaire. D'autre part, cette cavité introduit nécessairement des pertes pour les ondes oscillantes.
 Schéma de principe d'un oscillateur paramétrique optique, cas d'un OPO simplement résonnant
Schéma de principe d'un oscillateur paramétrique optique, cas d'un OPO simplement résonnantÀ faible puissance de pompe, le gain est trop faible par rapport aux pertes : il n'y a pas d'oscillation. Au-delà d'une certaine puissance de pompe, appelée seuil d'oscillation, le gain dépasse les pertes et l'amplification progressive des ondes générées est possible. Lorsque la puissance des ondes oscillantes devient importante, le gain diminue. À l'état stationnaire, gain et pertes sur un aller-retour de cavité se compensent exactement. Le seuil d'oscillation peut aller de quelques dizaines de milliwatts à quelques watts, selon le matériau non-linéaire, les pertes de la cavité optique, la fréquence de l'onde de pompe, et la durée des impulsions de pompe.
En transférant une partie de son énergie aux ondes signal et complémentaire, la pompe est atténuée au cours de l'interaction : on parle de dépeuplement de la pompe. À forte puissance de pompe il peut arriver que la pompe soit entièrement dépeuplée. Le signal et le complémentaire se recombinent alors pour refaire de la pompe. Cet effet, caractéristique de la réversibilité de l'interaction non-linéaire, est appelé saturation et est généralement non souhaitable dans un OPO.
Dans le cas d'un SROPO (OPO simplement résonnant), si le signal est l'onde résonante, c'est l'onde complémentaire qui est extraite de la cavité et vice-versa. Comme le signal atteint une amplitude très importante dans la cavité, il permet la production d'une onde complémentaire puissante. Ce système est différent de celui du laser où l'onde résonante est également l'onde extraite, ce qui nécessite un compromis sur la réflectivité du miroir de sortie. Des puissances moyennes de quelques watts peuvent être extraites de certains OPO.
Une des caractéristiques principales d'un OPO est son accordabilité. En effet, les fréquences des ondes générées peuvent être ajustées de manière continue en changeant l'accord de phase entre les trois ondes (voir ci-dessous). En pratique, cela revient à tourner un cristal non-linéaire autour d'un axe particulier, ou bien à changer sa température. Lorsqu'un accord de phase de ce type n'est pas possible, on utilise le quasi-accord de phase, qui nécessite des cristaux possédant un réseau, c'est-dire dont les propriétés non-linéaires ont été modifiées périodiquement. L'accordabilité se fait alors en modifiant la période de retournement, soit en se plaçant sur un réseau différent pour les cristaux multi-réseaux, soit en changeant la température.
Une autre caractéristique particulière des OPO est la cohérence et la largeur spectrale des ondes générées. En effet, un OPO ne peut être pompé que par un faisceau optique cohérent, en pratique celui d'un laser ou d'un autre OPO, et le transfert d'énergie se fait de façon instantanée. La pompe transfère donc une partie de sa phase et de ses caractéristiques spectrales aux ondes générées. Dans un OPO simplement résonnant, l'onde qui oscille peut ainsi posséder une largeur spectrale très fine (quelques kHz), les impuretés étant transmises à la deuxième onde. D'autre part, en dessous ou près du seuil d'oscillation, les ondes générées ont des propriétés quantiques intéressantes...
Les OPO sont souvent utilisés pour produire des longueurs d'onde inaccessibles avec les lasers existants, en particulier dans l'infrarouge moyen (vers 4 μm) ou lointain (vers 10 μm). Les OPO sont également intéressants lorsque la longueur d'onde doit pouvoir être changée en temps réel sur une large gamme (10 nm ou plus).
Génération de la lumière dans un OPO
 Génération paramétrique du signal et du complémentaire à partir de la pompe dans un milieu non-linéaire. Le processus met en jeu des niveaux virtuels. Le niveau intermédiaire a donc une position variable entre les deux niveaux extrêmes.
Génération paramétrique du signal et du complémentaire à partir de la pompe dans un milieu non-linéaire. Le processus met en jeu des niveaux virtuels. Le niveau intermédiaire a donc une position variable entre les deux niveaux extrêmes.Lorsque le milieu non-linéaire est éclairé par un faisceau de lumière cohérente de fréquence ωp, appelé faisceau de pompe, deux autres faisceaux sont produits : le faisceau signal de fréquence ωs et le faisceau complémentaire de fréquence ωc. Il n'existe pas de convention générale pour définir le signal par rapport au complémentaire (même si dans la majorité des publications sur le sujet le signal a la longueur d'onde la plus courte des deux). Les fréquences signal et complémentaire sont forcément inférieures à la fréquence de pompe, et doivent impérativement satisfaire la relation suivante :
Au cours de la propagation dans le milieu non-linéaire, l'énergie du faisceau pompe est transférée en faveur des faisceaux signal et complémentaire, si bien qu'on parle aussi de mélange ou de couplage à trois ondes. Le milieu non-linéaire se comporte donc comme un convertisseur de fréquence optique. Comme pour tous les phénomènes d'optique non-linéaire, ce phénomène n'apparait qu'à des densités de puissance lumineuse assez importantes, ce qui nécessite l'emploi d'un laser.
On décrit parfois ce processus en termes de photons (approche corpusculaire). Ainsi, chaque photon de pompe « se scinde » en deux autres photons. Si on se rappelle que l'énergie d'un photon est
 , où
, où  est la constante de Planck, la relation précédente ne traduit rien d'autre que la conservation de l'énergie. Ici, il ne faut pas confondre l'énergie individuelle des photons, qui traduit une fréquence, et celle des faisceaux en entier, qui traduit le flux lumineux (ou débit de photons).
est la constante de Planck, la relation précédente ne traduit rien d'autre que la conservation de l'énergie. Ici, il ne faut pas confondre l'énergie individuelle des photons, qui traduit une fréquence, et celle des faisceaux en entier, qui traduit le flux lumineux (ou débit de photons).Cependant, cette relation seule n'impose pas les valeurs individuelles des fréquences signal et complémentaire, si bien qu'un nombre infini de possibilités semble exister. En réalité, les trois ondes mises en jeu doivent également respecter la relation d'accord de phase.
Comment fonctionne un OPO : l'accord de phase
Importance de l'accord de phase
 Schéma de l'accord de phase lors de la génération paramétrique
Schéma de l'accord de phase lors de la génération paramétriqueLa conversion de la pompe vers les faisceaux générés n'est efficace que si les vitesses de phase v des ondes respectent la relation suivante :
La signification de cette relation apparaît plus clairement dans le cas particulier de la dégénérescence, pour lequel signal et complémentaire sont de fréquences identiques, ωs = ωc = ωp/2 :
Sans cette condition, les ondes générées au cours de la propagation dans le milieu non-linéaire se déphasent et finissent par interférer de façon destructive : la puissance résultante est très faible. Lorsque l'accord de phase est réalisé, les ondes interfèrent de façon constructive, et la puissance générée varie comme le carré de la longueur du milieu non-linéaire :
où g est le gain paramétrique, proportionnel à la non-linéarité du milieu et à l'amplitude de l'onde de pompe.
Cette relation d'accord de phase peut également s'écrire sous une forme plus générale, en fonction des vecteurs d'onde :
Si on se rappelle que l'impulsion d'un photon est
 , la relation précédente ne traduit rien d'autre que la conservation de la quantité de mouvement des photons. Comme il s'agit d'une relation vectorielle, cela signifie qu'il peut exister des accords de phase non colinéaires, c'est-à-dire pour des faisceaux pompe, signal et complémentaire se propageant dans des directions différentes.
, la relation précédente ne traduit rien d'autre que la conservation de la quantité de mouvement des photons. Comme il s'agit d'une relation vectorielle, cela signifie qu'il peut exister des accords de phase non colinéaires, c'est-à-dire pour des faisceaux pompe, signal et complémentaire se propageant dans des directions différentes.Contrairement à la conservation de l'énergie, l'accord de phase est une condition qui ne se réalise pas toute seule. En effet, dans le milieu non-linéaire, les vitesses de phase des trois ondes sont différentes, car leurs fréquences sont différentes. Cette propriété générale des milieux matériels est la dispersion. Le rôle de la dispersion apparait plus clairement si la relation d'accord de phase est réécrite en introduisant les indices de réfraction ou indices optiques n des ondes,
 :
:Cette égalité semble impossible puisque
 et qu'en plus les trois ondes doivent respecter la conservation de l'énergie,
et qu'en plus les trois ondes doivent respecter la conservation de l'énergie,  . En réalité, dans certains matériaux, appelés biréfringents, ou anisotropes, l'indice de réfraction dépend également de la polarisation. Grâce à ce degré de liberté supplémentaire, il est possible de réaliser l'accord de phase entre des ondes de fréquences différentes, à condition que leurs polarisations soient judicieusement choisies. Dans les milieux non-linéaires isotropes en revanche, ce type d'accord de phase n'est pas possible : c'est la technique du quasi-accord de phase qui est alors utilisée.
. En réalité, dans certains matériaux, appelés biréfringents, ou anisotropes, l'indice de réfraction dépend également de la polarisation. Grâce à ce degré de liberté supplémentaire, il est possible de réaliser l'accord de phase entre des ondes de fréquences différentes, à condition que leurs polarisations soient judicieusement choisies. Dans les milieux non-linéaires isotropes en revanche, ce type d'accord de phase n'est pas possible : c'est la technique du quasi-accord de phase qui est alors utilisée.La découverte de l'accord de phase par biréfringence est généralement attribuée à Joseph A. Giordmaine et Paul D. Maker en 1962. Le quasi-accord de phase a été imaginé par Nicolaas Bloembergen et John Armstrong en 1962 ainsi qu'indépendamment par P. A. Franken et J. F. Ward la même année.
Accord de phase par biréfringence
 Accord de phase par biréfringence pour un cristal uniaxe positif (ne > no) dans le cas dégénéré (ωs = ωi = ωp/2)
Accord de phase par biréfringence pour un cristal uniaxe positif (ne > no) dans le cas dégénéré (ωs = ωi = ωp/2)Pour comprendre l'accord de phase par biréfringence, prenons l'exemple du cristal non-linéaire de Beta Borate de Baryum β-BaB2O4 (BBO). Ce cristal possède deux indices optiques selon la polarisation de la lumière : un indice ordinaire no(ω) pour une certaine polarisation O de la lumière, et un indice extraordinaire ne(θ, ω) pour la polarisation E perpendiculaire. L'indice ordinaire ne dépend pas de la direction de propagation θ des ondes lumineuses, exactement comme dans un cristal isotrope. L'indice extraordinaire, lui, en dépend. Dans ce cristal, si l'onde pompe est polarisée E et se propage avec un certain angle θ, elle peut être convertie efficacement en une onde signal et une onde complémentaire toutes deux polarisées O. On note ce processus de la manière suivante :
 . La relation d'accord de phase est donc possible et s'écrit dans ce cas :
. La relation d'accord de phase est donc possible et s'écrit dans ce cas :Dans le cas simple de la dégénérescence, réaliser l'accord de phase signifie trouver la direction de propagation θ telle que l'onde pompe extraordinaire ait le même indice (i.e. la même vitesse de phase) que l'onde ordinaire générée :
De manière générale, on distingue les accord de phase de type I, où signal et idler sont polarisés de la même manière :
et les accords de phase de type II où ces deux ondes ont leur polarisations croisées :
Ces deux types d'accords de phase peuvent exister simultanément dans un même cristal, et ont chacun des avantages et des inconvénients que nous ne détaillerons pas ici.
Cône de fluorescence paramétrique
Une autre façon de voir l'importance de l'angle de propagation des ondes dans les effets non-linéaires est ce qu'on appelle le cône de fluorescence paramétrique. Prenons le cas d'un cristal non-linéaire sans cavité optique, éclairé par une onde pompe de très forte intensité. Un accord de phase non colinéaire sera trouvé pour un couple de fréquences (ωs, ωc) correspondant à des directions de propagations des ondes (ks, kc), la direction de la pompe kp étant fixée. Un autre accord de phase existe pour un autre couple de fréquences (ωs', ωc') correspondant à des directions différentes (ks', kc'), et ainsi de suite. Il en résulte la génération de deux cônes de lumière superposés, un cône signal et un cône complémentaire. Pour une pompe ultraviolette à 351 nm, le cône signal est majoritairement dans le visible et le cône complémentaire dans l'infrarouge.
 Principe de l'accord de phase non-colinéaire pour la génération d'un cône de fluorescence paramétrique, et schéma correspondant pour une pompe laser ultra-violette.
Principe de l'accord de phase non-colinéaire pour la génération d'un cône de fluorescence paramétrique, et schéma correspondant pour une pompe laser ultra-violette.Quasi-accord de phase
Dans certains cas, il n'est pas possible de trouver un accord de phase par biréfringence pour les fréquences signal et complémentaire désirées. C'est le cas notamment des matériaux non-linéaires isotropes, comme l'arseniure de gallium GaAs. À défaut d'annuler exactement le désaccord de phase, il est parfois possible de le remettre à zéro périodiquement afin de garder les ondes en phase : c'est le quasi-accord de phase.
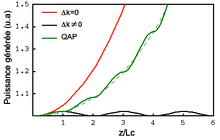
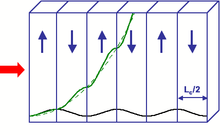 Schéma d'un cristal périodiquement retourné, et évolution de l'intensité générée par effet paramétrique avec (vert) ou sans (noir) retournement des domaines.
Schéma d'un cristal périodiquement retourné, et évolution de l'intensité générée par effet paramétrique avec (vert) ou sans (noir) retournement des domaines.
Pour cela, le signe de la non-linéarité du matériau doit être inversé toutes les longueurs de cohérence (voir figure ci-contre). Ceci équivaut à rajouter une phase de π au désaccord de phase, c'est-à-dire à renverser le sens du transfert d'énergie entre les ondes. Les interférences destructives qui ont normalement lieu à chaque longueur de cohérence sont supprimées, et la puissance des ondes générées peut croître continûment à la traversée du milieu non-linéaire (voir figure ci-contre). Cependant, l'efficacité est réduite d'un facteur (2/π)².
Si Λ est la période de retournement qui minimise le désaccord de phase, ce dernier s'écrit alors :
où
 est le vecteur du réseau formé par les domaines retournés.
est le vecteur du réseau formé par les domaines retournés.Il existe des variantes à ce quasi-accord de phase, comme l'inversion des domaines avec une période multiple de la longueur de cohérence, ou la modulation partielle de la non-linéarité, sinusoïdale par exemple. Le formalisme de Fourier permet de voir que toute modulation de la non-linéarité comportant une harmonique m du vecteur K est un quasi-accord de phase d'ordre m, plus ou moins efficace.
En plus de pouvoir remplacer l'accord de phase par biréfringence lorsque celui-ci n'est pas possible, le quasi-accord de phase possède un certain nombre d'avantages :
- Il n'est plus nécessaire d'avoir des ondes de polarisations croisées ;
- le décalage spatial (walk-off) entre les ondes est supprimé ;
- même pour les matériaux où il existe un accord de phase par biréfringence, le quasi-accord de phase peut permettre d'utiliser une direction de propagation dans laquelle la non-linéarité du matériau est plus importante.
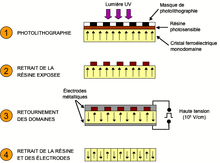
Pour réaliser l'inversion périodique de la non-linéarité, il existe plusieurs techniques. Dans les cristaux ferroélectriques comme le niobiate de lithium, le phosphate de potassium titanyl (KTP) et le phosphate de rubidium titanyl (RTP), le retournement se fait par l'application d'un champ électrique très intense (voir figure ci-contre). La période du réseau ainsi créé peut aller de quelques dizaines de μm à quelques μm, la résolution de cette technique ne permettant pas de descendre plus bas. Si une période plus petite est nécessaire, il est possible d'appliquer très localement le champ électrique par un microscope à force atomique (AFM), ou bien de provoquer le retournement des domaines par un faisceau d'électrons focalisé (analogue à celui d'un microscope électronique à balayage), ce qui permet de descendre en dessous de 1 μm. En revanche, avec ces techniques l'ouverture des cristaux est généralement limitée à quelques mm, ce qui limite le diamètre des faisceaux pouvant s'y propager, et limite l'acceptance angulaire du cristal.
Une autre technique consiste à découper des plaquettes dans le matériau non-linéaire, puis à les coller ensemble en alternant l'orientation. Pour certains matériaux comme l'arseniure de gallium, l'alternance se fait lors de la croissance par épitaxie, grâce à des motifs déposés sur le matériau.
Les matériaux ainsi inversés sont renommés en y ajoutant le préfixe anglo-saxon « PP » pour periodically poled. Un des premiers matériaux ainsi réalisés est le niobate de lihitum périodiquement retourné, ou PPLN, réalisé par l'équipe de Matuo Yamada des laboratoires Sony à la fin des années 1990, puis par celle de Martin Fejer de l'Université de Stanford. Le PP-GaAs est également intéressant car il est fortement non-linéaire.
La nature vectorielle de l'accord de phase a permis d'envisager des techniques d'accord de phase où la non-linéarité est modulée suivant deux directions de l'espace. Ce sont ainsi des réseaux à deux dimensions qui sont créés dans les cristaux non-linéaires.
Le quasi-accord de phase peut aussi être réalisé en remettant les ondes en phase périodiquement, sans inversion du signe de la non-linéarité. Le quasi-accord de phase de Fresnel exploite par exemple le déphasage dit de Fresnel subi par une onde lorsqu'elle se réfléchit à l'interface entre deux milieux. En faisant propager les ondes en zig-zag dans une plaquette de matériau, il est ainsi possible de rattraper le déphasage à chaque réflexion sur les bords de la plaquette. Mais ceci n'est possible que pour certains angles de propagation.
À noter qu'il existe également un quasi-accord de phase pour lequel c'est la dispersion qui est modulée, donc les valeurs des indices vus par les trois ondes.
Accord de phase par biréfringence de forme
Dans certains matériaux isotropes, il est possible de créer une biréfringence artificielle grâce à une structuration particulière du milieu. Deux ondes polarisées perpendiculairement voyant alors des indices effectifs de propagation différents, l'accord de phase devient possible. Cette technique a été surtout appliquée aux semiconducteurs, qui bénéficient des techniques de croissance et de structuration développées à l'origine pour la microélectronique. Par exemple, des guides alternant des couches de GaAs (indice élevé de ~ 3,5) et de Al(Ga)As oxydé (Alox d'indice faible ~ 1,6) ont été créés, permettant notamment le doublage de fréquence à 1,6 µm et la génération paramétrique à 2,1 µm. De plus, la biréfringence artificielle ainsi créée peut être ajustée en modifiant la structure du milieu, ce qui permet de choisir les longueurs d'ondes émises.
Phénomènes limitant l'efficacité d'un OPO
Désaccord de phase
Que se passe-t-il si l'accord de phase n'est pas réalisé, ou s'il est imparfait ? On parle alors de désaccord de phase non nul, et on note dans le cas colinéaire :
Dans ce cas, l'énergie transférée de la pompe au signal et au complémentaire finit par être rendue à la pompe, et ce de manière périodique au cours de la propagation dans le milieu. L'alternance de ces interférences constructives et destructives forme des zones « sombres » et « claires » (du point de vue de l'intensité d'une des trois ondes) qu'on appelle franges de Maker. Pour des puissances de pompe relativement faibles (en dessous de la saturation), l'intensité générée est donnée par :
où g est le gain paramétrique, proportionnel à la non-linéarité du milieu et à l'amplitude de l'onde de pompe, et
 .
.Pour un fort désaccord de phase, la demi période de ces franges est appelée longueur de cohérence et vaut
 . Elle dépend du matériau et des longueurs d'onde utilisés, et peut atteindre des valeurs aussi faibles que 10 μm.
. Elle dépend du matériau et des longueurs d'onde utilisés, et peut atteindre des valeurs aussi faibles que 10 μm.À l'accord de phase parfait en revanche (Δk = 0), la puissance est transférée de façon durable au signal et au complémentaire (en dessous de la saturation), selon la relation :
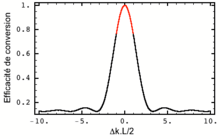
où l'approximation est valable pour un faible gain. Si on s'intéresse à l'intensité en sortie du milieu non-linéaire de longueur L en fonction du désaccord de phase, en se restreignant aux faibles gains, on obtient :
Ce que montre cette formule et la figure ci-contre, c'est que l'intensité générée peut rester importante même avec un faible Δk L : l'accord de phase n'est pas une condition stricte. Autrement dit, le processus de conversion de la pompe vers le signal et le complémentaire restera efficace :
- pour des fréquences de l'onde signal et complémentaire légèrement différentes, à fréquence de pompe fixe : c'est la tolérance en longueur d'onde, ou acceptance spectrale de l'OPO. On parle également de bande passante. Celle-ci est limitée par les différences entre les vitesses de groupe des différentes ondes. Elle est d'autant plus petite que le cristal est long. Sa valeur est très variable et peut atteindre es valeurs aussi importantes que 3 000 GHz (soit plus de 10 nm à 1 μm) ;
- pour des angles de propagation des ondes différents : c'est l'acceptance angulaire de l'OPO. Elle peut être limitante dans le cas de faisceaux fortement focalisés.
Pour la conception d'un OPO, ces tolérances peuvent être des avantages ou des inconvénients, selon ce qu'on souhaite.
Walk-off
L'inconvénient majeur de l'accord de phase par biréfringence est justement... la biréfringence ! En effet, des ondes polarisées différemment vont se propager suivant des directions différentes dans le cristal, en suivant les rayons ordinaire O et extraordinaire E correspondant aux polarisations du même nom. Le décalage des faisceaux diminue leur recouvrement et donc la longueur d'interaction : l'efficacité diminue. Ce phénomène est communément désigné par le terme anglo-saxon de walk-off (littéralement : « marche en dehors »).
Dans certaines situations, il est possible de s'affranchir de cet effet tout en conservant un accord de phase. Dans ce cas les indices vus par les ondes dépendent peu de l'angle de propagation, ce qui rend l'accord de phase très tolérant : on parle alors d'accord de phase non critique.
Accordabilité d'un OPO
Dans un OPO utilisant l'accord de phase par biréfringence, les fréquences des ondes signal et complémentaire peuvent être changées continument par une simple rotation du cristal non-linéaire. En effet, en changeant l'angle θ entre la pompe et le cristal, la condition d'accord de phase sera vérifiée pour des fréquences signal et complémentaire différentes. Comme la conservation de l'énergie reste vérifiée, une augmentation de la fréquence du signal s'accompagnera d'une diminution de la fréquence complémentaire, et vice-versa.
Plus généralement, toute méthode permettant de faire varier sensiblement l'indice extraordinaire par rapport à l'indice ordinaire permet de changer l'accord de phase et donc d'accorder l'OPO. Ainsi, l'accord de phase en température se fait en chauffant un cristal biréfringent.
- tolérance : choix des lambda, accord de phase
- cône de fluorescence paramétrique + photo
- limitations: zone d'accord de phase, deff, transmission
- pas de résonance excitée : accordabilité
- quid de l'accord de phase en température ?
Bistabilité et chaos
Tout comme certaines cavités Fabry-Perot comprenant un milieu non-linéaire, un OPO peut présenter de la bistabilité. Autrement dit, la puissance de sortie à une des longueurs d'onde peut prendre deux valeurs différentes pour une seule valeur de la puissance en entrée. Le passage d'un état à un autre se faisant par un basculement très rapide.
Dans certaines conditions (dépendant des pertes optiques et des longueurs de cavité), la puissance en sortie de l'OPO devient chaotique en fonction de la puissance en entrée. Il est alors possible d'observer les phénomènes de bifurcation par doublement de période et d'attracteur prévus par la théorie du chaos.
Ces phénomènes s'observent préférentiellement dans les OPO triplement résonnants.
Objet quantique ou classique ?
Dans le régime des variables continues (i.e. dans lequel on ne peut plus distinguer individuellement les photons), l'OPO est utilisé pour générer des états non classiques de la lumière. En effet, lorsque l'OPO est pompé sous son seuil d'oscillation, ce dernier présente des propriétés quantiques très intéressantes. On parle d'amplification paramétrique optique non dégénérée dont l'hamiltonien modèle est :

où
 désigne l'opérateur d'annihilation d'un photon de pompe (p), signal (s) et complémentaire (c), et g est une constante de couplage que l'on peut obtenir par une correspondance semi-classique notamment. L'interprétation corpusculaire de la conversion paramétrique est transparente sur cet hamiltonien.
désigne l'opérateur d'annihilation d'un photon de pompe (p), signal (s) et complémentaire (c), et g est une constante de couplage que l'on peut obtenir par une correspondance semi-classique notamment. L'interprétation corpusculaire de la conversion paramétrique est transparente sur cet hamiltonien.Si l'on se place à la dégénérescence de fréquence et de polarisation, et si la pompe est suffisamment intense, l'hamiltonien devient :

où χ désigne une nouvelle constante qui dépend de l'amplitude complexe de la pompe et de la non linéarité du cristal.
Si l'on écrit maintenant l'équation d'évolution des opérateurs d'annihilation, dans la représentation d'interaction, on est conduit à :
![\frac{d}{dt}\widehat{a}(t)=\frac{1}{i\hbar}\left[\widehat{a}(t),\mathcal{H}_{int}\right]=
-\chi\widehat{a}^{\dagger}(t),](3/713e74ecbae73246cb8579966dde7065.png) d'où :
d'où : 
On rappelle l'expression des opérateurs de quadratures :
 La relation d'entrée-sortie de ces opérateurs après un temps d'interaction tint = nL / c dans un cristal non linéaire de longueur L et d'indice n s'écrit :
La relation d'entrée-sortie de ces opérateurs après un temps d'interaction tint = nL / c dans un cristal non linéaire de longueur L et d'indice n s'écrit :
avec r = χtint. On constate donc bien que la quadrature
 est comprimé d'un facteur s = e − 2r alors que la quadrature conjuguée
est comprimé d'un facteur s = e − 2r alors que la quadrature conjuguée  est dilatée d'un facteur 1 / s. La relation d'incertitude qui conditionne les variances de ces quadratures est toujours vérifiée. L'opérateur d'évolution associé à cet hamiltonien d'interaction s'écrit alors de manière générale :
est dilatée d'un facteur 1 / s. La relation d'incertitude qui conditionne les variances de ces quadratures est toujours vérifiée. L'opérateur d'évolution associé à cet hamiltonien d'interaction s'écrit alors de manière générale : que l'on appelle un squeezer.
que l'on appelle un squeezer.Lorsque l'on travaille sous le seuil d'oscillation de l'OPO (i.e. ses pertes ne sont alors plus compensées par l'injection de la pompe), les champs lumineux ont une valeurs moyennes nulles. Le squeezer agit donc sur un état de vide de photons
 . On obtient alors à la sortie de l'OPO des faisceaux toujours vides de photons mais dont les fluctuations sont cette fois comprimées en dessous de la limite quantique standard définies par les fluctuations du vide. Si l'on écrit maintenant cet opérateur complètement en termes des opérateurs
. On obtient alors à la sortie de l'OPO des faisceaux toujours vides de photons mais dont les fluctuations sont cette fois comprimées en dessous de la limite quantique standard définies par les fluctuations du vide. Si l'on écrit maintenant cet opérateur complètement en termes des opérateurs  et
et  , on obtient :
, on obtient :
On constate alors facilement que l'action de cet opérateur sur le vide de photon conduit à un état ne peuplant que les états nombres pairs de photons.
Origine du terme « paramétrique »
En mécanique, un oscillateur paramétrique est un oscillateur dont la fréquence propre est modulée périodiquement, via un paramètre de modulation. Lorsque ce paramètre est modulé à deux fois la fréquence propre, l'amplitude d'oscillation croît exponentiellement. Ainsi, la balançoire est un oscillateur paramétrique puisqu'on balance ses pieds deux fois pendant un aller-retour pour amplifier le mouvement. En optique, le terme a été conservé pour désigner la création d'une onde de basse fréquence (signal) par une onde haute fréquence (pompe). En revanche, il n'est pas nécessaire que la fréquence de la pompe soit égale à deux fois la fréquence du signal. La comparaison s'arrête donc là.
Analogies et différences entre oscillateur paramétrique optique et laser
Les OPO et les lasers ont un certain nombre de points communs :
- ils nécessitent un milieu amplificateur et une cavité optique ;
- ils produisent un rayonnement cohérent et monochromatique de longueur d'onde optique ;
- ils peuvent être pompés par une autre source optique cohérente ;
- leur conception nécessite des connaissances et des technologies proches ou identiques.
En revanche, il existe un certain nombre de différences aussi bien théoriques que pratiques entre ces deux dispositifs, que nous nous proposons de détailler ici.
Trois ondes pour une, deux ou trois résonances
Dans un laser, l'onde générée est également l'onde oscillante. Dans un OPO en revanche, il y a trois ondes optiques couplées entre elles : pompe, signal et complémentaire. On peut alors envisager de nombreux schémas d'OPO selon la façon dont ces ondes sont mises en cavité :
- OPO simplement résonant (SROPO). Le signal est par exemple l'onde oscillante dans la cavité, tandis que le complémentaire générée dans le cristal est libre. On peut alors choisir de n'extraire que le complémentaire, ou bien d'extraire également le signal en employant un miroir de sortie partiellement réfléchissant.
- OPO doublement résonant (DROPO). Signal et complémentaire résonnent tous les deux dans la cavité. Le seuil d'oscillation est plus faible qu'en simplement résonant, ce qui le rend intéressant pour la réalisations d'OPO continus où l'intensité de l'onde pompe est relativement faible. En revanche, il faut que les résonances du signal et du complémentaire coïncident, ce qui n'est généralement pas le cas à cause de la dispersion. De plus, même en cas de coïncidence, la moindre fluctuation de la longueur optique de cavité risque de faire sortir le DROPO de la double résonance. Ce type d'OPO souffre donc d'instabilités de fréquence et d'intensité, particulièrement gênantes en régime continu ou lorsqu'on veut accorder l'OPO en fréquence. Une stabilisation active de la cavité par une électronique d'asservissement peut permettre de maintenir la double résonance. Il existe également des DROPO dans lesquels signal et complémentaire oscillent dans des cavités de longueurs différentes (DROPO à cavités imbriquées), ce qui permet de choisir et contrôler la coïncidence des résonances. Dans tous les cas une conception monolithique et robuste permet d'améliorer les choses.
- PR-DROPO. Un DROPO où l'un des deux ondes résonantes est la pompe.
- OPO triplement résonant (TROPO). Il s'agit d'un DROPO dans lequel la pompe oscille également. Cet OPO souffre des mêmes problèmes que le DROPO, en pire.
- OPO à retour de pompe (PE-OPO). Il s'agit d'un OPO pour lequel la pompe restante après un aller est renvoyée vers l'OPO afin de réaliser un double pompage.
- OPO à amplification intracavité (OPO-OPA). Il s'agit d'un OPO simplement résonant à deux cristaux non-linéaires. L'onde résonante, après passage dans le deuxième cristal, sert de pompe dans le deuxième cristal pour amplifier l'onde non résonante.
- OPO à résonances croisées (CROPO). Il s'agit d'un SROPO à deux cristaux pour lequel le signal est évacué de la cavité après le premier cristal et le complémentaire après le deuxième. La pompe et le signal se mélangent dans le premier cristal pour créer l'onde complémentaire, tandis que ce sont la pompe et le complémentaire qui se mélangent dans le deuxième cristal pour refaire du signal. On peut montrer que cet OPO est réellement simplement résonant car les ondes gardent une relation de phase entre elles qui maintient l'oscillation.
En fait, les variantes sont presque infinies. Il existe par exemple des OPO pour lesquels la pompe à ωp n'est pas issue directement d'un laser externe, mais générée à l'intérieur de la cavité optique par doublage de fréquence dans un cristal non-linéaire pompé à ωp/2 !
Effets thermiques
Une autre différence fondamentale entre un laser et un OPO est le mode de génération de la lumière. L'effet laser nécessite l'absorption de l'énergie de pompe avant restitution à l'onde générée, ce qui entraîne notamment une élévation de température du milieu laser. L'effet paramétrique, comme tous les effets d'optique non-linéaire, ne nécessite pas d'absorption : les électrons du milieu répondent de façon non-linéaire et quasi-instantanée à l'onde de pompe en convertissant celle-ci en ondes de fréquences différentes, mais ne sont pas excités à un niveau d'énergie supérieur. Les effets thermiques sont donc faibles dans un OPO (surtout en régime pulsé), à condition que le cristal utilisé soit très transparent.
Comment démarre un OPO : la fluorescence paramétrique
La fluorescence paramétrique est la lumière générée par la pompe en un passage à travers le milieu non-linéaire. Contrairement à la fluorescence d'un laser qui est incohérente et omnidirectionnelle, la fluorescence paramétrique est une lumière cohérente créée selon une ou plusieurs directions bien particulières dictées par l'accord de phase (voir cône de fluorescence paramétrique). Dans bon nombre d'OPO, cette fluorescence est d'intensité beaucoup trop faible pour être visible à l'œil nu, ou même détectable avec une photodiode.
D'après les équations de l'optique non-linéaire, cette fluorescence ne peut pas être créée à partir de rien : un bruit de départ est nécessaire. Ce bruit est appelé fluorescence paramétrique spontanée par analogie avec les milieux laser. Dans de nombreux travaux scientifiques, ce bruit, à défaut de pouvoir être mesuré, est modélisé par un champ phénoménologique dont l'énergie est celle d'un ou d'un demi photon par mode électromagnétique. On entend ici par mode une solution des équations de Maxwell dans le vide, avec les conditions aux limites imposées par exemple par la cavité optique de l'OPO. L'origine de ce bruit est encore discuté au sein de la communauté scientifique. Il est parfois attribué aux fluctuations quantiques du vide.
Un transfert d'énergie réversible : importance de la phase
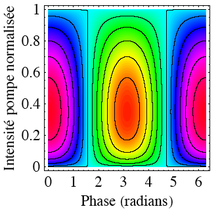
Dans un OPO, les trois ondes pompe, signal, et complémentaires sont fortement couplées et échangent en permanence de l'énergie entre elles. Le sens de ce transfert d'énergie dépend fortement des phases et des intensités relatives de ces ondes. Par exemple, à forte puissance de pompe le signal et le complémentaire peuvent se recombiner pour générer de la pompe, et ainsi de suite. Cet effet de saturation limite la puissance générée et arrive souvent au centre d'un faisceau de pompe gaussien ou au sommet d'une impulsion.
Plus exactement, la génération paramétrique dépend de la phase non-linéaire
 . À chaque endroit z du milieu non-linéaire, l'intensité et les phases de chaque onde dépendent à la fois de l'intensité des deux autres ondes et de la phase non-linéaire ! Les équations non-linéaires gouvernant les amplitudes du champ électrique et les phases s'écrivent :
. À chaque endroit z du milieu non-linéaire, l'intensité et les phases de chaque onde dépendent à la fois de l'intensité des deux autres ondes et de la phase non-linéaire ! Les équations non-linéaires gouvernant les amplitudes du champ électrique et les phases s'écrivent :

Lorsque la phase vaut π/2, les sinus valent 1, et
 est négatif : le transfert d'énergie se fait alors de la pompe vers le signal et le complémentaire. Pour une phase de -π/2, le transfert a lieu dans l'autre sens.
est négatif : le transfert d'énergie se fait alors de la pompe vers le signal et le complémentaire. Pour une phase de -π/2, le transfert a lieu dans l'autre sens.Au démarrage d'un OPO, la phase φ n'est pas déterminée car les ondes signal et complémentaire ne sont que du bruit. Lorsque leur amplitude augmente, leur phase s'ajuste afin que la phase non-linéaire vaille π/2 afin de privilégier le transfert d'énergie de l'onde la plus puissante vers les ondes les plus faibles. Si jamais la pompe tombe à zéro (dépeuplement complet), sa phase n'est plus définie. La phase non-linéaire s'ajuste alors à -π/2 pour maximiser le transfert vers l'onde la plus faible : il y a reconversion vers la pompe.
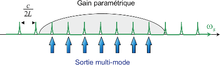
Dans un OPO simplement résonant (SROPO), la phase du signal doit respecter une condition de résonance dans la cavité optique. Elle doit revenir identique à elle-même sur un tour de cavité, soit :
 , où m est un entier relatif, Ls est la longueur optique d'un tour de cavité, et Δφs est le déphasage non-linéaire dû à la conversion paramétrique. Cette condition est réalisée pour un ensemble de modes équidistants en fréquence. Ces modes peuvent osciller s'il respectent la condition d'accord de phase, c'est-à-dire s'ils sont placés dans la courbe de gain de l'OPO, comme résumé sur la figure ci-contre. Comme le complémentaire n'est pas contraint par la cavité, sa phase s'ajuste automatiquement pour stabiliser la phase non-linéaire à π/2, là où le transfert d'énergie est le plus efficace, et donc là où le seuil de l'OPO est le plus bas. Ainsi il est toujours possible d'obtenir l'oscillation du signal avec un transfert de la pompe vers les deux autres ondes.
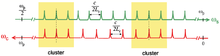
, où m est un entier relatif, Ls est la longueur optique d'un tour de cavité, et Δφs est le déphasage non-linéaire dû à la conversion paramétrique. Cette condition est réalisée pour un ensemble de modes équidistants en fréquence. Ces modes peuvent osciller s'il respectent la condition d'accord de phase, c'est-à-dire s'ils sont placés dans la courbe de gain de l'OPO, comme résumé sur la figure ci-contre. Comme le complémentaire n'est pas contraint par la cavité, sa phase s'ajuste automatiquement pour stabiliser la phase non-linéaire à π/2, là où le transfert d'énergie est le plus efficace, et donc là où le seuil de l'OPO est le plus bas. Ainsi il est toujours possible d'obtenir l'oscillation du signal avec un transfert de la pompe vers les deux autres ondes.Dans un OPO doublement résonant (DROPO), les choses se compliquent puisque signal et complémentaires doivent tous deux osciller dans la cavité. Il y a donc deux conditions de phase à respecter :


Cette double condition doit également être compatible avec l'accord phase et la conservation de l'énergie. Un DROPO est donc un système surcontraint, ce qui rend l'oscillation possible que pour un nombre restreint de fréquences signal et complémentaire, appelées coïncidences. Ces coïncidences peuvent être partielles, ce qui donne lieu à des « paquets » de modes voisins oscillants, appelés clusters. Lorsque la longueur de la cavité fluctue légèrement (5 nm peuvent suffire), les peignes de fréquence signal et complémentaire se dilatent, et les coïncidences se retrouvent sur d'autres paires de modes. Ces sauts de modes peuvent se produire entre modes voisins ou d'un cluster à l'autre, ce qui entraîne de fortes instabilités de fréquence et d'intensité, en particulier lorsqu'il s'agit d'accorder l'OPO.
[conséquences sur la phase..]
Dans un DROPO en cavité linéaire, le signal et le complémentaire font un aller-retour dans le milieu non-linéaire pendant un tour de cavité. Au retour, l'accord de phase avec la pompe n'est pas possible puisqu'elle se propage dans la direction opposée. En l'absence de pompe, signal et complémentaire vont se combiner pour refaire de la pompe, selon le processus expliqué plus haut. Cette reconversion peut atteindre des valeurs aussi élevées que 20 % de l'énergie de pompe initiale.
Dans un SROPO ou une cavité en anneau (où les ondes ne circulent que dans un sens), les phénomènes de reconversion au retour n'existent pas, sauf en cas de réflexions parasites sur les optiques de la cavité (miroirs, faces du cristal...).
Qualité spatiale des faisceaux
Dans un laser, la qualité spatiale du laser est principalement déterminée par la cavité optique (et les effets thermiques dans le milieu laser) et non par la qualité du faisceau de pompe. En effet, l'énergie de la pompe est d'abord absorbée dans le milieu actif avant d'être restituée au faisceau laser par émission stimulée. Un laser peut donc être utilisé pour faire de la transformation de mode, c'est-à-dire générer un faisceau lumineux de bonne qualité spatiale à partir d'un faisceau de pompe de qualité moyenne.
Dans un OPO en revanche, les inhomogénéités spatiales du faisceaux de pompe sont fortement transmises aux ondes signal et complémentaire (avant d'être partiellement filtrées par diffraction dans la cavité). En effet, dans le milieu non-linéaire les trois ondes s'échangent de l'énergie de façon locale et quasi-instantanée. De plus, comme la conversion non-linéaire est d'autant plus importante que l'intensité est grande, les « points chauds » de la pompe auront tendance à être amplifiés. Cet effet est particulièrement important dans les OPO en régime impulsionnel, où les faisceaux sont peu filtrés par la cavité optique en raison du faible nombre d'aller-retours.
Effets thermiques dans un OPO
Comme l'énergie des ondes n'est pas stockée dans le milieu non-linéaire, les effets thermiques dans un OPO sont beaucoup plus faibles que dans un laser. Cependant, même les cristaux non-linéaires les plus purs possèdent une absorption résiduelle. De plus, la zone de transparence des cristaux est limitée en longueur d'onde. Ainsi, l'absorption du complémentaire au delà de 4 μm est une limitation bien connue des OPO à base de cristaux d'oxydes ferroélectriques tels que le niobate de lithium. Dans les OPO continus pour lesquels le seuil d'oscillation est élevé l'absorption résiduelle de la pompe devient non négligeable. Dans les OPO impulsionnels à fort taux de répétition (typiquement > kHz), la puissance moyenne absorbée peut devenir assez élevée pour créer une lentille thermique qui modifie la stabilité de la cavité. Les conséquences peuvent être : un profil spatial des faisceaux dégradé ou une instabilité en puissance (avec éventuellement une hystérésis en fonction de la puissance de pompe).
Exemples d'OPO
OPO continu à base de PPLN
Les OPO continus sont souvent constitués d'une cavité stable à miroirs concaves. Le seuil d'oscillation étant plus haut qu'en impulsionnel, le faisceau de pompe doit être focalisé assez petit (typiquement sur un diamètre de 100 μm). Pour des raisons d'efficacité, les modes propres de la cavité pour la ou les ondes résonnantes doivent être de diamètre comparable. Cela impose des rayons de courbure des miroirs assez petits (typiquement 100 mm) et des longueurs de cavité assez longues (typiquement 1 m). Pour réduire son encombrement la cavité est souvent repliée en "papillon", en "L" ou en "Z". Pour abaisser le seuil d'oscillation à des valeurs atteignables avec des lasers de pompe existant, il est préférable de choisir un cristal fortement non-linéaire, tel que le niobate de lithium périodiquement retourné (PPLN), et parfois de rendre l'OPO doublement résonnant.
OPO impulsionnel à base de KTP
Le Phosphate de potassium titanyl, KTiOPO4 (KTP), est un cristal transparent dans la gamme 350-4500 nm. Il est souvent utilisé pour produire du rayonnement infrarouge à 4 µm à partir d'un laser Nd:YAG à 1,064 µm déclenché activement. La configuration de base de ce type d'OPO est une cavité optique dite instable constituée de deux miroirs plans, et d'un cristal de section relativement grande (~ 1 cm) afin de pouvoir utiliser des faisceaux de grande dimension et donc très énergétiques. Le faisceau de pompe peut être amené soit à travers un des miroirs, soit par un miroir intracavité à 45°; elle est alors éjectée grâce à un deuxième miroir à 45° situé après le cristal. La compensation (partielle) du walk-off se fait traditionnellement par l'emploi de deux cristaux de KTP avec une orientation particulière des axes optiques. Ce type de source est accordable en longueur d'onde par une simple rotation du ou des cristaux.
OPO PPKTP à différence de fréquence intracavité
- quelques cristaux : Potassium Titanyl Phosphate, KTiOPO4 (KTP) (doubleur de fréquence)
- quelques dispos ?
- autres milieux non-linéaires : liquides, gaz, fibres, etc.
Bibliographie
- Nicolas Forget, Des amplificateurs laser aux amplificateurs paramétriques, Thèse de doctorat de l'École Polytechnique, soutenue le 5 octobre 2005. Résumé sur le site web de l'ONERA
- Jean-François Roch, Introduction à l'optique non-linéaire, cours de 3e année de l'École supérieure d'optique (SupOptique) (2004)
- Paul Mandel, Introduction à l'optique non-linéaire, Université Libre de Bruxelles, PHYS 327, (2003). Cours téléchargeable en ligne, soumis à un copyright.
- M. M. Fejer & al., Quasi-Phase-Matched Second Harmonic Generation : Tuning and Tolerances, IEEE J. of Quantum Electron. 28 (11), 2631-2654 (1992)
- G. Leo & al., Parametric fluorescence in oxidized AlGaAs waveguides, J. Opt. Soc. Am. B 16 (9), 1597-1602 (1999)
- A. Fiore & al., Second harmonic generation at λ=1.6 µm in AlGaAs/Al2O3 waveguides using birefringence phase matching, Appl. Phys. Lett. 72, 2942-2944 (1998)
- M. Ebrahimzadeh, Infrared Optical Parametric Oscillators : Current and Future Perspectives, exposé donné aux Journées Scientifiques de l'ONERA le 5 février 2007. Fichier PDF de la présentation
- R. L. Byer & al., Power and bandwidth of spontaneous parametric emission, Phys. Rev. 168, 1064-1068 (1968)
- T. G. Giallorenzi & al., Quantum theory of spontaneous parametric scattering of intense light, Phys. Rev. 166, 225-233 (1968)
- D. A. Kleinman & al., Theory of optical parametric noise, Phys. Rev. 174, 1027-1041 (1968)
Liens externes
- Manuel Joffre, Optique non-linéaire, cours de DEA de physique quantique de l'École polytechnique.
- Rick Trebino, notes de cours de physique moderne, dont quelques chapitres sur l'optique non-linéaire (en anglais).
Wikimedia Foundation. 2010.












![I_{s,c}\left(z\right)=I_{s,c}\left(0\right)\left[1+\frac{g^2}{K^2}\sin^2\left(K z\right)\right]\,](5/5e52bc4124b8a2d8915783f203d9f197.png)
![I_{s,c}\left(z\right)=I_{s,c}\left(0\right)\cosh^2\left(g z\right)\approx I_{s,c}\left(0\right)\left[1+\frac{1}{2}\left(g z\right)^2\right]\,](4/604dc4516dc4eae3e068d364e8e2776b.png)
![I_{s,c}\left( \frac{\Delta k L}{2}\right)=I_{s,c}\left(0\right)\left[1+\left(g L\right)^2 \operatorname{sinc}^2\left(\frac{\Delta k L}{2}\right)\right]\,](7/7477ea59c5b3658f5611d608f65e655a.png)