Orbite midi-minuit

Étymologiquement et par analogie avec l'orbite géosynchrone, une orbite héliosynchrone (du grec ancien Ἥλιος, èlios, personnification du soleil) est une orbite héliocentrique de rayon ~24,360 Gm (0,1628 ua) telle que la période de révolution de l'objet coïncide avec la période de rotation du Soleil. L'orbite héliostationnaire est l'orbite héliosynchrone d'inclinaison et d'excentricité orbitale zéro.

Sommaire 1 Principe 2 Techniques 3 Éléments techniques 4 Historique 5 Voir aussi 6 Référence

Principe

Mais l'usage le plus répandu de l'expression orbite héliosynchrone concerne surtout une orbite géocentrique dont on choisit l'altitude et l'inclinaison de façon à ce que l'angle entre le plan d'orbite et la direction du soleil demeure à peu près constant, en dépit de la dérive du nœud ascendant de l'orbite qui se traduit par la précession du plan de cette orbite. Cette dérive est due à l'influence du bourrelet équatorial de la Terre. Elle dépend de l'inclinaison, du grand axe et de l'excentricité de l'orbite. Un satellite placé sur une telle orbite repasse au-dessus d'un point donné de la surface terrestre à la même heure solaire locale. Ceci est souhaitable lorsqu'on prend des photographies de ce point en lumière visible, car l'éclairement solaire sera peu variable d'un cliché à l'autre (satellites météorologiques, espions, de télédétection, etc.). Il y aura une oscillation annuelle de l'heure solaire du passage à cause de l'excentricité orbitale terrestre (voir analemme).

Techniques

Ces orbites sont possibles pour une gamme d'altitudes autour typiquement de 600–1000 km, pour des périodes de 96–110 min, avec une inclinaison, qui lui est liée, d'environ 98 à 100°. La dérive du plan de l'orbite est alors de 0,9856 degré par jour, soit 360° par an.

Des options sont possibles autour de ce schéma de base: un satellite pourrait avoir une orbite héliosynchrone fortement excentrique, auquel cas l'« heure solaire fixe de passage » n'est pertinente que pour un point donné de l'orbite, typiquement le périgée. Mais dans ce cas interviendrait une autre influence du bourrelet équatorial, la rotation du périgée dans le plan de l'orbite (cf. Orbite de Molniya); cela ôte beaucoup d'intérêt à une orbite elliptique. Les orbites héliosynchrones sont quasiment toutes circulaires.

La période orbitale choisie, donc l'altitude, dépend, elle, du taux de passage quotidien désiré; le satellite traverse le plan équatorial à la même heure solaire à chaque passage, mais à une longitude différente lors de chaque passage car la Terre tourne sous lui. Par exemple, une période orbitale de 96 min, qui se divise entièrement dans un jour solaire (15 fois), signifiera que le satellite traversera l'équateur à quinze longitudes différentes lors d'orbites consécutives, pour revenir à la première longitude à chaque quinzième passage, une fois par jour.

L'orbite midi/minuit est un cas particulier de l'orbite héliosynchrone où l'heure solaire fixe de passage est aux environs de midi ou minuit pour les longitudes équatoriales. L'orbite crépusculaire, d'une manière similaire, est une orbite héliosynchrone dont l'heure solaire fixe de passage coïncide avec le lever ou le coucher du Soleil.

Au fur et à mesure que l'altitude du satellite augmente, l'inclinaison requise augmente aussi, si bien que l'utilité de l'orbite diminue doublement. Premièrement parce que la définition des clichés diminue lorsque la distance de prise de vues augmente, et deuxièmement parce que l'inclinaison croissante, (supérieure à 90 degré pour une orbite rétrograde), implique que le satellite ne survolera plus les hautes latitudes. Les orbites héliosynchrones typiques sont inclinées à 98°, ce qui assure une bonne couverture du globe terrestre.

L'orbite héliosynchrone est également possible autour de certaines autres planètes, comme Mars, dont l'aplatissement est le double de celui de la Terre. La sonde Mars Global Surveyor survole ainsi Mars à 14 heures sur une orbite quasi-phasée de 88 orbites en 7 sols (elle se décale de 59 kilomètres à l'est à chaque cycle).

Éléments techniques

Pour une orbite directe, la précession est rétrograde, c'est-à-dire, en sens opposé à celui de la rotation terrestre ; aussi les orbites héliosynchrones sont-elles rétrogrades, assurant une précession directe. Une bonne approximation du taux de précession pour le cas particulier d'une orbite circulaire (excentricité nulle) est donnée par :

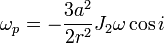
Où ω_p est le taux de précession du nœud ascendant en (rad/s), a est le rayon équatorial terrestre (6,378 137 Mm), r est le rayon orbital du satellite, ω sa fréquence angulaire (2π radians divisé par sa période), i son inclinaison et J₂ est le second facteur de forme dynamique terrestre (1,08×10^-3). Cette dernière quantité est liée à l'aplatissement comme suit :

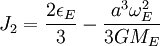
Où ε_E est l'aplatissement terrestre, ω_E le taux de rotation terrestre (7,292 115×10^-5 rad/s), et GM_E est le produit de la constante gravitationnelle universelle et de la masse terrestre (3,986 004 418×10¹⁴ m³/s²).

Une formule simple, déduite de la formule ci-dessus, relie les quantités r, a et i :

r / a = 1,93669 (- cos i) ^2/7

Historique

Samos-2 fut le premier satellite artificiel à atteindre une orbite héliosynchrone en 1961.

Voir aussi

• Orbite

Référence

• Cours de mécanique spatiale
• Sandwell, David T., The Gravity Field of the Earth - Part 1 (2002) (p. 8)
• (en) [pdf] Ronald J. Boain, « A-B-Cs of Sun-Synchronous Orbit Mission Design », 2004, Jet Propulsion Laboratory

• Portail de l’astronautique
• Portail de l’astronomie