Nullstellensatz

Nullstellensatz

Théorème des zéros de Hilbert

Le théorème des zéros de Hilbert, parfois appelé Nullstellensatz, est un théorème central de géométrie algébrique qui fait le lien entre les idéaux et les variétés algébriques. Il a été démontré par le mathématicien allemand David Hilbert.

Énoncé

Il existe plusieurs formulations équivalentes du théorème des zéros de Hilbert.

Théorème 1

Soit K un corps, L une K-algèbre de type fini.

Si L est un corps, alors L est une extension algébrique finie de K.

Thèorème 2 (Nullstellensatz)

Si K est algébriquement clos, on a :

Si M est un idéal maximal de l'anneau des polynômes en n indéterminées, noté K[X1,...,Xn], il existe un n-uplet (a k) de Kn tel que l'idéal M soit engendré par la famille (X k - a k).


Démonstration

Soit M un idéal maximal de K[X_1,\ldots ,X_n]\,.

L:= K[X_1,\ldots ,X_n] /\ M est une K-algèbre de type fini, et L est un corps puisque M est maximal.

D'après le théorème 1, L est un extension algébrique de K qui est lui même algébriquement clos.

On a donc K=L.

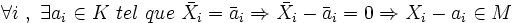Donc \forall i \ ,\ \exists a_i \in K \ tel\ que\ \bar X_i = \bar a_i \Rightarrow \bar X_i - \bar a_i =0 \Rightarrow X_i-a_i \in M.

On a donc 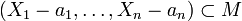(X_1-a_1,\ldots ,X_n-a_n) \subset M, mais comme M est maximal, on a l'égalité.

Théorème 3 (Existence des zéros)

Si K est un corps algébriquement clos, alors pour tout idéal propre I de K[X1,...,Xn], il existe un point de Kn racine de tout élément de I.

Ce résultat n'est pas vrai si K n'est pas algébriquement clos. L'idéal M des multiples de X2 + 1 est maximal dans R[X] puisque le quotient de R[X] par M est un corps isomorphe à C, pourtant le polynôme n'admet pas de racine dans r.


Démonstration

Soit K un corps algébriquement clos. Soit I un tel idéal.

I est inclus dans un idéal maximal M, d'où d'après le théorème 2, 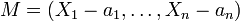M=(X_1-a_1,\ldots ,X_n-a_n)\, et donc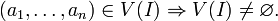 (a_1,\ldots ,a_n)\in V(I)\Rightarrow V(I) \ne \varnothing.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me des z%C3%A9ros de Hilbert ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nullstellensatz de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Nullstellensatz — Der Name Nullstellensatz wird in der Mathematik in unterschiedlichen Zusammenhängen benutzt: für den auch in der englischsprachigen Literatur als Nullstellensatz bekannten hilbertschen Nullstellensatz für einen Spezialfall des Zwischenwertsatzes… …   Deutsch Wikipedia

  • Hilbert's Nullstellensatz — (German: theorem of zeros, or more literally, zero locus theorem – see Satz) is a theorem which establishes a fundamental relationship between geometry and algebra. This relationship is the basis of algebraic geometry, an important branch of… …   Wikipedia

  • Hilbertscher Nullstellensatz — Der hilbertsche Nullstellensatz stellt in der Mathematik in der klassischen algebraischen Geometrie die zentrale Verbindung zwischen Idealen und affinen algebraischen Varietäten her. Er wurde von David Hilbert bewiesen. Es gibt verschiedene… …   Deutsch Wikipedia

  • Hilberts Nullstellensatz — Der Hilbertsche Nullstellensatz stellt in der Mathematik in der klassischen algebraischen Geometrie die zentrale Verbindung zwischen Idealen und affinen algebraischen Varietäten her. Er wurde von David Hilbert bewiesen. Es gibt verschiedene… …   Deutsch Wikipedia

  • Hilbert Nullstellensatz — El Hilbert Nullstellensatz (en alemán: teorema de los ceros ) es un teorema en Geometría algebraica que relaciona variedades e ideales en anillos de polinomios sobre cuerpos algebraicamente cerrados. Fue probado inicialmente por David Hilbert.… …   Enciclopedia Universal

  • Polynomial ring — In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the …   Wikipedia

  • Restricted sumset — In additive number theory and combinatorics, a restricted sumset has the form where are finite nonempty subsets of a field F and is a polynomial over F. When …   Wikipedia

  • Differentially closed field — In mathematics, a differential field K is differentially closed if every finite system of differential equations with a solution in some differential field extending K already has a solution in K. This concept was introduced by Robinson (1959).… …   Wikipedia

  • Théorème des zéros de Hilbert — Le théorème des zéros de Hilbert, parfois appelé Nullstellensatz, est un théorème d algèbre commutative qui est à la base du lien entre les idéaux et les variétés algébriques. Il a été démontré par le mathématicien allemand David Hilbert.… …   Wikipédia en Français

  • Rabinowitsch trick — In mathematics, the Rabinowitsch trick, introduced by harvtxt|Rabinowitsch|1929is a short way of proving the general case of the Hilbert Nullstellensatz from an easier special case, by introducing an extra variable. The Rabinowitsch trick goes as …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”