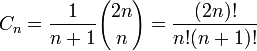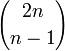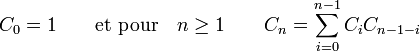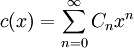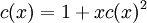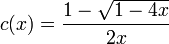Nombres de Catalan

Nombres de Catalan

Nombres de Catalan

Les nombres de Catalan sont des entiers naturels qui se rencontrent souvent dans les problèmes de combinatoire. Ils forment une suite dont le terme d'indice n, appelé nème nombre de Catalan est défini par

C_n = \frac{1}{n+1}{2n \choose n} = \frac{(2n)!}{n! (n+1)!}

(voir coefficient binomial). Les premiers nombres de Catalan (suite A000108 de l’OEIS) pour n=0, 1, 2, 3, ... sont

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862,...

Tous les nombres de Catalan sont des entiers naturels parce qu'ils peuvent s'écrire sous la forme:

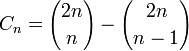
pour n≥1, C_n={2n \choose n}-{2n \choose n-1}

Sommaire

Applications en combinatoire

Mots de Dyck

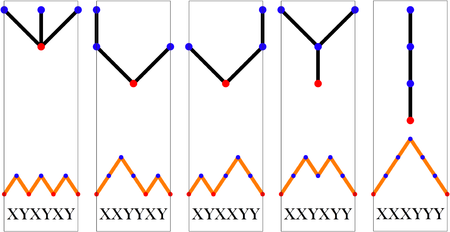
Cn est égal au nombre de mots de Dyck de longueur 2n. Un mot de Dyck est un mot formé de n lettres X et de n lettres Y, tel qu'aucun préfixe (mot obtenu en supprimant les dernières lettres à partir d'un rang quelconque) ne contienne plus de Y que de X. Autrement dit, lorsque nous parcourons un mot de Dyck de gauche à droite, le nombre de X rencontrés est toujours supérieur ou égal au nombre de Y. Par exemple, les mots de Dyck de la longueur 6 sont:

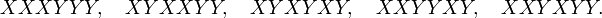
XXXYYY,\quad XYXXYY,\quad XYXYXY,\quad XXYYXY,\quad XXYXYY.

En l'occurrence, C3= 5.

Assimilant X à une parenthèse ouvrante et Y à une parenthèse fermante, un mot de Dyck de longueur 2n peut être vu comme une expression formée de n paires de parenthèses correctement assemblées: ((())), ()(()), ()()(), (())(), (()()). Les mots de Dyck peuvent être naturellement représentés comme des chemins dans un quadrillage de n+1 points par n+1 points, reliant certains points par les traits verticaux et horizontaux. Ces chemins commencent dans le coin inférieur gauche, et se terminent dans le coin supérieur droit, en allant toujours vers le haut ou vers la droite, mais ne passant jamais au-dessus de la diagonale principale. X représente alors un « déplacement vers la droite » et Y représente un « déplacement vers le haut ».
Nous pouvons compter les mots de Dyck avec l'astuce suivante due à D. André (principe de symétrie): intéressons nous aux mots contenant n X et n Y qui ne sont pas des mots de Dyck. Dans de tels mots, déterminons le premier Y qui brise la condition de Dyck, puis modifions toutes les lettres qui suivent ce Y, en échangeant X avec Y et vice versa. Nous obtenons un mot avec n+1 Y et n-1 X, et en fait tous les mots comportant n+1 Y et n-1 X peuvent être obtenus par ce moyen et de manière unique. Le nombre de ces mots est le nombre de façons de placer les n-1 X dans 2n emplacements et est égal à

{2n \choose n-1}

ce qui donne le nombre de mots qui ne sont pas de Dyck; le nombre de mots de Dyck s'en déduit et est égal à

{2n \choose n}-{2n \choose n-1}

qui est le n-ème nombre de Catalan Cn.

Parenthèsages

Cn est également le nombre de façons différentes de placer des parenthèses autour de n+l facteurs. Pour n = 3 par exemple, nous obtenons 5 façons différentes de placer des parenthèses autour de 4 facteurs: a(b(cd)), a((bc)d), (ab)(cd), (a(bc))d, ((ab)c)d. De telles expressions peuvent être naturellement représentées par des arbres binaires complets ordonnés, et Cn donne également le nombre de ces arbres à n+1 feuilles.

Triangulations d'un polygone

Cn est également égal au nombre de différentes façons dont un polygone à n+2 côtés peut être partagé en triangles en reliant ses sommets par des segments de droite.

Catalan number polygons example.png

Partitions non croisées

Cn est également le nombre de partitions non croisées de l'ensemble {1, ..., n }. A fortiori, Cn n'excède jamais le nème nombre de Bell.

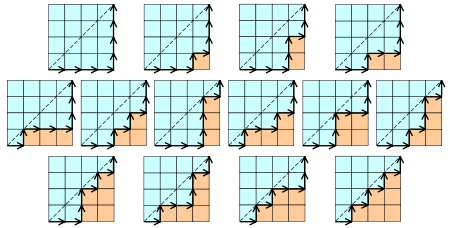
Chemins sous-diagonaux dans le carré

Cn est le nombre de chemins monotones le long des arêtes d'une grille à n × n carrés, qui restent sous (ou au niveau de) la diagonale. Un chemin monotone part du coin Sud-Ouest, arrive dans le coin Nord-Est, et est constitué d'arêtes dirigées à droite ou vers le haut. Un mot de Dyck encode un tel chemin de la manière suivante : X signifie « va à droite ! et Y signifie « monte ! ». Les diagrammes ci-dessous représentent le cas n = 4 :

Catalan number 4x4 grid example.svg

Trajectoires de la marche aléatoire simple

Bijection entre chemins et arbres planaires

Cn est le nombre de trajectoires de longueur 2n+1 d'une marche aléatoire simple qui ont la propriété d'aller de la hauteur 0 à la hauteur 1 en restant négatif ou nul lors des 2n premières étapes. On peut voir cela en faisant pivoter de 45 degrés le chemin entre les deux coins d'un carré décrit lors du premier exemple. C'est aussi le nombre de trajectoires de longueur 2n+2 allant de la hauteur 0 à la hauteur 0 en restant strictement positives lors des 2n+1 étapes intermédiaires, ou encore le nombre de trajectoires de longueur 2n allant de la hauteur 0 à la hauteur 0 en restant positives ou nulles lors des 2n-1 étapes intermédiaires. Dans ce dernier cas on peut coder la trajectoire par une suite de 2n + et de - (pour montée et descente), la condition de positivité se traduisant par le fait que cette suite est un mot de Dyck (car chaque préfixe a plus de montées que de descentes). Ainsi, pour la marche aléatoire simple, la probabilité que le premier temps de retour en 0, partant de 0, ait lieu à l'instant 2n+2, est 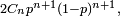\scriptstyle 2C_n p^{n+1}(1-p)^{n+1},\ le facteur 2 prenant en compte les trajectoires strictement négatives en plus des trajectoires strictement positives. De même, la probabilité que le premier temps d'atteinte de 1, partant de 0, ait lieu à l'instant 2n+1, est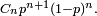 \scriptstyle C_n p^{n+1}(1-p)^{n}.\

Arbres planaires

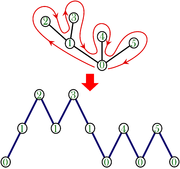
Cn est le nombre d'arbres planaires enracinés à n arêtes. La bijection avec les mots de Dyck, ou encore avec les trajectoires de marches aléatoires, est donnée très visuellement par un parcours extérieur de l'arbre. La trajectoire obtenue est le graphe de la fonction qui à chaque coin (secteur angulaire délimité par un sommet et deux arêtes contigües issues de ce sommet) associe la hauteur du sommet (la distance du sommet à la racine). Les coins sont parcourus dans l'ordre correspondant au parcours autour de l'arbre (voir figure ci-contre). Chaque sommet est visité autant de fois qu'il y a de coins issus de ce sommet, i.e. le nombre de visites à un sommet est le degré de ce sommet ; à titre d'exception, le nombre de visites à la racine est son degré plus un (plus le retour final à la racine, qui revient à visiter 2 fois le coin origine). Ainsi le nombre de pas de la marche est la somme des degrés du graphe, i.e. deux fois le nombre d'arêtes du graphe.

Bijection entre les 5 arbres à 3 arêtes (ligne supérieure), les 5 trajectoires positives de longueur 6 (ligne intermédiaire) et les mots de Dyck correspondants (ligne inférieure).

Relation de récurrence et comportement asymptotique

Les nombres de Catalan satisfont la relation de récurrence

C_0 = 1 \qquad \mbox{et pour}\quad n\ge 1 \qquad C_n=\sum_{i=0}^{n-1}C_i C_{n-1-i}

Ceci vient du fait que tout mot de Dyck w de longueur supérieure à 2 peut s'écrire de manière unique sous la forme

w = Xw1Yw2,

où w1 et w2 désignent des mots de Dyck (éventuellement vides). La fonction génératrice des nombres de Catalan est définie par

c(x)=\sum_{n=0}^\infty C_n x^n

et en utilisant la relation de récurrence ci-dessus nous voyons que

c(x)=1+xc(x)^2\,

et par conséquent

c(x) = \frac{1-\sqrt{1-4x}}{2x}

Asymptotiquement, les nombres de Catalan se comportent comme

C_n \sim \frac{4^n}{n^{3/2}\sqrt{\pi}}

Histoire

La suite de Catalan fut décrite pour la première fois au XVIIIe siècle par Leonhard Euler, qui s'était intéressé au nombre de différentes façons de partager un polygone en triangles. La première publication sur ces nombres est due à Segner et la suite porte alors le nom de Nombre de Segner. Eugène Charles Catalan fit le lien avec le nombre d'expressions « parenthésées » et le nom de Catalan remplaça celui de Segner. L'astuce de comptage des mots de Dyck fut trouvée par Désiré André en 1887.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nombres de Catalan ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombres de Catalan de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Nombres de Segner — Nombres de Catalan Les nombres de Catalan sont des entiers naturels qui se rencontrent souvent dans les problèmes de combinatoire. Ils forment une suite dont le terme d indice n, appelé nème nombre de Catalan est défini par (voir coefficient… …   Wikipédia en Français

  • Catalan (Homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le catalan, une langue parlée essentiellement en Catalogne, pays ayant pour capitale Barcelone et intégrant l État espagnol ; les pays catalans, un… …   Wikipédia en Français

  • Catalan (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le catalan, une langue parlée essentiellement en Catalogne, pays ayant pour capitale Barcelone et intégrant l État espagnol ; les pays catalans, un… …   Wikipédia en Français

  • Nombres 10 000 a 99 999 — Nombres 10 000 à 99 999 Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de dix mille (10 000) à quatre vingt dix neuf mille neuf cent quatre vingt dix neuf (99 999). Article détaillé : 10 000 (nombre).… …   Wikipédia en Français

  • Nombres 10 000 À 99 999 — Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de dix mille (10 000) à quatre vingt dix neuf mille neuf cent quatre vingt dix neuf (99 999). Article détaillé : 10 000 (nombre). Sommaire 1 Nombres dans l …   Wikipédia en Français

  • Nombres 100 000 000 a 999 999 999 — Nombres 100 000 000 à 999 999 999 Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de cent millions (100 000 000) à neuf cent quatre vingt dix neuf millions neuf cent quatre vingt dix neuf mille neuf cent… …   Wikipédia en Français

  • Nombres 100 000 000 À 999 999 999 — Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de cent millions (100 000 000) à neuf cent quatre vingt dix neuf millions neuf cent quatre vingt dix neuf mille neuf cent quatre vingt dix neuf (999 999 999).… …   Wikipédia en Français

  • Nombres 100 000 a 999 999 — Nombres 100 000 à 999 999 Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de cent mille (100 000) à neuf cent quatre vingt dix neuf mille neuf cent quatre vingt dix neuf (999 999). Article… …   Wikipédia en Français

  • Nombres 100 000 À 999 999 — Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de cent mille (100 000) à neuf cent quatre vingt dix neuf mille neuf cent quatre vingt dix neuf (999 999). Article détaillé : 100 000 (nombre).… …   Wikipédia en Français

  • Nombres 1 000 000 a 9 999 999 — Nombres 1 000 000 à 9 999 999 Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de un million (1 000 000) à neuf millions neuf cent quatre vingt dix neuf mille neuf cent quatre vingt dix neuf… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”