Nombre sphenique

Nombre sphenique

Nombre sphénique

Un nombre sphénique est un entier strictement positif qui est le produit de trois facteurs premiers distincts.

La définition exige que chacun des trois facteurs premiers ne soit exprimé qu'une seule fois ; par exemple 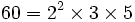60 = 2^2 \times 3 \times 5\, possède bien 3 facteurs premiers, mais n'est pas sphénique car le facteur 2 y est deux fois.

Tous les nombres sphéniques ont exactement huit diviseurs. Si nous exprimons un nombre sphénique sous la forme n = p \times q \times r, où p, q et r sont des nombres premiers distincts, alors l'ensemble de ses diviseurs est :

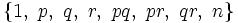\left\{ 1, \ p, \ q, \ r, \ p q, \ p r, \ q r, \ n \right\}.

Par définition, tous les nombres sphéniques sont des entiers sans facteur carré. L'image d'un nombre sphénique par la fonction de Möbius vaut -1.

Les quelques premiers nombres sphéniques sont : 30, 42, 66, 70, 78, 102, 105, 110, 114, 130, 138, 154, 165, 170, 174, 182, 186, 190, ..., 230, 231, ...[1]

On aura :

  • 30 = 2 x 3 x 5
  • 42 = 2 x 3 x 7
  • 66 = 2 x 3 x 11
  • 70 = 2 x 5 x 7
  • 78 = 2 x 3 x 13
  • ...

Les deux premiers nombres sphéniques consécutifs sont 230 = 2×5×23 et 231 = 3×7×11.

Les trois premiers sont 1309 = 7×11×17, 1310 = 2×5×131, et 1311 = 3×19×23.

Il est impossible d'avoir quatre nombres sphéniques consécutifs, puisque sur quatre entiers strictement positifs consécutifs, il y en a un divisible par 4 = 2 x 2 : cet entier ne sera donc pas sans facteur carré.

Références

  • (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Sphenic number ».

Liens externes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nombre sph%C3%A9nique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre sphenique de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Nombre Sphénique — Un nombre sphénique est un entier strictement positif qui est le produit de trois facteurs premiers distincts. La définition exige que chacun des trois facteurs premiers ne soit exprimé qu une seule fois ; par exemple possède bien 3 facteurs …   Wikipédia en Français

  • Nombre sphénique — Un nombre sphénique est un entier strictement positif qui est le produit de trois facteurs premiers distincts. La définition exige que chacun des trois facteurs premiers ne soit exprimé qu une seule fois ; par exemple possède bien 3 facteurs …   Wikipédia en Français

  • Nombre Composé — Un nombre composé est un nombre entier positif qui possède un diviseur positif autre que un ou lui même. Par définition, chaque entier plus grand que un est soit un nombre premier, soit un nombre composé. Les nombres zéro et un ne sont considérés …   Wikipédia en Français

  • Nombre compose — Nombre composé Un nombre composé est un nombre entier positif qui possède un diviseur positif autre que un ou lui même. Par définition, chaque entier plus grand que un est soit un nombre premier, soit un nombre composé. Les nombres zéro et un ne… …   Wikipédia en Français

  • Nombre composé — Un nombre composé est un entier naturel différent de 0 qui possède un diviseur positif autre que 1 ou lui même. Par définition, chaque entier plus grand que 1 est donc soit un nombre premier, soit un nombre composé, et les nombres 0 et 1 ne sont… …   Wikipédia en Français

  • 400 (nombre) — Nombres 400 à 499 Cet article recense les nombres qui ont des propriétés remarquables allant de quatre cents (400) à quatre cent quatre vingt dix neuf (499). Sommaire 1 Entiers de 400 à 409 2 Entiers de 410 à 419 3 Entiers de 420 à 429 …   Wikipédia en Français

  • 400 à 499 (nombre) — Nombres 400 à 499 Cet article recense les nombres qui ont des propriétés remarquables allant de quatre cents (400) à quatre cent quatre vingt dix neuf (499). Sommaire 1 Entiers de 400 à 409 2 Entiers de 410 à 419 3 Entiers de 420 à 429 …   Wikipédia en Français

  • 401 (nombre) — Nombres 400 à 499 Cet article recense les nombres qui ont des propriétés remarquables allant de quatre cents (400) à quatre cent quatre vingt dix neuf (499). Sommaire 1 Entiers de 400 à 409 2 Entiers de 410 à 419 3 Entiers de 420 à 429 …   Wikipédia en Français

  • 450 (nombre) — Nombres 400 à 499 Cet article recense les nombres qui ont des propriétés remarquables allant de quatre cents (400) à quatre cent quatre vingt dix neuf (499). Sommaire 1 Entiers de 400 à 409 2 Entiers de 410 à 419 3 Entiers de 420 à 429 …   Wikipédia en Français

  • 600 (nombre) — Nombres 600 à 699 Cet article recense les nombres qui ont des propriétés remarquables allant de 600 à 699. Sommaire 1 Entiers de 600 à 609 2 Entiers de 610 à 619 3 Entiers de 620 à 629 4 Enti …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”