Nombre pentagonal

Nombre pentagonal
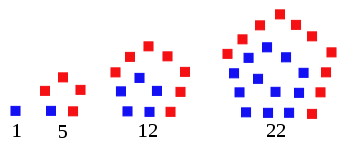
Nombre pentagon.svg

Un nombre pentagonal est un nombre figuré qui peut être représenté par un pentagone. Un nombre pentagonal de rang n est défini par

n(3n-1)\over 2

n étant un entier naturel non nul.

Sommaire

Exemples

Les premiers nombres pentagonaux sont

1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001

Les nombres pentagonaux sont importants dans la théorie des partages d'entiers d'Euler, et ils interviennent par exemple dans son théorème du nombre pentagonal.

Généralisation

Les nombres pentagonaux « généralisés » sont obtenus à partir de la formule donnée ci-dessus, mais avec n prenant les valeurs 0, 1, -1, 2, -2, 3, -3, 4..., produisant la suite

0, 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92, 100, 117, 126, 145, 155, 176, 187, 210, 222, 247, 260, 287, 301, 330, 345, 376, 392, 425, 442, 477, 495, 532, 551, 590, 610, 651, 672, 715, 737, 782, 805, 852, 876, 925, 950, 1001, 1027

Remarques

Le nombre pentagonal de rang n est égal à un tiers du nombre triangulaire de rang 3n - 1.

Les nombres pentagonaux ne devraient pas être confondus avec les nombres pentagonaux centrés.

Test des nombres pentagonaux

Pour savoir si un nombre entier x est un nombre pentagonal (non généralisé) on calcule le réel suivant:

n= \frac{\sqrt{24x+1}+1}6

Si n est entier alors x est le nème nombre pentagonal. Si n n'est pas entier alors x n'est pas un nombre pentagonal.

Voir aussi

Lien externe


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre pentagonal de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Nombre Pentagonal — Un nombre pentagonal est un nombre figuré qui peut être représenté par un pentagone. Un nombre pentagonal de rang n est défini par n étant un entier naturel non nul. Sommaire 1 Exemples …   Wikipédia en Français

  • Nombre Pentagonal Centré — Un nombre pentagonal centré est un nombre figuré centré qui peut être représenté par un pentagone ayant un point placé en son centre et tous les autres points disposés autour de ce centre formant des couches pentagonales successives. Pour tout… …   Wikipédia en Français

  • Nombre pentagonal centre — Nombre pentagonal centré Un nombre pentagonal centré est un nombre figuré centré qui peut être représenté par un pentagone ayant un point placé en son centre et tous les autres points disposés autour de ce centre formant des couches pentagonales… …   Wikipédia en Français

  • Nombre pentagonal centré — Un nombre pentagonal centré est un nombre figuré centré qui peut être représenté par un pentagone ayant un point placé en son centre et tous les autres points disposés autour de ce centre formant des couches pentagonales successives. Pour tout… …   Wikipédia en Français

  • Nombre pentagonal pyramidal — Nombre pyramidal pentagonal Un nombre pyramidal pentagonal est un nombre égal à la somme des premiers nombres pentagonaux. Les premiers nombres pyramidaux pentagonaux sont : 1, 6, 18, 40, 75, 126, 196, 288, 405, 550, 726, 936, 1183, 1470,… …   Wikipédia en Français

  • Theoreme du nombre pentagonal — Théorème du nombre pentagonal En mathématiques, le théorème du nombre pentagonal, dû originellement au mathématicien suisse Euler, établit que Ce théorème peut être donné comme une interprétation combinatoire en termes de partages. En particulier …   Wikipédia en Français

  • Théorème du nombre pentagonal — En mathématiques, le théorème du nombre pentagonal, dû originellement au mathématicien suisse Euler, établit que Ce théorème peut être donné comme une interprétation combinatoire en termes de partages. En particulier, le côté gauche est une… …   Wikipédia en Français

  • Nombre Triangulaire — Un nombre triangulaire est un nombre qui peut être représenté par un triangle équilatéral. Les premiers termes de la suite des nombres triangulaires (A000217 dans l encyclopédie électronique des suites entières) sont: 0, 1, 3, 6, 10, 15, 21, 28,… …   Wikipédia en Français

  • Nombre douze — 12 (nombre) « Douze » redirige ici. Cet article concerne le nombre 12. Pour l année, voir 12. Pour les autres significations, voir Douze (homonymie) …   Wikipédia en Français

  • Nombre Pyramidal Pentagonal — Un nombre pyramidal pentagonal est un nombre égal à la somme des premiers nombres pentagonaux. Les premiers nombres pyramidaux pentagonaux sont : 1, 6, 18, 40, 75, 126, 196, 288, 405, 550, 726, 936, 1183, 1470, 1800, 2176, 2601, 3078, 3610,… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”