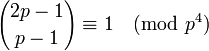Nombre De Wolstenholme
- Nombre De Wolstenholme
-
Nombre de Wolstenholme
En mathématiques, un nombre premier de Wolstenholme est une certaine catégorie de nombres premiers. Un nombre premier p est appelé nombre premier de Wolstenholme ssi la condition suivante reste valable :
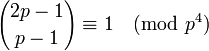
Les nombres premiers de Wolstenholme sont nommés en l'honneur du mathématicien Joseph Wolstenholme, qui a démontré le théorème de Wolstenholme, l'énoncé équivalent pour 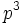 en 1862, en suivant Charles Babbage qui montra l'équivalent pour
en 1862, en suivant Charles Babbage qui montra l'équivalent pour 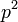 en 1819.
en 1819.
Les seuls nombres premiers de Wolstenholme connus sont 16843 et 2124679 (Encyclopédie électronique des suites entières (id=A088164) ; tout autre nombre premier de Wolstenholme doit être plus grand que  .
.
Liens internes
Liens externes
 Portail des mathématiques
Portail des mathématiques
Catégorie : Nombre premier
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Nombre De Wolstenholme de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Nombre de wolstenholme — En mathématiques, un nombre premier de Wolstenholme est une certaine catégorie de nombres premiers. Un nombre premier p est appelé nombre premier de Wolstenholme ssi la condition suivante reste valable : Les nombres premiers de Wolstenholme… … Wikipédia en Français
Nombre de Wolstenholme — En mathématiques, un nombre premier p est appelé nombre premier de Wolstenholme si la condition suivante est vérifiée : Les nombres premiers de Wolstenholme sont nommés en l honneur du mathématicien Joseph Wolstenholme, qui a démontré le… … Wikipédia en Français
Nombre De Wieferich — En mathématiques, un nombre premier de Wieferich est un nombre premier p tel que divise , comparer ceci avec le petit théorème de Fermat, qui énonce que chaque nombre premier p divise . Les nombres premiers de Wieferich furent décrits en premier… … Wikipédia en Français
Nombre de wieferich — En mathématiques, un nombre premier de Wieferich est un nombre premier p tel que divise , comparer ceci avec le petit théorème de Fermat, qui énonce que chaque nombre premier p divise . Les nombres premiers de Wieferich furent décrits en premier… … Wikipédia en Français
Nombre De Wall-Sun-Sun — En mathématiques, un nombre premier de Wall Sun Sun est une certaine catégorie de nombre premier. Un nombre premier p > 5 est appelé un nombre premier de Wall Sun Sun si p2 divise , où F(n) est le n ième nombre de Fibonacci et est le symbole… … Wikipédia en Français
Nombre De Wilson — En mathématiques, un nombre premier de Wilson est une certaine catégorie de nombre premier. Un nombre premier p est appelé un nombre premier de Wilson si divise , où ! désigne la fonction factorielle ; comparer ceci avec le théorème de… … Wikipédia en Français
Nombre de wall-sun-sun — En mathématiques, un nombre premier de Wall Sun Sun est une certaine catégorie de nombre premier. Un nombre premier p > 5 est appelé un nombre premier de Wall Sun Sun si p2 divise , où F(n) est le n ième nombre de Fibonacci et est le symbole… … Wikipédia en Français
Nombre de wilson — En mathématiques, un nombre premier de Wilson est une certaine catégorie de nombre premier. Un nombre premier p est appelé un nombre premier de Wilson si divise , où ! désigne la fonction factorielle ; comparer ceci avec le théorème de… … Wikipédia en Français
Nombre de Wieferich — En mathématiques, un nombre premier de Wieferich est un nombre premier p tel que divise , comparer ceci avec le petit théorème de Fermat, qui énonce que chaque nombre premier p divise . Les nombres premiers de Wieferich furent décrits en premier… … Wikipédia en Français
Nombre de Wall-Sun-Sun — En mathématiques, un nombre premier de Wall Sun Sun est une certaine catégorie de nombre premier. Un nombre premier p > 5 est appelé un nombre premier de Wall Sun Sun si p2 divise , où F(n) est le n ième nombre de Fibonacci et est le symbole… … Wikipédia en Français
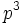 en 1862, en suivant Charles Babbage qui montra l'équivalent pour
en 1862, en suivant Charles Babbage qui montra l'équivalent pour 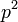 en 1819.
en 1819. .
.