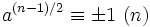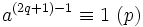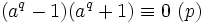Nombre Pseudopremier D'Euler

Nombre pseudopremier d'Euler

En mathématiques et plus précisément en arithmétique modulaire un nombre pseudopremier d'Euler désigne un nombre entier particulier.

Un nombre impair composé n est appelé un pseudopremier d'Euler de base a, si a et n sont premiers entre eux, et

$a^{(n-1)/2} \equiv \pm 1\ (n)$

(égalité de congruence modulo n).

Cette définition est motivée par le fait que tous les nombres premiers p satisfont à la relation ci-dessus, ce qui peut être démontré à partir du petit théorème de Fermat. Le théorème de Fermat établit que si p est premier, et premier avec a, alors

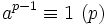$a^{p-1} \equiv 1 \ (p)$ .

Supposons que p > 2 soit premier, alors p peut être exprimé sous la forme 2q+1 où q est un entier. Ainsi

$a^{(2q+1)-1} \equiv 1 \ (p)$

ce qui veut dire que

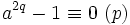$a^{2q} - 1 \equiv 0 \ (p)$ .

D'où en factorisant le premier membre

$(a^{q} - 1)(a^{q} + 1) \equiv 0 \ (p)$

ce qui est équivalent à

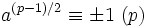$a^{(p-1)/2} \equiv \pm 1 \ (p)$ .

La relation peut être vérifiée plutôt rapidement, ce qui est utilisé pour les tests de primalité. Ces tests sont deux fois plus forts que les tests basés sur le petit théorème de Fermat.

Chaque pseudopremier d'Euler est aussi un pseudopremier de Fermat. Il n'est pas possible de produire un test définitif de primalité basé sur l'éventualité qu'un nombre soit un pseudopremier d'Euler parce qu'il existe des nombres pseudopremiers absolus d'Euler, qui sont des pseudopremiers d'Euler pour chaque base relativement première à elles-mêmes. Les pseudopremiers absolus d'Euler sont un sous-ensemble des pseudopremiers de Fermat absolus, ou nombres de Carmichaël, le plus petit pseudopremier absolu d'Euler est 1729 = 7×13×19.

Il devrait être noté que la condition plus forte

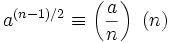
$a^{(n-1)/2} \equiv \left(\frac{a}{n}\right) \ (n)$

où pgcd(a,n)=1 et $\left(\frac{a}{n}\right)$ est le symbole de Jacobi, est quelque fois utilisée pour une définition d'un pseudopremier d'Euler. Une discussion sur les nombres de cette forme peut être trouvée sur l'article nombre pseudopremier d'Euler-Jacobi.

Voir aussi

Nombre premier probable

Portail des mathématiques

Ce document provient de « Nombre pseudopremier d%27Euler ».

Catégories : Test de primalité | Nombre premier

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre Pseudopremier D'Euler de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Nombre pseudopremier d'euler — En mathématiques et plus précisément en arithmétique modulaire un nombre pseudopremier d Euler désigne un nombre entier particulier. Un nombre impair composé n est appelé un pseudopremier d Euler de base a, si a et n sont premiers entre eux, et… … Wikipédia en Français
Nombre pseudopremier d'Euler — En mathématiques et plus précisément en arithmétique modulaire un nombre pseudopremier d Euler désigne un nombre entier particulier. Un nombre impair composé n est appelé un pseudopremier d Euler de base a, si a et n sont premiers entre eux, et… … Wikipédia en Français
Nombre Pseudopremier D'Euler-Jacobi — Un nombre entier impair composé n est appelé pseudopremier d Euler Jacobi de base a, si a et n sont premiers entre eux, et où est le symbole de Jacobi. Cette définition est motivée par le fait que tous les nombres premiers n satisfont l équation… … Wikipédia en Français
Nombre pseudopremier d'euler-jacobi — Un nombre entier impair composé n est appelé pseudopremier d Euler Jacobi de base a, si a et n sont premiers entre eux, et où est le symbole de Jacobi. Cette définition est motivée par le fait que tous les nombres premiers n satisfont l équation… … Wikipédia en Français
Nombre pseudopremier d'Euler-Jacobi — Un nombre entier impair composé n est appelé pseudopremier d Euler Jacobi de base a, si a et n sont premiers entre eux, et où est le symbole de Jacobi. Cette définition est motivée par le fait que tous les nombres premiers n satisfont l équation… … Wikipédia en Français
Nombre Pseudopremier — Un nombre pseudopremier est un nombre premier probable (un entier qui partage une propriété commune à tous les nombres premiers) qui n est pas premier. Les nombres pseudopremiers peuvent être classés par rapport à la propriété qu ils satisfont.… … Wikipédia en Français
Pseudopremier d'Euler — Nombre pseudopremier d Euler En mathématiques et plus précisément en arithmétique modulaire un nombre pseudopremier d Euler désigne un nombre entier particulier. Un nombre impair composé n est appelé un pseudopremier d Euler de base a, si a et n… … Wikipédia en Français
Pseudopremier d'Euler-Jacobi — Nombre pseudopremier d Euler Jacobi Un nombre entier impair composé n est appelé pseudopremier d Euler Jacobi de base a, si a et n sont premiers entre eux, et où est le symbole de Jacobi. Cette définition est motivée par le fait que tous les… … Wikipédia en Français
Nombre pseudopremier — Un nombre pseudopremier est un nombre premier probable (un entier qui partage une propriété commune à tous les nombres premiers) qui n est pas premier. Les nombres pseudopremiers peuvent être classés par rapport à la propriété qu ils satisfont.… … Wikipédia en Français
Pseudopremier — Nombre pseudopremier Un nombre pseudopremier est un nombre premier probable (un entier qui partage une propriété commune à tous les nombres premiers) qui n est pas premier. Les nombres pseudopremiers peuvent être classés par rapport à la… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Nombre Pseudopremier D'Euler