- Nombre pseudopremier d'euler-jacobi
-
Nombre pseudopremier d'Euler-Jacobi
Un nombre entier impair composé n est appelé pseudopremier d'Euler-Jacobi de base a, si a et n sont premiers entre eux, et
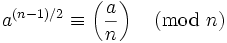
où
 est le symbole de Jacobi.
est le symbole de Jacobi.Cette définition est motivée par le fait que tous les nombres premiers n satisfont l'équation précédente, comme expliqué dans l'article du symbole de Legendre. L'équation peut être testée plutôt rapidement, qui peut être utilisée pour les tests de primalité probabilistes. Ces tests sont plus de deux fois plus forts que les tests basés sur le petit théorème de Fermat.
Chaque pseudopremier d'Euler-Jacobi est aussi un pseudopremier de Fermat et un pseudopremier d'Euler. Il n'existe pas de nombre qui est pseudopremier d'Euler-Jacobi pour toutes les bases de la même manière que les nombres de Carmichael. Solovay et Strassen ont montré que pour chaque composé n, pour au moins n/2 bases inférieures à n, n n'est pas un pseudopremier d'Euler-Jacobi.
Il devrait être noté que ces nombres sont, dans certaines sources, appelés pseudopremiers d'Euler.
La table ci-dessous donne tous les pseudopremiers d'Euler-Jacobi inférieurs à 10 000 pour certaines bases premières a, cette table est en cours de vérification et doit être utilisée avec précaution jusqu'à ce que cette notice soit enlevée.
a 2 561, 1105, 1729, 1905, 2047, 2465, 3277, 4033, 4681, 6601, 8321, 8481 3 121, 1729, 2821, 7381, 8401 5 781, 1541, 1729, 5461, 5611, 6601, 7449 7 25, 703, 2101, 2353, 2465, 3277 11 133, 793, 2465, 4577, 4921, 5041, 5185 13 105, 1785, 5149, 7107, 8841, 9577, 9637 17 9, 145, 781, 1305, 2821, 4033, 5833, 6697 19 9, 45, 49, 169, 1849, 2353, 3201, 4033, 4681, 6541, 6697, 8281 23 169, 265, 553, 1729, 2465, 4033, 4681, 6533, 6541, 7189, 8321, 8911 29 91, 341, 469, 871, 2257, 5149, 5185, 6097, 8401, 8841 31 15, 49, 133, 481, 2465, 6241, 7449, 9131 37 9, 451, 469, 589, 817, 1233, 1333, 1729, 3781, 3913, 4521, 5073, 8905, 9271 41 21, 105, 841, 1065, 1281, 1417, 2465, 2701, 3829, 8321 43 21, 25, 33, 77, 105, 185, 385, 481, 561, 777, 825, 973, 1105, 1541, 1729,
1825, 2465, 2553, 2821, 2849, 3281, 3439, 3781, 4033, 4417, 6105, 6369, 6545, 6601, 6697, 7825,
47 65, 69, 341, 345, 481, 561, 703, 721, 793, 897, 1105, 1649, 1729, 1891, 2257, 2465, 2737, 3145,
3201, 5185, 5461, 5865, 6305, 9361
53 9, 65, 91, 117, 561, 585, 1105, 1441, 1541, 1729, 2209, 2465, 2529, 2821, 2863, 3097, 3367,
3481, 3861, 5317, 5833, 6031, 6433, 9409
59 145, 451, 561, 645, 1105, 1141, 1247, 1541, 1661, 1729, 1991, 2413, 2465, 3097, 4681, 5611, 5729,
6191, 6533, 6601, 7421, 8149, 8321, 8705, 9637
61 15, 93, 217, 341, 465, 1261, 1441, 1729, 2465, 2821, 3565, 3661, 4061, 4577,
5461, 6541, 6601, 6697, 7613, 7905, 9305, 9937
67 33, 49, 217, 385, 561, 1105, 1309, 1519, 1705, 1729, 2209, 2465, 3201, 5797, 7633, 7701,
8029, 8321, 8371, 9073
Voir aussi :
- Portail des mathématiques
Catégorie : Test de primalité
Wikimedia Foundation. 2010.
