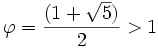Nombre De Pisot-Vijayaraghavan

Nombre de Pisot-Vijayaraghavan

En mathématiques, un nombre de Pisot-Vijayaraghavan est un entier algébrique réel supérieur à 1, dont tous les éléments conjugués ont un module strictement inférieur à 1. Par exemple, le nombre entier quadratique 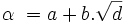$\alpha\ = a + b.\sqrt d\,$ , où a et b sont tous deux des entiers ou la moitié d'un entier impair, admet un conjugué 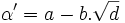$\alpha' = a - b.\sqrt d\,$ ; les conditions sont alors :

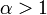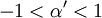$\alpha > 1\,$ et $- 1< \alpha' < 1\,$ .

Ces conditions sont satisfaites par le nombre d'or 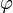$\varphi\,$ . Nous avons alors :

$\varphi = \frac{(1 + \sqrt5)}{2} > 1\,$

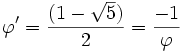$\varphi' = \frac{(1 - \sqrt5)}{2} = \frac{-1}{\varphi}\,$ .

La condition générale fut étudiée par G. H. Hardy en relation avec un problème d'approximation diophantienne. Ce travail fut rejoint par Tirukkannapuram Vijayaraghavan (30 novembre 1902 - 20 avril 1955), un mathématicien indien de la région de Madras qui vint à Oxford pour travailler avec Hardy dans le milieu des années 1920. La même condition apparaît aussi dans certains problèmes sur les séries de Fourier et fut étudiée plus tard par Charles Pisot. Le nom, formé par ces deux auteurs, est maintenant communément en usage.

Les nombres de Pisot-Vijayaraghavan peuvent être utilisés pour engendrer presque tous les entiers : la nième puissance d'un nombre de Pisot "approche les entiers" quand n tend vers l'infini. Par exemple, 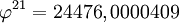$\varphi^{21} = 24476,0000409$ . L'effet peut même être plus prononcé pour les nombres de Pisot-Vijayaraghavan engendrés à partir d'équations de degré plus élevé.

Cette propriété provient du fait que pour chaque n, la somme des nièmes puissances d'un entier algébrique x et de son conjugué est exactement un entier ; lorsque x est un nombre de Pisot, les nièmes puissances des (autres) conjugués tendent vers 0 quand n tend vers l'infini.

Le plus petit nombre de Pisot-Vijayaraghavan est l'unique racine réelle du polynome 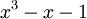$x^3 - x - 1\,$ , connu sous le nom de nombre plastique ou nombre d'argent (approximativement 1,324718).

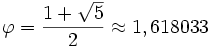Le plus petit point d'accumulation de l'ensemble des nombres de Pisot-Vijayaraghavan est le nombre d'or $\varphi = \frac{1 + \sqrt 5}{2} \approx 1,618033$ .

Table des nombres de Pisot

Voici les 38 nombres de Pisot inférieurs à 1,618, en ordre croissant.

	Valeur	Racine de...
1	1,3247179572447460260	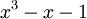$x^3-x-1\,$
2	1,3802775690976141157	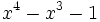$x^4-x^3-1\,$
3	1,4432687912703731076	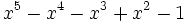$x^5-x^4-x^3+x^2-1\,$
4	1,4655712318767680267	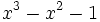$x^3-x^2-1\,$
5	1,5015948035390873664	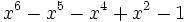$x^6-x^5-x^4+x^2-1\,$
6	1,5341577449142669154	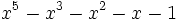$x^5-x^3-x^2-x-1\,$
7	1,5452156497327552432	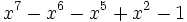$x^7-x^6-x^5+x^2-1\,$
8	1,5617520677202972947	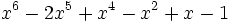$x^6-2x^5+x^4-x^2+x-1\,$
9	1,5701473121960543629	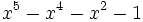$x^5-x^4-x^2-1\,$
10	1,5736789683935169887	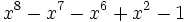$x^8-x^7-x^6+x^2-1\,$
11	1,5900053739013639252	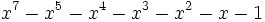$x^7-x^5-x^4-x^3-x^2-x-1\,$
12	1,5911843056671025063	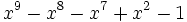$x^9-x^8-x^7+x^2-1\,$
13	1,6013473337876367242	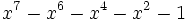$x^7-x^6-x^4-x^2-1\,$
14	1,6017558616969832557	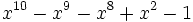$x^{10}-x^9-x^8+x^2-1\,$
15	1,6079827279282011499	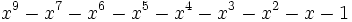$x^9-x^7-x^6-x^5-x^4-x^3-x^2-x-1\,$
16	1,6081283851873869594	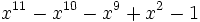$x^{11}-x^{10}-x^9+x^2-1\,$
17	1,6119303965641198198	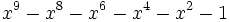$x^9-x^8-x^6-x^4-x^2-1\,$
18	1,6119834212464921559	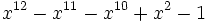$x^{12}-x^{11}-x^{10}+x^2-1\,$
19	1,6143068232571485146	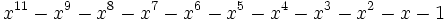$x^{11}-x^9-x^8-x^7-x^6-x^5-x^4-x^3-x^2-x-1\,$
20	1,6143264149391271041	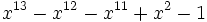$x^{13}-x^{12}-x^{11}+x^2-1\,$
21	1,6157492027552106107	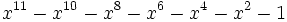$x^{11}-x^{10}-x^8-x^6-x^4-x^2-1\,$
22	1,6157565175408433755	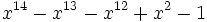$x^{14}-x^{13}-x^{12}+x^2-1\,$
23	1,6166296843945727036	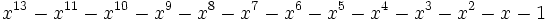$x^{13}-x^{11}-x^{10}-x^9-x^8-x^7-x^6-x^5-x^4-x^3-x^2-x-1\,$
24	1,6166324353879050082	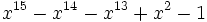$x^{15}-x^{14}-x^{13}+x^2-1\,$
25	1,6171692963550925635	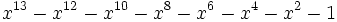$x^{13}-x^{12}-x^{10}-x^8-x^6-x^4-x^2-1\,$
26	1,6171703361720168476	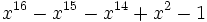$x^{16}-x^{15}-x^{14}+x^2-1\,$
27	1,6175009054313240144	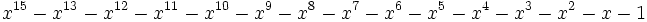$x^{15}-x^{13}-x^{12}-x^{11}-x^{10}-x^9-x^8-x^7-x^6-x^5-x^4-x^3-x^2-x-1\,$
28	1,6175012998129095573	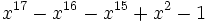$x^{17}-x^{16}-x^{15}+x^2-1\,$
29	1,6177050699575566445	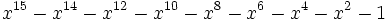$x^{15}-x^{14}-x^{12}-x^{10}-x^8-x^6-x^4-x^2-1\,$
30	1,6177052198884550971	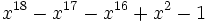$x^{18}-x^{17}-x^{16}+x^2-1\,$
31	1,6178309287889738637	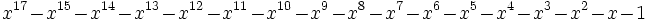$x^{17}-x^{15}-x^{14}-x^{13}-x^{12}-x^{11}-x^{10}-x^9-x^8-x^7-x^6-x^5-x^4-x^3-x^2-x-1\,$
32	1,6178309858778122988	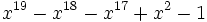$x^{19}-x^{18}-x^{17}+x^2-1\,$
33	1,6179085817671650120	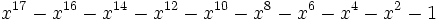$x^{17}-x^{16}-x^{14}-x^{12}-x^{10}-x^8-x^6-x^4-x^2-1\,$
34	1,6179086035278053858	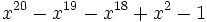$x^{20}-x^{19}-x^{18}+x^2-1\,$
35	1,6179565199535642392	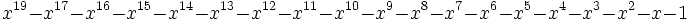$x^{19}-x^{17}-x^{16}-x^{15}-x^{14}-x^{13}-x^{12}-x^{11}-x^{10}-x^9-x^8-x^7-x^6-x^5-x^4-x^3-x^2-x-1\,$
36	1,6179565282539765702	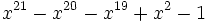$x^{21}-x^{20}-x^{19}+x^2-1\,$
37	1,6179861253852491516	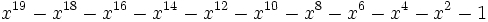$x^{19}-x^{18}-x^{16}-x^{14}-x^{12}-x^{10}-x^8-x^6-x^4-x^2-1\,$
38	1,6179861285528618287	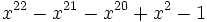$x^{22}-x^{21}-x^{20}+x^2-1\,$

Voir aussi

nombre de Salem

Liens externes

nombre de Pisot, Encyclopedia of Mathematics [1]
nombre de Pisot, Mathworld [2]

Références

M.J. Bertin, A. Decomps-Guilloux, M. Grandet-Hugot, M. Pathiaux-Delefosse, J.P. Schreiber, "Pisot and Salem Numbers", Birkhäuser (1992)
D.W. Boyd, "Pisot and Salem numbers in intervals of the real line" Math. Comp., 32 (1978) pp. 1244–1260

Portail des mathématiques

Ce document provient de « Nombre de Pisot-Vijayaraghavan ».

Catégories : Propriété numérique | Théorie algébrique des nombres

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre De Pisot-Vijayaraghavan de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Nombre de pisot-vijayaraghavan — En mathématiques, un nombre de Pisot Vijayaraghavan est un entier algébrique réel supérieur à 1, dont tous les éléments conjugués ont un module strictement inférieur à 1. Par exemple, le nombre entier quadratique , où a et b sont tous deux des… … Wikipédia en Français
Nombre de Pisot-Vijayaraghavan — En mathématiques, un nombre de Pisot Vijayaraghavan est un entier algébrique réel strictement supérieur à 1, dont tous les éléments conjugués (en) ont un module strictement inférieur à 1. Par exemple, le nombre entier quadratique , où a et b … Wikipédia en Français
Número de Pisot-Vijayaraghavan — En matemáticas, un número de Pisot Vijayaraghavan (también conocido simplemente como número de Pisot o número de PV), es un entero algebraico que es real mayor que 1, pero sus elementos conjugados son todos menores que 1 en valor absoluto. Por… … Wikipedia Español
Nombre Plastique — Le nombre plastique, de symbole ψ (à lire psi), est l unique solution réelle de l équation d ordre 3 : ψ3 = 1 + ψ et qui s exprime par : C est un nombre algébrique irrationnel. À l instar du nombre d or, il est à la base d un système de … Wikipédia en Français
Nombre radiant — Nombre plastique Le nombre plastique, de symbole ψ (à lire psi), est l unique solution réelle de l équation d ordre 3 : ψ3 = 1 + ψ et qui s exprime par : C est un nombre algébrique irrationnel. À l instar du nombre d or, il est à la… … Wikipédia en Français
Nombre Algébrique — Un nombre algébrique, en mathématiques, est tout nombre qui est solution d une équation algébrique (autrement dit racine d un polynôme différent de zéro) à coefficients entiers (ou de manière équivalente, à coefficients rationnels). Sans plus de… … Wikipédia en Français
Nombre algebrique — Nombre algébrique Un nombre algébrique, en mathématiques, est tout nombre qui est solution d une équation algébrique (autrement dit racine d un polynôme différent de zéro) à coefficients entiers (ou de manière équivalente, à coefficients… … Wikipédia en Français
Nombre D'argent — L appellation nombre d argent a été proposée pour diverses généralisations du nombre d or ; elles sont encore en concurrence actuellement. Sommaire 1 Première proposition 2 Deuxième proposition 3 Troisième proposition … Wikipédia en Français
Nombre De Salem — Pour les articles homonymes, voir Salem. En mathématiques, un entier algébrique réel est un nombre de Salem si tous ses conjugués ont un module inférieur ou égal à 1, et au moins un conjugué a un module égal à 1. Les nombres de Salem apparaissent … Wikipédia en Français
Nombre de salem — Pour les articles homonymes, voir Salem. En mathématiques, un entier algébrique réel est un nombre de Salem si tous ses conjugués ont un module inférieur ou égal à 1, et au moins un conjugué a un module égal à 1. Les nombres de Salem apparaissent … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Nombre De Pisot-Vijayaraghavan