Approximation de Boussinesq

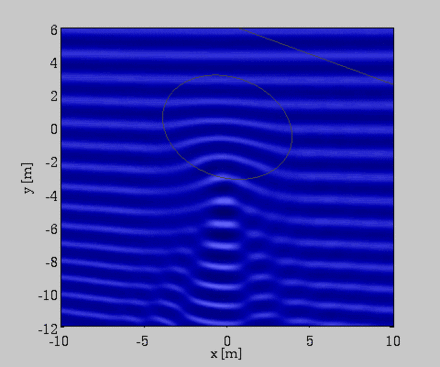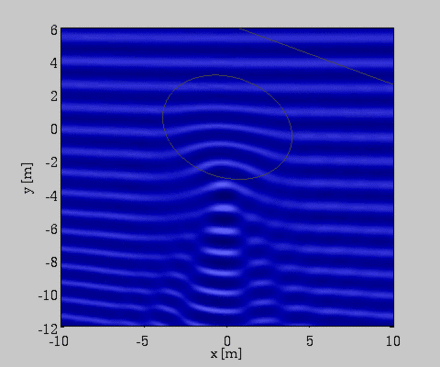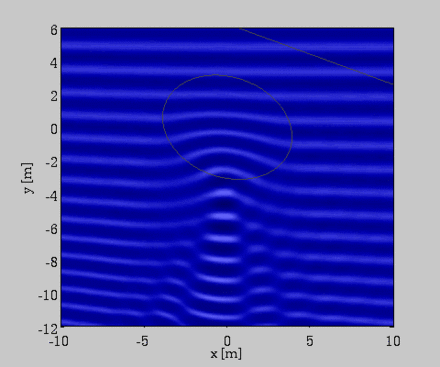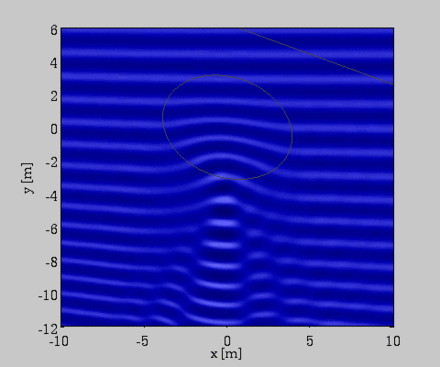Approximation de Boussinesq: Propagation d'une onde de gravité sur un banc de sable sous marin de forme elliptique - Modélisation par approximation de Boussinesq

En dynamique des fluides, l'approximation de Boussinesq, nommée en l'honneur de Joseph Boussinesq, est utilisée dans les équations de modification des fluides pour négliger les forces de compression excepté pour calculer les forces de flottabilité hydrostatique. L'approximation prend ainsi comme hypothèse que les fluides ont une masse volumique constante qui ne dépend que de sa température si l'on considère que la dimension horizontale est beaucoup plus grande que celle verticale. Dans le cas où on retrouve deux fluides de densités différentes en contact, g, la constante de gravité locale, exerce une force vers le bas différente selon la densité de chaque fluide et mène à leur stratification.

Les flux obéissant à l'approximation de Boussinesq sont fréquents dans la nature : zones frontales entre les masses d'air, zones de discontinuité océaniques, vents catabatiques, dispersion des gaz polluants denses et ventilation, climatisation, etc., ce qui rend les calculs physiques plus simples. Par contre, les ondes sonores n'obéissent pas à cette approximation puisqu'elles sont issues de la compression du milieu, donc de variations de masse volumique.

Sommaire

1 Principe

2 Utilisation

2.1 Inversion

3 Flux non-Boussinesq

4 Voir aussi

5 Liens externes

Principe

Joseph Boussinesq

Article détaillé : Équations de Navier-Stokes.

La formulation différentielle des équations de masse et de mouvement qui régissent les fluides est donnée par :

Équation de continuité (ou équation de bilan de la masse) $\frac{\partial \rho}{\partial t} + \overrightarrow{\nabla} \cdot (\rho \vec{v}) = 0$

Équation de bilan de la quantité de mouvement $\frac{\partial \left( \rho \vec{v} \right)}{\partial t} + \overrightarrow{\nabla} \cdot \left(\rho \vec{v} \otimes \vec{v} \right) = - \overrightarrow{\nabla} p + \overrightarrow{\nabla} \cdot \overrightarrow{\overrightarrow {\tau}} + \rho \vec{f}$

Dans ces équations :

$t$ représente le temps (unité SI : $s$ ) ;

$ρ$ désigne la masse volumique du fluide (unité SI : $k g . m - 3$ ) ;

$\vec{v} = ( v_1, v_2, v_3 )$ désigne la vitesse eulérienne d'une particule fluide (unité SI : $m.s - 1$ ) ;

$p$ désigne la pression (unité SI : $Pa$ ) ;

$\overrightarrow{\overrightarrow{\tau}} = \left( \tau_{i,j} \right)_{i,j}$ est le tenseur des contraintes visqueuses (unité SI : $Pa$ ) ;

$\vec{f}$ désigne la résultante des forces massiques s'exerçant dans le fluide (unité SI : $N.kg - 1$ ) ;

On voit que chacune de ces deux équations comporte la variable $\,\rho$ . Si la variation de celle-ci est négligeable, dans le temps et l'espace dans un volume, les équations seront grandement simplifiée car :

$\, \frac{\partial \rho}{\partial t} = 0$

$\overrightarrow{\nabla} \rho = 0$

Et laisse les équations :

Équation de continuité appelée alors équation d'incompressibilité $\overrightarrow{\nabla} \cdot \vec{v}= 0$

Équation de bilan de la quantité de mouvement $\frac{\partial \vec{v}}{\partial t} + \left( \vec{v} \cdot \overrightarrow{\nabla} \right) \vec{v} = - \frac{1}{\rho} \overrightarrow{\nabla} p + \nu \nabla^2 \vec{v}+ \vec{f}$

où $\nu = \tfrac{\mu}{\rho}$ désigne la viscosité cinématique du fluide (unité SI : $m 2 .s - 1$ )

Dans ces dernières, le seul endroit où la masse volumique subsiste est dans $\frac{1}{\rho} \overrightarrow{\nabla} p$ et $ν$ . Or $\overrightarrow{\nabla}p$ dépend de $\overrightarrow g$ (la constante de gravité) selon l'équilibre hydrostatique.

Utilisation

Si on peut négliger les variations de la masse volumique entre deux fluides, la seule force qui s'exercera sera celle de la gravité. En effet, la variation de $ν$ par la variation de densité dû au changement de température horizontale est très minime dans la plupart des fluides. L'approximation de Boussinesq est donc acceptable dans la plupart des situations à large échelle en météorologie et océanographie.

Supposons deux fluides ayant des densités $ρ 1$ et $ρ 2$ alors que $Δρ = ρ 1 - ρ 2$ est négligeable.

On peut alors utiliser un $\bar \rho$ pour les décrire. Dans cette situation, la force hydrostatique sera :

$g' = g{\rho_1-\rho_2\over {\bar \rho}}$ .

Onde de surface type Boussinesq sur une couche fluide

Exemple : une vague scélérate est une vague océanique très haute, modélisable comme solution particulière d’équations non linéaires, telles que l’équation de l’onde de Boussinesq ou l’équation de Korteweg et de Vries.

Inversion

Un des avantages de cette approximation est que les équations restent les mêmes dans le fluide supérieur et inférieur. Par exemple, dans une pièce chaude dont les fenêtres sont ouvertes sur un environnement plus frais, l'air moins dense de la pièce monte au plafond et l'air extérieur plus dense entre et se dirige vers le plancher. Dans la situation inverse, une chambre froide dans un environnement chaud, l'air chaud extérieur entre dans la chambre et se retrouve au plafond alors que l'air frais de la pièce demeure au sol. Si on est dans des conditions d'approximation de Boussinesq, ces deux situations sont similaires mais miroirs et les équations qui s'appliquent pour l'une sont les mêmes pour l'autre, à un signe négatif près (selon l'équation de $g'$ ).

Flux non-Boussinesq

Un exemple où l'approximation ne s'applique pas est celui de bulles d'air chaud s'élevant dans un liquide. Celles-ci prendront la forme de sphères. Par contre, des gouttes d'eau tombant dans l'air prendront une forme oblongue et se briseront souvent en plus petites gouttes. Il n'y a pas de réciprocité dans ces deux cas, car la tension superficielle de l'eau s'ajoute à l'équation du comportement des bulles.

Voir aussi

Joseph Boussinesq

Nombre de Boussinesq

Liens externes

Joseph Boussinesq and his approximation: a contemporary view, R.Kh. Zeytounian, Comptes Rendus Mécanique; Volume 331, numéro 8,pages 575-586 (août 2003).

Portail de la physique

Portail de la météorologie

Catégories :
Mécanique des fluides
Théorie météorologique

Contenu soumis à la licence CC-BY-SA. Source : Article Approximation de Boussinesq de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Approximation De Boussinesq — Propagation d ondes sur un banc de sable sous marin de forme elliptique Modélisation par approximation de Boussinesq En dynamique des fluides, l approximation de Boussinesq, nommée en l honneur de Joseph Boussinesq, est utilisée dans les… … Wikipédia en Français
Approximation de boussinesq — Propagation d ondes sur un banc de sable sous marin de forme elliptique Modélisation par approximation de Boussinesq En dynamique des fluides, l approximation de Boussinesq, nommée en l honneur de Joseph Boussinesq, est utilisée dans les… … Wikipédia en Français
Boussinesq approximation — may refer to: * Boussinesq approximation (buoyancy) for buoyancy driven flows for small density differences in the fluid * Boussinesq approximation (water waves) for long waves propagating on the surface of a fluid layer under the action of… … Wikipedia
Boussinesq approximation (water waves) — In fluid dynamics, the Boussinesq approximation for water waves is an approximation valid for weakly non linear and fairly long waves. The approximation is named after Joseph Boussinesq, who first derived them in response to the observation by… … Wikipedia
Boussinesq approximation (buoyancy) — In fluid dynamics, the Boussinesq approximation (named for Joseph Valentin Boussinesq) is used in the field of buoyancy driven flow (also known as natural convection). It states that density differences are sufficiently small to be neglected,… … Wikipedia
Boussinesq — Valentin Joseph Boussinesq Valentin Joseph Boussinesq (* 13. März 1842 in Saint André de Sangonis (Département Hérault), † 19. Februar 1929 in Paris) war ein französischer Mathematiker und Physiker. Leben und Wirken Joseph Boussinesq promovierte… … Deutsch Wikipedia
Boussinesq-Approximation — Die Boussinesq Approximation (nach Valentin Joseph Boussinesq) ist eine Vereinfachung der hydrodynamischen Navier Stokes Gleichungen. Sie modelliert gravitationsabhängige Strömungen, bei denen Dichtevariationen vernachlässigt werden können… … Deutsch Wikipedia
Joseph Boussinesq — Naissance 13 mars 1842 Saint André de Sangonis (France) Décès 19 février 1929 Paris (France) Nationalité … Wikipédia en Français
Joseph Valentin Boussinesq — (born March 13 1842 in Saint André de Sangonis (Hérault département ), died February 19 1929 in Paris) was a French mathematician and physicist who made significant contributions to the theory of hydrodynamics, vibration, light, and heat.John… … Wikipedia
Joseph Boussinesq — Valentin Joseph Boussinesq Valentin Joseph Boussinesq (* 13. März 1842 in Saint André de Sangonis (Département Hérault), † 19. Februar 1929 in Paris) war ein französischer Mathematiker und Physiker. Leben und Wirken Joseph Boussinesq promovierte… … Deutsch Wikipedia

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts