Méthode de Monte-Carlo

Pour les articles homonymes, voir Monte-Carlo (homonymie).

Le terme méthode de Monte-Carlo, ou méthode Monte-Carlo, désigne toute méthode visant à calculer une valeur numérique en utilisant des procédés aléatoires, c'est-à-dire des techniques probabilistes. Le nom de ces méthodes, qui fait allusion aux jeux de hasard pratiqués à Monte-Carlo, a été inventé en 1947 par Nicholas Metropolis^[1], et publié pour la première fois en 1949 dans un article co-écrit avec Stanislas Ulam^[2].

Les méthodes de Monte-Carlo sont particulièrement utilisées pour calculer des intégrales en dimensions plus grandes que 1 (en particulier, pour calculer des surfaces et des volumes). Elles sont également couramment utilisées en physique des particules, où des simulations probabilistes permettent d'estimer la forme d'un signal ou la sensibilité d'un détecteur. La comparaison des données mesurées à ces simulations peut permettre de mettre en évidence des caractéristiques inattendues, par exemple de nouvelles particules.

La méthode de simulation de Monte-Carlo permet aussi d'introduire une approche statistique du risque dans une décision financière. Elle consiste à isoler un certain nombre de variables-clés du projet, tels que le chiffre d'affaires ou la marge, et à leur affecter une distribution de probabilités. Pour chacun de ces facteurs, un grand nombre de tirages aléatoires est effectué dans les distributions de probabilité déterminées précédemment, afin de trouver la probabilité d'occurrence de chacun des résultats.

Le véritable développement des méthodes de Monte-Carlo s'est effectué sous l'impulsion de John von Neumann et Stanislas Ulam notamment, lors de la Seconde Guerre mondiale et des recherches sur la fabrication de la bombe atomique. Notamment, ils ont utilisé ces méthodes probabilistes pour résoudre des équations aux dérivées partielles dans le cadre de la Monte-Carlo N-Particle transport (MCNP).

Théorie

Nous disposons de l'expression de l'espérance mathématique d'une fonction $g$ de variable aléatoire $X$ , résultant du théorème de transfert, selon lequel

$G = E(g(X))=\int g(x)f_X(x) \, \mbox{d}x$

où $f X$ est une fonction de densité sur le support $[a; b]$ . Il est fréquent de prendre une distribution uniforme sur $[a; b]$ :

$f_X(x) = \frac{1}{b-a}$

Ceci peut être étendu aux probabilités discrètes en sommant grâce à une mesure $ν$ discrète, de type Dirac.

L'idée est de produire un échantillon $(x 1, x 2,..., x N)$ de la loi $X$ (donc d'après la densité $f X$ ) sur le support $[a; b]$ , et de calculer un nouvel estimateur dit de Monte-Carlo, à partir de cet échantillon.

La loi des grands nombres suggère de construire cet estimateur à partir de la moyenne empirique :

$\tilde{g_N} = \frac{1}{N} \sum_{i=1}^{N} g(x_i),$

qui se trouve être, par ailleurs, un estimateur sans biais de l'espérance.

Ceci est l'estimateur de Monte-Carlo. Nous voyons bien qu'en remplaçant l'échantillon par un ensemble de valeurs prises dans le support d'une intégrale, et de la fonction à intégrer, nous pouvons donc construire une approximation de sa valeur, construite statistiquement.

Cette estimation est sans biais, dans le sens où

$E(\tilde{g_N})= G = E(g(X))$

Il faut aussi quantifier la précision de cette estimation, via la variance de

$\tilde{g_N}$ .

Si l'échantillon est supposé iid, cette variance est estimée à l'aide de la variance empirique

$S^2_{g(X)} = \frac{1}{N} \sum_{i=1}^N (g(x_i) - \tilde{g_N})^2 \simeq \sigma_g^2$

avec

$\sigma_g^2= E(g^2(X)) - E(g(X))^2 = \int_{\Omega} g^2(x) f_X(x) \,\mbox{d} x - G^2$

Par le théorème de la limite centrale, on sait que la variable :

$Z := \frac{\tilde{g_N}-G}{\sigma_g / \sqrt{N}} \equiv \mathcal{N} \; \left(0;1\right)$

qui est centrée et réduite, suit approximativement la loi normale centrée réduite, ou loi de Gauss. Il est alors possible de construire des intervalles de confiance, ce qui permet d'encadrer l'erreur commise en remplaçant G par $\tilde{g_N}$ . Si cette erreur est dénotée $e n$ , alors pour un niveau de risque $α$ donné, on a:

$|e_n| \leq z_{1-\alpha/2}\frac{\sigma_g}{\sqrt{N}}$

avec probabilité $1 - α$ . Le réel $z 1 - α / 2$ est le quantile de la loi normale centrée réduite. Par exemple, au niveau de risque $\alpha = 5 \%$ , on trouve dans les tables $z 1 - α / 2 = 1,96$ et l'erreur est majorée par $1,96 \sigma_g/\sqrt{N}$ . Cette méthode permet donc de quantifier l'erreur commise, à condition d'estimer $σ g$ par sa contre-partie empirique

$\hat{\sigma}_g = \sqrt{S^2_{g(X)}}.$

On voit ainsi que l'erreur est de l'ordre de $N - 1 / 2$ : par exemple, multiplier la taille de l'échantillon par 100 permet de diviser par 10 l'erreur d'estimation.

Il est à noter qu'en pratique, $σ g$ n'est pas connu et doit être estimé ; comme précisé plus haut, on peut utiliser sa contre-partie empirique. Diverses méthodes, dites techniques de réduction de la variance, permettent d'améliorer la précision — ou de diminuer le temps de calcul — en remplaçant $g (X)$ par une autre variable aléatoire. Ces techniques rentrent en général dans l'une des classes suivantes : l'échantillonnage préférentiel, les variables de contrôle, la variable antithétique, la stratification et le conditionnement.

Exemples

Résolution du Problème du voyageur de commerce

La résolution du problème du voyageur de commerce est difficile, du fait de la complexité du problème, l'emploi de méthodes d'optimisation probabilistes peut s'avérer efficace pour obtenir une approximation de la meilleure solution, en un temps plus court que pour des méthodes déterministes.

Détermination de la valeur de π (pi)

Cette méthode est proche de l'expérience de l'aiguille de Buffon.

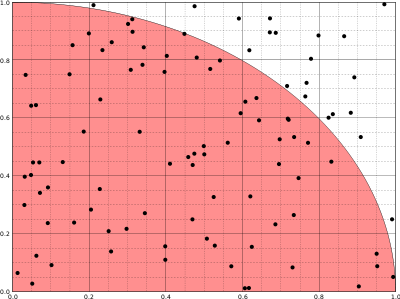
Soit un point $M$ de coordonnées $(x, y)$ , où $0 < x < 1$ et $0 < y < 1$ . On tire aléatoirement les valeurs de $x$ et $y$ . Le point $M$ appartient au disque de centre $(0,0)$ de rayon 1 si et seulement si $\scriptstyle x^2+y^2 \leq 1$ . La probabilité que le point $M$ appartienne au disque est ^π⁄₄.

En faisant le rapport du nombre de points dans le disque au nombre de tirages, on obtient une approximation du nombre ^π⁄₄ si le nombre de tirages est grand.

représentation du calcul de la valeur de pi par rapport du nombre de points aléatoires étant contenus dans un quart de cercle, l'ensemble des possibles étant un carré de côté R

Détermination de la superficie d'un lac

Cet exemple est un classique en vulgarisation de la méthode de Monte-Carlo. Soit une zone rectangulaire ou carrée dont les côtés sont de longueur connue. Au sein de cette aire se trouve un lac dont la superficie est inconnue. Grâce aux mesures des côtés de la zone, on connaît l'aire du rectangle. Pour trouver l'aire du lac, on demande à une armée de tirer X coups de canon de manière aléatoire sur cette zone. On compte ensuite le nombre N de boulets qui sont restés sur le terrain ; on peut ainsi déterminer le nombre de boulets qui sont tombés dans le lac : X-N. Il suffit ensuite d'établir un rapport entre les valeurs :

$\frac{\mathrm{superficie}_{~\mathrm{terrain}}}{\mathrm{superficie}_{~\mathrm{lac}}} = \frac{X}{X-N}$

$\Longrightarrow \qquad \mathrm{superficie}_{~\mathrm{lac}} = \frac{(X-N)}{X} \ \times \ \mathrm{superficie}_{~\mathrm{terrain}}$

Par exemple, si le terrain fait 1 000 m², que l'armée tire 500 boulets et que 100 projectiles sont tombés dans le lac, alors une estimation de la superficie du plan d'eau est de : 100*1000/500 = 200 m².

Estimation de la surface du lac grâce à des tirs d'artillerie aléatoires

La qualité de l'estimation s'améliore en augmentant le nombre de tirs et en s'assurant que les artilleurs ne visent pas toujours le même endroit mais couvrent bien la zone. Cette dernière remarque est à mettre en parallèle avec la qualité du générateur aléatoire qui est primordiale pour avoir de bons résultats dans la méthode de Monte-Carlo. Un générateur biaisé est comme un canon qui tire toujours au même endroit : les informations qu'il apporte sont réduites.

Application au modèle d'Ising

Article détaillé : Modèle d'Ising.

Estimation de la valeur d'un coup au go

Aux échecs, il est facile de mesurer la valeur d'une position, et donc d'un coup y menant, en comptant le nombre de pièces sur l'échiquier, en les pondérant (1 point par pion, 5 par tour...), et en ajustant la valeur trouvée par les libertés, les protections des pièces... Cela n'est pas possible au go. On a alors recours à une analyse de Monte-Carlo : on joue "au hasard" un grand nombre de parties, et on comptabilise la proportion que l'on en gagne. Cette estimation statistique peut s'affiner en biaisant le hasard de façon à éviter les coups stupides. Voir l'article dédié.

Estimation de la valeur d'un coup aux échecs

Parfois, pour savoir si un coup hasardeux doit être fait (échange de pièces par exemple), lorsqu'on manque d'information, ou pour choisir entre plusieurs coups menant tous à des pertes de matériel, il est possible de lancer plusieurs parties rapides au hasard, pour savoir quelle est la moins mauvaise ou la meilleure des solutions.

Notes et références

↑ Nicholas Metropolis, « The Beginning of the Monte Carlo Method », dans Los Alamos Science, n^o 15, 1987, p. 125-130 [texte intégral]
↑ Nicholas Metropolis et Stanislas Ulam, « The Monte Carlo Method », dans Journal of the American Statistical Association, vol. 44, n^o 247, septembre 1949, p. 335-341 [texte intégral] .

Voir aussi

Bibliographie

(fr) Introduction to Monte Carlo Algorithm Werner Krauth - CNRS, Laboratoire de Physique Statistique, École Normale Supérieure
(en) Michael Mascagni, Advanced Monte Carlo Methods I & II, Cours du ETH de Zurich (2005/2006). [PDF] Notes de cours. On pourra également consulter la page de présentation du cours, qui contient de nombreuses références disponibles au format en pdf.
Simon Léger, Monte Carlo pour les nuls, 2006 [PDF] [lire en ligne]
Une explication de la méthode de Monte-Carlo par le physicien Pierre Auger

Liens externes

(en) Un exemple de simulation Monte-Carlo clair et didactique L'exemple se base sur la fabrication d'une pièce mécanique à partir de ses composants.

Portail des probabilités et des statistiques
Portail de la physique
Portail de la finance

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Méthode de Monte-Carlo de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Methode de Monte-Carlo — Méthode de Monte Carlo Pour les articles homonymes, voir Monte Carlo (homonymie). On appelle méthode de Monte Carlo toute méthode visant à calculer une valeur numérique, et utilisant des procédés aléatoires, c est à dire des techniques… … Wikipédia en Français
Méthode De Monte-Carlo — Pour les articles homonymes, voir Monte Carlo (homonymie). On appelle méthode de Monte Carlo toute méthode visant à calculer une valeur numérique, et utilisant des procédés aléatoires, c est à dire des techniques probabilistes. Le nom de ces… … Wikipédia en Français
Méthode de Monte Carlo — Pour les articles homonymes, voir Monte Carlo (homonymie). On appelle méthode de Monte Carlo toute méthode visant à calculer une valeur numérique, et utilisant des procédés aléatoires, c est à dire des techniques probabilistes. Le nom de ces… … Wikipédia en Français
Méthode de monte-carlo — Pour les articles homonymes, voir Monte Carlo (homonymie). On appelle méthode de Monte Carlo toute méthode visant à calculer une valeur numérique, et utilisant des procédés aléatoires, c est à dire des techniques probabilistes. Le nom de ces… … Wikipédia en Français
Méthode cinétique Monte Carlo — Méthode de Monte Carlo cinétique La méthode de Monte Carlo cinétique, kinetic Monte Carlo (KMC) en anglais, est une méthode de Monte Carlo de simulation informatique permettant de simuler des processus se produisant à des taux connus. En cela… … Wikipédia en Français
méthode de Monte Carlo — Monte Karlo metodas statusas T sritis automatika atitikmenys: angl. Monte Carlo method vok. Monte Carlo Methode, f rus. метод Монте Карло, m pranc. méthode de Monte Carlo, f … Automatikos terminų žodynas
méthode de Monte-Carlo — Monte Karlo metodas statusas T sritis Standartizacija ir metrologija apibrėžtis Apytikslis kai kurių uždavinių sprendimo metodas, pagrįstas atsitiktinių dydžių verčių modeliavimu ir ieškomųjų dydžių verčių statistiniu įvertinimu. atitikmenys:… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
méthode de Monte-Carlo — Monte Karlo metodas statusas T sritis fizika atitikmenys: angl. Monte Carlo method vok. Monte Carlo Verfahren, n rus. метод Монте Карло, m pranc. méthode de Monte Carlo, f … Fizikos terminų žodynas
Methode de Monte-Carlo cinetique — Méthode de Monte Carlo cinétique La méthode de Monte Carlo cinétique, kinetic Monte Carlo (KMC) en anglais, est une méthode de Monte Carlo de simulation informatique permettant de simuler des processus se produisant à des taux connus. En cela… … Wikipédia en Français
Méthode De Monte-Carlo Cinétique — La méthode de Monte Carlo cinétique, kinetic Monte Carlo (KMC) en anglais, est une méthode de Monte Carlo de simulation informatique permettant de simuler des processus se produisant à des taux connus. En cela elle permet de simuler exactement le … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Méthode de Monte-Carlo

Sommaire

Théorie

Exemples