Ménisque divergent

Pour les articles homonymes, voir Lentille.

Une lentille

Une lentille est un élément, homogène, isotrope, transparent, traditionnellement en verre, dont au moins l’une des faces n’est pas plane et destiné à faire converger ou diverger la lumière.

Son utilisation implique que son indice de réfraction soit différent de celui du milieu dans lequel elle est plongée (air, huile, eau…). Les lentilles sont souvent réalisées en verre ou en matériau organique et possèdent la plupart du temps un axe de symétrie confondu avec l’axe optique.

Il existe aussi des lentilles qui agissent sur d’autres types d’onde électromagnétique, au moyen d’un champ électrique et/ou d’un champ magnétique.

Histoire

Les premières traces d’utilisation d’une lentille proviennent de la Grèce antique. Aristophane y fait notamment référence dans sa pièce Les Nuées écrite en 423 av. J.-C. en évoquant un verre à feu (une lentille convexe utilisée pour produire du feu en focalisant les rayons solaires).

Les écrits de Pline l'Ancien (23-79) montrent également qu’un tel dispositif était connu dans l’Empire romain. Ils mentionnent ce qui peut être interprété comme la première utilisation d’une lentille pour corriger la vue en décrivant l’utilisation que fait Néron d’une émeraude de forme convexe lors des spectacles de gladiateurs (probablement pour corriger une myopie). Sénèque le Jeune (3 av. J.-C. - 65) décrit l’effet grossissant d’un globe en verre rempli d’eau.

Le mathématicien arabe Alhazen (965-1038), a écrit le premier traité d’optique qui décrit comment le cristallin forme une image sur la rétine.

Les lentilles n’ont cependant pas été utilisées par le grand public avant la généralisation des lunettes de vue, probablement inventées en Italie dans les années 1280.

Principe

Propagation, réfraction

Dans un milieu transparent, homogène et isotrope, les ondes lumineuses se propagent en ligne droite. On définit l’indice de réfraction du milieu par le rapport

n = c/v,

où v est la vitesse de la lumière dans le milieu, et c la célérité de la lumière dans le vide. La vitesse v de la lumière est forcément inférieure à c, et l’indice de réfraction n — qui est une caractéristique propre du milieu (la lentille, par exemple) considéré — est donc toujours supérieur à 1. Lorsque l’onde lumineuse rencontre un dioptre (surface séparant deux milieux homogènes d’indices différents), la lumière est réfractée, c’est-à-dire déviée, en suivant les lois de Snell-Descartes. Cette déviation ne s’observe qu’à la condition que la lentille se trouve dans un milieu d’indice différent. Par ailleurs, on observe que la vitesse de propagation de la lumière dans l’air est sensiblement égale à celle dans le vide ( notée c).

Un schéma d’optique est toujours réalisé en considérant un sens donné de propagation de la lumière : du fait du principe de retour inverse de la lumière, l’ensemble du schéma est renversé si on considère le sens de propagation opposé.

Explication ondulatoire

Lentille plan convexe convergente

Lentille plan concave divergente

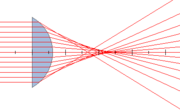
Si on considère une onde plane (les surfaces d’onde — ou surfaces équiphases — sont des plans perpendiculaires à la direction de propagation, c’est-à-dire que la direction de propagation est la même partout) qui arrive sur une lentille plan convexe perpendiculairement à sa face d’entrée, la partie de l’onde au bord de la lentille traversera moins de verre que celle au centre de la lentille : la surface équiphase va ainsi se déformer et devenir courbe. Si la lentille permet de la transformer en une onde parfaitement sphérique, elle convergera vers un point source situé derrière la lentille.

Le schéma ci-contre Lentille plan convexe convergente montre une telle lentille. Les traits rouges représentent les rayons lumineux, qui sont les directions de propagation de l’énergie lumineuse : dans le cas d’une onde plane, ces rayons sont parallèles entre eux. Ces rayons sont perpendiculaires à la face d’entrée de la lentille (les surfaces d’onde sont donc parallèles à cette face d’entrée) et ne sont pas déviés à sa traversée. Par contre, ils sont déviés lors de la traversée de la face de sortie, et convergent en aval de la lentille vers un point appelé point focal image.

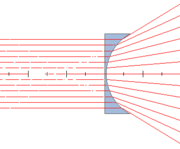
Dans le cas de la lentille divergente (schéma Lentille plan concave divergente), la partie de l’onde au centre de la lentille traverse moins de verre que celle aux bords. L’onde en sortie est déformée en une onde sphérique qui semble provenir d’un point source situé en amont de la lentille. On peut de nouveau effectuer des constructions à partir des rayons lumineux, qui suivent les lois de Snell-Descartes : le point focal image se trouve en amont de la lentille.

Définitions

Lentilles convergentes et divergentes

Selon la forme de ses faces d’entrée et de sortie, une lentille sera convergente ou divergente.

• Une lentille convergente transforme un faisceau de lumière parallèle (onde plane) en un faisceau qui converge vers un point situé en aval de la lentille.
• Une lentille divergente transforme un faisceau de lumière parallèle (onde plane) en un faisceau divergent qui semble provenir d’un point situé en amont de la lentille.

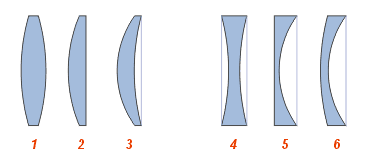Lentilles convergentes
1 - lentille biconvexe
2 - lentille plan-convexe
3 - ménisque convergent
Lentilles divergentes
4 - lentille biconcave
5 - lentille plan-concave
6 - ménisque divergent

On distingue six types de lentilles :

• les lentilles convergentes :
  • lentille biconvexe : les deux dioptres sont sphériques, les centres des sphères sont situés chacun d’un côté du plan de la lentille ;
  • lentille plan-convexe : un des dioptres est sphérique, l’autre est plan ;
  • ménisque convergent : les deux dioptres sont sphériques, les centres des sphères sont situés du même côté du plan de la lentille ;
• les lentilles divergentes :
  • lentille biconcave : les deux dioptres sont sphériques, les centres des sphères sont situés chacun d’un côté du plan de la lentille ;
  • lentille plan-concave : un des dioptres est sphérique, l’autre est plan ;
  • ménisque divergent : les deux dioptres sont sphériques, les centres des sphères sont situés du même côté du plan de la lentille.

² Le symbole en double flèche est utilisé dans le cas des lentilles minces, qui permet de simplifier les constructions grâce à certaines approximations lorsque l’on respecte les conditions de Gauss, c’est-à-dire lorsque les rayons qui frappent la lentille frappent à proximité du centre optique de la lentille et que leur direction est proche de l’axe optique.

Lentilles minces ou épaisses

Une lentille mince est une lentille qui remplit les trois conditions suivantes :

• l’épaisseur de la lentille est petite devant le rayon de la première face,
• l’épaisseur de la lentille est petite devant le rayon de la deuxième face,
• l’épaisseur de la lentille est plus petite que la valeur absolue de la différence entre le rayon de la première face et le rayon de la deuxième face.

Les lentilles épaisses n’ont pas les mêmes propriétés (aussi simples) que les lentilles minces.

Lentilles cylindriques

Les lentilles cylindriques sont donc des cylindres au sens large (forme obtenue en faisant translater une courbe selon une génératrice). Les dioptres sont eux-mêmes des cylindres.

Pour les rayons se propageant dans un plan contenant une génératrice, elles se comportent comme une vitre, le rayon n’est pas dévié. Pour les rayons se propageant dans un plan perpendiculaire aux génératrices, elles se comportent comme une lentille classique à symétrie axiale.

Elles sont principalement utilisées dans deux applications :

• à but pédagogique : vues dans l’axe des génératrices (« de profil »), elles sont similaires à une lentille classique vue en coupe ; cette forme permet de les placer de manière stable sur une table, ou de les placer sur un tableau avec des aimants, et de visualiser le trajet des rayons ;
• pour les anamorphoses : les rayons ne sont pas déviés de manière identique selon le plan de propagation, ce qui déforme l’image ; cette propriété est notamment utilisée en prise de vues anamorphique (CinemaScope), selon le principe de l’Hypergonar.

Lentille cylindrique biconcave

Lentille cylindrique plan-convexe

Lentille cylindrique biconcave utilisée pour une démonstration d’optique

Lentille cylindrique biconvexe utilisée pour une démonstration d’optique

Caractéristiques d’une lentille

On considère ici que l’on est dans les conditions de Gauss, et que le système est stigmatique : tous les rayons issus d’un point A convergent — après traversée de la lentille — en un point A′, ou semblent provenir d'un point A′ situé en amont de la lentille. A est appelé point objet, et A′ est le point image de A.

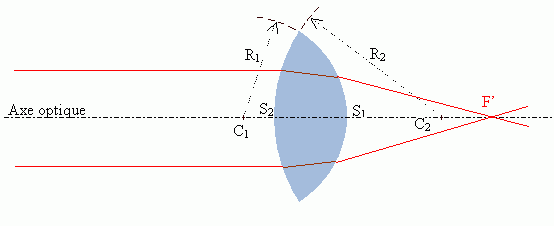Lentille convergente

Lentille convergente

Lentille divergente

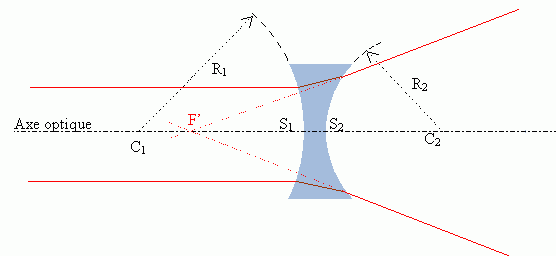Lentille divergente

Un système optique est un ensemble de milieux transparents et homogènes ou réflecteurs, séparés par des dioptres. Un système optique centré possède une symétrie de révolution autour d’un axe appelé axe optique. Une lentille seule possède donc un tel axe. On appelle centre optique le point de cet axe situé au milieu de la lentille.

Foyers objet et image

• On appelle foyer image F′ l’image d’un objet situé à l’infini : c’est donc le point où focalisent des rayons qui se propagent parallèlement à l’axe optique.
• On appelle foyer objet F le point dont l’image est située à l’infini : les rayons issus de ce point se propagent — après traversée de la lentille — parallèlement à l’axe optique.

Le plan perpendiculaire à l’axe optique et passant par F′ est appelé plan focal image, et ses points sont des foyers image secondaires.

Distances focales

En optique, on utilise des distances algébriques, marquées par une barre au-dessus de la quantité considérée, le sens de propagation de la lumière étant par convention le sens positif. On discerne deux distances focales :

ƒ′ = SF′

et

ƒ = SF,

où S est le centre optique de la lentille.

La distance algébrique ƒ′ est positive si F′ est situé en aval de la lentille (lentille convergente) et négative si F′ est en amont de la lentille (lentille divergente).

La détermination expérimentale de la distance focale ƒ′ d'une lentille optique s’appelle la focométrie.

Espaces objet et image

On considère une onde lumineuse se propageant selon un sens donné. Le demi-espace situé en amont de la lentille par rapport à ce sens de propagation est appelé espace objet. Le demi-espace situé en aval de la lentille est appelé espace image.

Si A est un objet situé en aval de la lentille, A est un objet virtuel et S₂A est positif ; si A est un objet réel situé en amont de la lentille, cette distance est négative. Pour une image réelle A′ située en aval de la lentille, S₁A′ est positif, et pour une image virtuelle située en amont de la lentille, S₁A′ est négatif (pour une lentille divergente, en prenant les notations des images ci-dessus, il faut inverser S₁ et S₂).

Aberrations

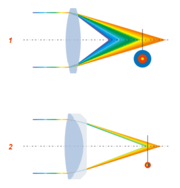
l’aberration chromatique obtenue (en 1) peut être corrigée par l’ajout d’une deuxième lentille (en 2)

Les lentilles optiques ne forment pas des images parfaites : l’image d’un point n’est généralement pas un point, mais une tache (astigmatisme). Ces aberrations affectent la qualité des images, mais peuvent cependant être minimisées par l’association de deux lentilles de verres optiques différents qui agissent en correction.

On classe les aberrations en 2 grandes familles :

• aberrations chromatiques : l’image se forme différemment selon la couleur de la lumière.
• aberrations géométriques, qui caractérisent les écarts à l’optique géométrique, écarts d’autant plus grands que l’on s’éloigne des conditions de Gauss, donc de l’axe optique.

Lentille électro-magnétique

Un champ magnétique ou électrique peut dévier des charges en mouvement.

Vision en mécanique classique

Si l’on assimile le trajet d’une charge à un rayon, on peut alors considérer que l’on a une lentille si des faisceaux de charges parallèles convergent en un point. Selon la déviation, on peut avoir une lentille convergente ou divergente.

Vision en mécanique quantique

Une charge ponctuelle, par exemple un électron, est une onde (voir l’article Dualité onde-corpuscule), et suit donc les règles de propagation classiques des ondes.

On peut appliquer le même formalisme que pour les lentilles optiques, et notamment la notion de plan focal, distance focale et d’aberration.

Les lentilles électromagnétiques sont utilisées par exemple pour focaliser les faisceaux d’électrons dans les microscopes électroniques.

Lentille liquide

Effets optiques de la rosée sur une prêle.

Les gouttes d’eau comme la rosée peuvent être une forme de lentille naturelle. De petites tailles, elles ont la forme d'une calotte sphérique. Plus grosses, elles se déforment sous leur propre poids. La valeur limite est de quelques millimètres pour l'eau. Elles sont ainsi employées dans certaines optiques des appareils photos des téléphones mobiles, permettant d'avoir une focale variable en déformant électriquement la lentille^[1].

Lentille gravitationnelle

Dans la théorie de la relativité générale, la masse courbe l’espace autour d’elle. La lumière est donc déviée par une masse importante, par exemple une étoile. Ce phénomène porte le nom de lentille gravitationnelle.

Voir aussi

Articles connexes

• Lentille de Fresnel
• Lentille de contact
• Superlentille
• Focométrie
• Aberrations des lentilles optiques
• Relation de conjugaison
• Verre correcteur
• Verre crown
• Verre flint

Réferences

Liens externes

• Une vidéo explicative sur les lentilles convergentes

• Portail de la physique