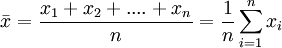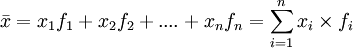Moyenne empirique

Moyenne empirique

Moyenne arithmétique

La moyenne arithmétique ou moyenne empirique d'une série statistique est la moyenne ordinaire, c'est-à-dire le rapport de la somme d’une distribution d’un caractère statistique quantitatif discret par le nombre de valeurs dans la distribution.

Sa formulation mathématique peut se faire comme suit :

\bar{x} = \frac{x_1 + x_2 + .. .. + x_n}{n} = {1 \over n} \sum_{i = 1}^n{x_i}

Pour une série statistique dont le nombre total d’occurrences est infini ou inconnu, mais dont les fréquences sont connues pour chaque valeur possible de la série, la formulation mathématique devient :

\bar{x} = x_1 f_1 + x_2 f_2 + .. .. + x_n f_n = \sum_{i = 1}^n{x_i \times f_i}

La moyenne arithmétique d'une distribution f d’une variable continue à valeur dans un intervalle scalaire fini [x0, x1] est la généralisation à la limite de la formule statistique discrète précédente :

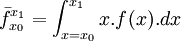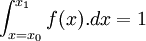\bar{f}_{x_0}^{x_1} = \int_{x = x_0}^{x_1}{x.f(x).dx}, où \int_{x = x_0}^{x_1}{f(x).dx} = 1.

Sa dimension n'est pas une fréquence, mais celle de la variable continue.

Si la distribution f est définie sur toutes les valeurs réelles de sa variable continue, la moyenne arithmétique de la distribution est :

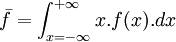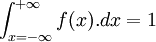\bar{f} = \int_{x = -\infin}^{+\infin}{x.f(x).dx}, où \int_{x = -\infin}^{+\infin}{f(x).dx} = 1.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Moyenne arithm%C3%A9tique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Moyenne empirique de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Moyenne Empirique — Moyenne arithmétique La moyenne arithmétique ou moyenne empirique d une série statistique est la moyenne ordinaire, c est à dire le rapport de la somme d’une distribution d’un caractère statistique quantitatif discret par le nombre de valeurs… …   Wikipédia en Français

  • Moyenne Arithmétique — La moyenne arithmétique ou moyenne empirique d une série statistique est la moyenne ordinaire, c est à dire le rapport de la somme d’une distribution d’un caractère statistique quantitatif discret par le nombre de valeurs dans la distribution. Sa …   Wikipédia en Français

  • Moyenne arithmetique — Moyenne arithmétique La moyenne arithmétique ou moyenne empirique d une série statistique est la moyenne ordinaire, c est à dire le rapport de la somme d’une distribution d’un caractère statistique quantitatif discret par le nombre de valeurs… …   Wikipédia en Français

  • Moyenne arithmétique — La moyenne arithmétique[1] ou moyenne empirique d une série statistique est la moyenne ordinaire, c est à dire le rapport de la somme d’une distribution d’un caractère statistique quantitatif discret par le nombre de valeurs dans la distribution …   Wikipédia en Français

  • Moyenne — Pour les articles homonymes, voir Valeur moyenne. La moyenne est une mesure statistique caractérisant les éléments d un ensemble de quantités : elle exprime la grandeur qu auraient chacun des membres de l ensemble s ils étaient tous… …   Wikipédia en Français

  • Fonction de répartition empirique — En Statistiques, une fonction de répartition empirique est une fonction de répartition qui attribue la probabilité 1/n à chacun des n nombres dans un échantillon. Soit un échantillon de variables iid à valeurs dans avec pour fonction de… …   Wikipédia en Français

  • Distribution empirique — Fonction de répartition empirique En Statistiques, une fonction de répartition empirique est une fonction de répartition qui attribue la probabilité 1/n à chacun des n nombres dans un échantillon. Soit un échantillon de variables iid à valeurs… …   Wikipédia en Français

  • Otite moyenne aigue — Otite moyenne aiguë L otite moyenne aiguë (OMA) est une maladie fréquente, liée à une infection du conduit auditif, le plus souvent d origine virale. Sommaire 1 Généralités 1.1 Épidémiologie 1.2 Bactériologie …   Wikipédia en Français

  • Otite moyenne aiguë — Pour consulter un article plus général, voir : otite. Otite moyenne aiguë Classification et ressources externes Otoscopie  …   Wikipédia en Français

  • Statistique mathematique — Statistique mathématique Pour les articles homonymes, voir Statistique. Les statistiques, dans le sens populaire du terme, traitent des populations. En statistique descriptive, on se contente de décrire un échantillon à partir de grandeurs comme… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”