- Mot sturmien
-
En mathématiques, un mot sturmien est un type de mot infini.
Sommaire
Définition 1
En combinatoire des mots, un mot infini est une suite infinie de symboles construite à partir d'un alphabet fini. Appelons toute sous-suite contiguë et finie un facteur de ce mot. Alors, un mot w est dit dit « sturmien » si, pour tout entier naturel n, w a exactement n + 1 facteurs différents de longueur n.
Remarquons qu'il doit y avoir 2 facteurs distincts de longueur 1, impliquant que l'alphabet utilisé est nécessairement un alphabet de 2 lettres. Sans perte de généralité, on peut les appeler 0 et 1.
Définition 2
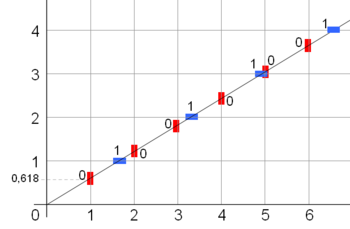Caractérisation d'un mot sturmien par une droite. Ici le mot de Fibonacci : pente φ-1 et passant par l'origine, où φ est le nombre d'or.
Une suite
sur {0,1} est un mot sturmien si et seulement s'il existe 2 nombres réels α et ρ, avec α irrationnel, tels que:Pour tout n.
Un mot sturmien peut être représenté par une discrétisation de la droite de pente α et d'ordonnée à l'origine ρ (voir illustration).
Puisque, pour tout entier k nous avons
, nous pouvons toujours prendre 0 < α < 1.Tous les mots sturmiens de même pente α partagent le même ensemble de facteurs.
Mot standard ou mot caractéristique
Le mot cα correspondant à ρ = 0 (droite passant par l'origine) est dit mot standard ou caractéristique de pente α. Donc, si 0 < α < 1, le mot caractéristique cα est constitué des écarts entre les termes de la suite de Beatty correspondant à l'irrationnel α.
Ce mot caractéristique peut aussi être obtenu de la façon suivante: Soit
![[0; d_1+1, d_2, \ldots, d_n, \ldots]](1/351f4694028742b995b00547a47f62fd.png)
le développement en fractions continues de α, et définissons :- s0 = 1
- s1 = 0
pour n > 0
(Souvenons-nous que le produit de deux mots est leur concaténation). Chaque mot dans la suite (sn)n > 0 est le préfixe des suivants, de telle sorte que la suite elle-même converge vers un mot infini qui est cα.
Un exemple célèbre de mot sturmien est le mot de Fibonacci ; sa pente vaut
, où φ est le nombre d'or.Histoire
Bien que l'étude des mots sturmiens remonte à Jean Bernouilli (en 1772), la première grande étude a été réalisée par Gustav Hedlund (de) et Marston Morse en 1940. Ils introduisirent le terme « sturmien » en l'honneur du mathématicien français Charles Sturm.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Sturmian word » (voir la liste des auteurs)
- (en) M. Lothaire, Algebraic Combinatorics on Words, Cambridge UK, Cambridge University Press, 2002 (ISBN 978-0-521-81220-7) (LCCN 2001037964) [lire en ligne], « Sturmian Words »
Wikimedia Foundation. 2010.
