- Séquence du lapin
-
Mot de Fibonacci
Un Mot de Fibonacci est une suite spécifique de lettres ou symboles pris dans un alphabet quelconque de deux lettres. Les mots de Fibonacci sont à l'opération de concaténation ce que les nombres de Fibonacci sont à l'addition.
Sommaire
Definition
A partir de l'alphabet {0;1}, Posons S1 = "1" and S2 = "0". alors le mot de Fibonacci Sn = Sn − 1Sn − 2 (La concaténation des deux précédents termes).
Le mot infini de Fibonacci est la limite
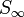 .
.Le mot de Fibonacci est baptisé par analogie avec la suite de Fibonacci, en substituant l'addition par la concaténation.
Les mots de Fibonacci successifs sont :
S1 1
S2 0
S3 01
S4 010
S5 01001
S6 01001010
S7 0100101001001
S8 010010100100101001010
...
Le mot infini de Fibonacci commence donc par : 010010100100101001010010010100100101001010010010100101... Cette suite infinie est la suite A003849 de l’OEIS.
On trouve dans la littérature également le terme "suite du Lapin", identique au mot de Fibonacci en inversant "0" et "1". La suite du Lapin commence donc par 101101011...
Propriétés
Expression analytique
La nieme lettre du mot de Fibonacci est
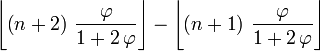 où
où est le Nombre d'or et
est le Nombre d'or et 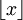 est la fonction partie entière (suite A003849 de l’OEIS).
est la fonction partie entière (suite A003849 de l’OEIS).Règle de substitution ou morphisme
Les mots de Fibonacci peuvent être définis via un morphisme (ou substitution).
Partant d'un mot de fibonacci Sn, on obtient le mot Sn + 1 en:
- remplaçant la lettre "1" par "0"
- remplaçant la lettre "0" par "01"
Que l'on peut aussi écrire:
Sn + 1 = σ(Sn) avec σ le morphisme défini par:
- σ(1) = 0 et
- σ(0) = 01
et, pour le mot infini de Fibonacci,
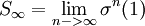 .
.On dit aussi que le mot infini de Fibonacci est le point fixe du morphisme σ car
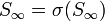 . Ce morphisme est appelé "Morphisme de Fibonacci".
. Ce morphisme est appelé "Morphisme de Fibonacci".Mot de Fibonacci et suite de Fibonacci
Mot de Fibonacci et Suite de Fibonacci sont étroitement liés. Chaque mot de Fibonacci étant la concaténation des deux précédents et partant de "1", puis "0", alors la longueur du mot de Fibonacci Sn vaut le nombre de Fibonacci Fn.
On écrit: | Sn | = Fn
Sn long.= Fn 1 1 0 1 01 2 010 3 01001 5 01001010 8 0100101001001 13 010010100100101001010 21 De même, on montre que:
- le nombre de "0" vaut Fn − 1
- le nombre de "1" vaut Fn − 2
Diverses propriétés
- Le mot infini de Fibonacci n'est pas périodique. Il n'est pas, non plus, ultimement périodique.
- Les deux dernières lettres d'un mot de Fibonacci sont alternativement "01" et "10"
- En supprimant les deux dernières lettres d'un mot de Fibonacci, on obtient un palindrome.
- En juxtaposant le complément binaire des deux dernières lettres d'un mot de Fibonacci au début de ce mot, on obtient un palindrome. Ainsi 01S6 = 0101001010 est un palindrome.
- Dans le mot infini de Fibonacci, le ratio nbre de lettres/nombre de "0" tend vers φ, le nombre d'or. De même que le ratio nombre de "0"/nombre de "1".
- Le mot de Fibonacci est "équilibré": Soit deux facteurs de même longueur pris n’importe où dans le mot de Fibonacci, la différence entre le nombre de "0" de l’un et le nombre de "0" de l’autre ne dépasse jamais la valeur 1. Nota: tout mot sturmien est équilibré.
- On ne peut trouver dans un mot de Fibonacci le facteur ("sous-mot") "11" ni "000".
- Dans le mot infini de Fibonacci, le nombre de facteurs (sous-mots) distincts de longueur k est k+1. Le mot infini de Fibonacci est donc un mot sturmien. Ainsi, les facteurs distincts de longueur 3 sont au nombre de 4: "001", "010", "100" et "101". Etant non-périodique, ce mot est alors de dit de "complexité minimale".
- Chaque facteur du mot infini de Fibonacci y apparait une infinité de fois.
- Si un mot est facteur du mot infini de Fibonacci, alors son inverse l'est aussi.
- La concaténation de deux mots de Fibonacci successifs est "presque commutative". Ainsi, Sn + 1 = SnSn − 1 et Sn − 1Sn diffèrent seulement sur les deux dernières lettres. Exemple: S8 = S7S6 = (0100101001001)(01001010) et S6S7 = (01001010)(0100101001001).
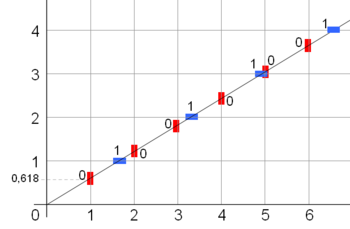
- Le mot infini de Fibonacci est le mot sturmien de pente 1 / φ2 avec φ, le nombre d'or
- Par conséquent, le mot infini de Fibonacci peut aussi se caractériser par la suite des intersections d'une droite de pente φ ou φ − 1 (φ = nombre d'or), avec les droites de coordonnées entières. Voir figure plus haut.
- Le nombre 0,010010100..., dont les décimales sont contruites à partir du mot infini de Fibonacci, est transcendant.
- Les lettres "1" se situent aux positions données par les valeurs successives de la suite Upper Wythoff (suite A001950 de l’OEIS) :
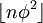
- Les lettres "0" se situent aux positions données par les valeurs successives de la suite Lower Wythoff (suite A000201 de l’OEIS) :
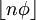
- Le mot de Fibonacci admet des répétitions de 3 sous-mots (cubes), comme "010", mais pas de répétitions de 4 sous-mots. On montre que le mot de Fibonacci admet au plus 2 + φ = 3,618 répétitions. C'est le plus faible index (ou "exposant critique") parmi les mots sturmiens.
- En théorie de la complexité, le mot de Fibonacci est souvent cité comme le "pire cas" pour un algorithme de recherche de répétitions dans une chaine de caractères.
Fractale du mot de Fibonacci
La fractale du mot de Fibonacci se construit itérativement en appliquant au mot de Fibonacci la règle OEDR (Odd-Even Drawing Rule). Pour chaque lettre en position k:
- tracer un segment
- et si "0" alors faire quart de tour:
- à droite si k est pair
- à gauche si k est impair
Pour un mot de Fibonacci de longueur Fn, une courbe de Fn segments est ainsi associée. Selon la valeur de n, la courbe se présente sous trois aspects différents: F3k, F3k + 1. et F3k + 2 (Voir figure ci-contre). Cette courbe a été étudiée pour ses propriétés.[1].
Voir aussi
References
Bibliographie
- Combinatorics on Words (Cambridge Mathematical Library). par M.Lothaire. ISBN - 978-0521599245
- Automatic Sequences par Jean-Paul Allouche and Jeffrey Shallit Cambridge University Press 2003
Articles connexes
Liens externes
- Une présentation détaillée et accessible, sur le site de Ron Knott
- Une introduction
- Mot infini de Fibonacci et morphismes itérés (article)
- Le mot de Fibonacci : suite A003849 de l’OEIS
- la "suite du Lapin" sur Mathworld
- [vidéo] Mot de Fibonacci sur YouTube.
- Portail des mathématiques
Catégorie : Suite d'entiers
Wikimedia Foundation. 2010.

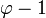 avec
avec 
