Angles alterne-interne
- Angles alterne-interne
-
Angles alternes-internes
En géométrie, deux droites coupées par une sécante forment des angles dont les sommets sont aux points d'intersection.
Définition
Deux angles formés par deux droites coupées par une sécante sont dits angles alternes-internes si :
- ils sont situés de part et d'autre de la sécante ;
- ils sont situés à l'intérieur des deux droites ;
- ils ne sont pas adjacents.
oui mais pas toujours
Droites quelconques
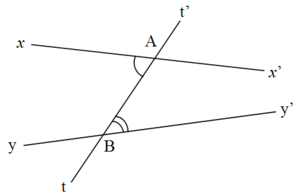
Les droites (xx') et (yy') sont coupées respectivement en A et en B par la sécante (tt').
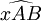 et
et 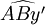 sont des angles alternes-internes.
sont des angles alternes-internes.
Droites parallèles
- Propriété
- Si deux droites parallèles sont coupées par une sécante, alors ces droites forment des angles alternes-internes égaux.
- Réciproquement, si deux droites coupées par une sécante forment des angles alternes-internes égaux, alors ces deux droites sont parallèles.
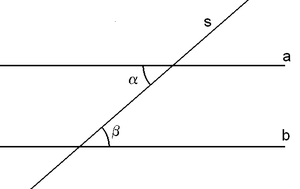
Sur la figure ci-dessus, les droites a et b sont parallèles et s est une sécante à ces deux droites.
α et β sont des "Angles égaux"
Voir aussi
 Portail de la géométrie
Portail de la géométrie
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Angles alterne-interne de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Angles Alterne-interne — Angles alternes internes En géométrie, deux droites coupées par une sécante forment des angles dont les sommets sont aux points d intersection. Sommaire 1 Définition 2 Droites quelconques 3 Droites parallèles … Wikipédia en Français
interne — [ ɛ̃tɛrn ] adj. et n. • 1560; « ce qui est à l intérieur » XIVe; lat. internus I ♦ Adj. 1 ♦ Qui est situé en dedans, est tourné vers l intérieur. ⇒ intérieur. Parois, parties internes. ♢ Math. Angles internes, opposés aux angles externes dans la… … Encyclopédie Universelle
interné — interne [ ɛ̃tɛrn ] adj. et n. • 1560; « ce qui est à l intérieur » XIVe; lat. internus I ♦ Adj. 1 ♦ Qui est situé en dedans, est tourné vers l intérieur. ⇒ intérieur. Parois, parties internes. ♢ Math. Angles internes, opposés aux angles externes… … Encyclopédie Universelle
CORMOPHYTES — Chez les Végétaux eucaryotes, on distingue par leur morphologie deux grands groupes, les Thallophytes, dont l’appareil végétatif est un thalle , tel celui des Algues ou des Champignons [cf. THALLE], et les Cormophytes (ou Archégoniates), dont… … Encyclopédie Universelle
Icosaedre — Icosaèdre Icosaèdre Type Polyèdre régulier Faces Triangle Éléments : · Faces · Arêtes · Sommets · Caractéristique 20 30 12 2 Faces par sommet 5 Sommets par face … Wikipédia en Français
Icosaèdre — Type Polyèdre régulier Faces Triangle Éléments : · Faces · Arêtes · Sommets · Caractéristique … Wikipédia en Français
Icosaédre — Icosaèdre Icosaèdre Type Polyèdre régulier Faces Triangle Éléments : · Faces · Arêtes · Sommets · Caractéristique 20 30 12 2 Faces par sommet 5 Sommets par face … Wikipédia en Français
Isocaèdre — Icosaèdre Icosaèdre Type Polyèdre régulier Faces Triangle Éléments : · Faces · Arêtes · Sommets · Caractéristique 20 30 12 2 Faces par sommet 5 Sommets par face … Wikipédia en Français
Réseau (groupe) — Réseau (géométrie) Pour les articles homonymes, voir Réseau. Un réseau est un ensemble discret de points qui emplissent un e … Wikipédia en Français
Réseau (géométrie) — Pour les articles homonymes, voir Réseau. En mathématiques, un réseau d un espace euclidien est un maillage correspondant à la figure de gauche … Wikipédia en Français
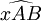 et
et 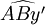 sont des angles alternes-internes.
sont des angles alternes-internes.

