- La Bissectrice
-
Bissectrice
En mathématiques, de façon informelle, une bissectrice est un demi-droite qui coupe un angle en deux parties égales. Cette notion peut être généralisée en nommant ainsi la droite qui se superpose à la demi-droite.
Sommaire
Définition
La bissectrice d'un secteur angulaire[1] le partage en deux secteurs angulaires superposables. C'est une demi-droite issue du sommet du secteur angulaire.
Proposition : l'axe de symétrie d'un secteur angulaire porte la bissectrice de ce secteur angulaire.
DémonstrationSi A, B et I sont trois points non alignés, on note B' le symétrique de B par rapport à la droite (AI).
- Comme A est sur l'axe de symétrie, AB = AB'. Le triangle BAB' est donc isocèle de sommet A
- par construction, (AI) est un (l')axe de symétrie du triangle.
- La symétrie axiale préserve les angles : ∠BAI = ∠IAB'. [AI) est donc la bissectrice de l'angle en A
D'un coup de compas, on peut toujours faire apparaître un triangle isocèle dans un secteur angulaire. L'axe de symétrie du triangle isocèle est aussi axe de symétrie pour le secteur angulaire. CQFDRemarque : Il peut être commode de décider d'appeler bissectrice tout l'axe et pas seulement la demi-droite contenue dans le secteur angulaire.
Théorème de la bissectrice
Théorème de la bissectrice — Tout point de la bissectrice d'un angle est à égale distance des côtés de cet angle.
Démonstration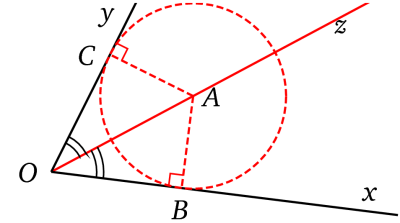 Démonstration du théorème de la bissectrice
Démonstration du théorème de la bissectriceOn note
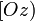 la bissectrice de l'angle
la bissectrice de l'angle 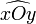 .
. 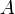 est un point de
est un point de 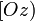 . Soient
. Soient 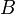 et
et 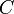 les projetés orthogonaux de
les projetés orthogonaux de 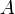 respectivement sur
respectivement sur 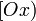 et sur
et sur 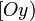 .
.- On sait que la distance de A à
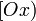 est AB ; de même la distance de A à
est AB ; de même la distance de A à 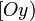 est
est 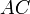 .
.
- par hypothèse,
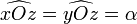 .
.
- Les relations trigonométriques dans les triangles rectangles OAC et OAB donnent :
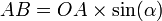 et
et 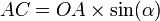 donc
donc 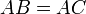 . CQFD
. CQFD
Si on revient à l'idée de bissectrice - axe de symétrie, donc de bissectrice - droite, on peut énoncer un
Théorème de la bissectrice (bis) — La bissectrice (droite) d'un angle est l'ensemble des points à égale distance des côtés de cet angle.
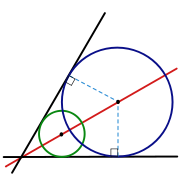
Corollaire : La bissectrice [Oz) d'un angle xOy est le lieu des centres des cercles tangents aux côtés [Ox) et [Oy) de cet angle.
Preuve du corollaire- Soit M un point de la bissectrice. On construit le point H sur le côté [Ox) tel que la droite (MH) est perpendiculaire à la demi-droite [Ox). On construit de même le point H' sur le côté [Oy). D'après le théorème, MH = MH', donc H et H' sont sur un même cercle C de centre M. De plus [Ox) est perpendiculaire au rayon [MH] donc [Ox) est tangente au cercle C. De même [Oy) est tangente au cercle C.
- Réciproquement, on suppose que C est un cercle de centre M, tangent à [Ox) en un point K et tangent à [Oy) en un point L. Comme (MK) est perpendiculaire à [Ox), MK est la distance de M à [Ox). De même ML est la distance de M à[Oy). Par hypothèse MK=ML donc M est sur la bissectrice de xOy d'après le théorème (bis). CQFD
Applications :- Construction au compas de la bissectrice
- Les bissectrices d'un triangle se rencontrent au centre du cercle inscrit.
Construction géométrique
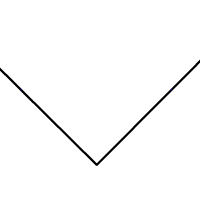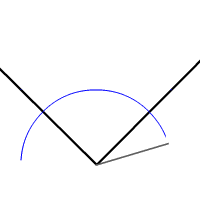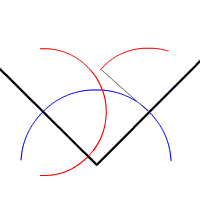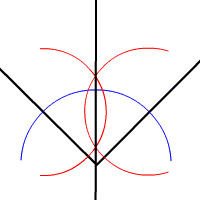 Animation montrant les étapes de la construction
Animation montrant les étapes de la construction
Comme conséquence du théorème de la bissectrice, voici une méthode de construction à la règle et au compas de la bissectrice d'un angle.
- Pointer le compas au sommet de l'angle et tracer un premier arc de cercle. Marquer les points d'intersection de cet arc avec les deux côtés de l'angle.
- Pointer successivement le compas aux points d'intersection tracer deux arcs de cercle de même rayon (en gardant le même écartement du compas entre les deux opérations). Marquer le point d'intersection de ces deux arcs.
- Relier le sommet de l'angle et le point d'intersection des deux derniers cercles et vous avez tracé la bissectrice de l'angle.
Il vous faut un compas, un crayon gris bien taillé, et une feuille.
Bissectrices de deux droites sécantes
Les bissectrices d'un couple de droites sécantes sont par définition les bissectrices des quatre secteurs angulaires définis par les deux droites. Il y a donc stricto sensu quatre bissectrices pour deux droites, si on s'en tient à la première définition de bissectrice. Au cours de la preuve du théorème suivant on montre que ces quatre bissectrices sont portées par deux droites qu'on appellera bissectrices des droites sécantes.
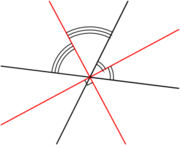
Théorème — Les bissectrices d'un couple de droites sécantes sont perpendiculaires.
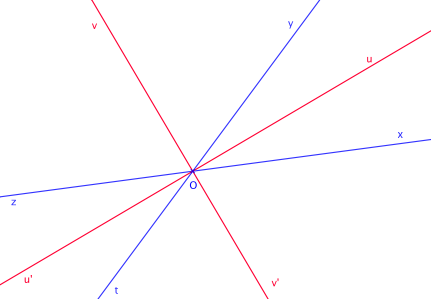
DémonstrationNotons (zx) et (ty) les deux droites. Elles se coupent en un point O. On appelle :
- [Ou) la bissectrice de xOy
- [Ou') la bissectrice de zOt
- [Ov) la bissectrice de yOz
- [Ov') la bissectrice de tOx
- Les angles xOy et zOt sont opposés par le sommet. Ils sont donc égaux. Les angles xOu = 1/2 xOy et zOu'=1/2 zOt sont donc aussi égaux. Comme [Ox) et [Oz) sont portées par une même droite il en va de même de [Ou) et [Ou') (on a aussi utilisé le fait que [Ou') est tracée dans le secteur zOt). Il en va de même pour les autres couples de bissectrices.
- Par hypothèse, les angles zOy et yOx sont supplémentaires : zOy + yOx = 180°. Donc uOv = uOy + yOv = 1/2 xOy + 1/2 yOz = 1/2 (xOy + yOz) = 180°/2 = 90°. CQFD
Bissectrices comme axes de symétrie de D u D'.— Si u et v sont deux vecteurs unitaires dirigeant respectivement D et D', alors u+v et u-v dirigent les axes de symétrie de la réunion D u D' (dessiner les losanges).
On obtient ainsi la notion de bissectrice de deux droites affines sécantes sans passer par le point de vue naïf des angles géométriques. Le produit scalaire (u+v).(u-v) est nul comme u et v sont unitaires : les deux bissectrices sont orthogonales.
Bissectrices de deux droites et faisceaux harmoniques[2] —
- Si D et D' sont deux droites sécantes et
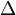 ,
, 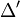 sont leurs bissectrices alors D, D',
sont leurs bissectrices alors D, D', 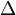 et
et 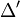 forment un faisceau harmonique.
forment un faisceau harmonique.
- Si D, D',
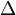 et
et 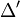 forment un faisceau harmonique et si
forment un faisceau harmonique et si 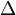 et
et 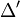 sont perpendiculaire alors
sont perpendiculaire alors 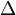 et
et 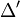 sont les bissectrices de D et D'
sont les bissectrices de D et D'
Bissectrices d'un triangle
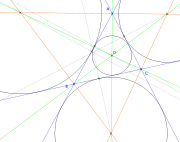
Cercles inscrit et exinscrits à un triangle — Dans un triangle,
- les bissectrices intérieures sont concourantes, leur point commun étant le centre du cercle inscrit dans le triangle. Ce cercle est tangent aux trois côtés du triangle.
- Deux bissectrices extérieures concourent avec la bissectrice intérieure restante. On obtient ainsi les centres des trois cercles exinscrits au triangle.
Démonstration — Pour le premier point du théorème, le point d'intersection de deux bissectrices intérieures est à égale distance des trois côtés du triangle. Il est donc aussi sur la troisième bissectrice intérieure. Un cercle centré au point de concours et tangent à un côté sera tangent aux deux autres (appliquer le corollaire du théorème de la bissectrice (bis))
Théorème — Dans un triangle MAB avec I sur [AB], la droite (MI) est la bissectrice de l'angle en M si et seulement si MA/MB = IA/IB.
On obtient la preuve de ce point à partir de la construction du conjugué harmonique (double Thalès).
Applications :
- On utilise extensivement la caractérisation précédente de la bissectrice dans l'étude du problème d'Apollonius : lieu des M tels que MA/MB = k.
- Avec cette caractérisation de la bissectrice, on retrouve aisément la bissectrice d'un angle MFN, où M et N sont deux points sur une ellipse de foyer F et de directrice D.[3]
Voir aussi
Notes et références
- Portail de la géométrie
Catégories : Angle | Ligne droite | Théorème de mathématiques
Wikimedia Foundation. 2010.