Cercles exinscrits

Cercles inscrit et exinscrits d'un triangle

Étant donnés trois points non alignés A, B et C du plan, il existe quatre cercles tangents aux trois droites (AB), (AC) et (BC). Ce sont le cercle inscrit (pour celui qui est intérieur au triangle) et les cercles exinscrits du triangle ABC.

Bissectrices

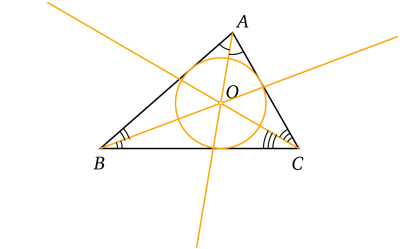Bissectrices et cercle inscrit d'un triangle.

Les trois bissectrices d'un triangle sont concourantes. Leur intersection est le centre d'un cercle tangent au trois côtés du triangle : c'est le cercle inscrit dans le triangle.

Démonstration :

Rappel: la bissectrice d'un angle est l'ensemble des points équidistants des deux droites.

Si K est la l'intersection de deux bissectrices (par ex celle de l'angle de sommet A et celle de l'angle de sommet B):

on a distance (K, (AB))= distance(K,(AC)) puisque K appartient à la première bissectrice et distance (K,(BA)) = distance (K,(BC)) puisque K appartient à la deuxième bissectrice

On a donc distance (K,(CA))= distance (K,(CB)) et K appartient bien à la troisième bissectrice et comme il est équidistant des trois droites, on peut donc bien tracer un cercle inscrit dont il est le centre

Si on considère les trois côtés du triangle en tant que droites, on dispose en tout de 6 bissectrices : 2 bissectrices pour chaque couple de droites. Par chacun des sommets du triangle, passe une bissectrice intérieure (qui rencontre le côté opposé du triangle) et une bissectrice extérieure (qui est l'autre bissectrice).

Deux bissectrices extérieures associées à deux sommets et la bissectrice intérieure associée au troisième sommet sont concourantes. (La démonstration est analogue à celle ci-dessus). Leur point d'intersection est à égale distance des trois côtés du triangle (en tant que droites). Il permet donc de tracer un cercle tangent aux trois côtés du triangle : un cercle exinscrit au triangle.

Les 3 cercles exinscrits d'un triangle.

Cercle inscrit

Notation : dans cet article nous notons $A$ , $B$ et $C$ les trois sommets du triangle, $a$ la longueur du côté $B C$ , $b$ la longueur du côté $A C$ et $c$ la longueur du côté $A B$ .

Enfin $O$ désigne le centre du cercle inscrit et $O A$ , $O B$ et $O C$ les trois centres des cercles exinscrits (voir figure ci-dessous).

Propriété: Les trois bissectrices intérieures d'un triangle sont concourantes.

Démonstration

La bissectrice d'un angle est l'axe de symétrie de cet angle. Chaque point de la bissectrice est donc à égale distance des deux côtés de l'angle.

De ce fait, le point d'intersection $O$ de deux bissectrices est à égale distance des côtés des deux angles correspondants, donc des trois droites $(A B)$ , $(A C)$ et $(B C)$ .

Ce point est donc à égale distance des deux côtés du troisième angle, donc sur la troisième bissectrice : les trois bissectrices sont concourantes.

Propriété: Il existe un et un seul cercle intérieur au triangle et tangent à la fois à ses trois côtés. Ce cercle de centre 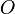$O \,$ est appelé « cercle inscrit » dans le triangle.

Démonstration

D'après la propriété précédente des bissectrices, on peut tracer, à l'intérieur du triangle, un cercle de centre $O$ qui est tangent aux trois droites $(A B)$ , $(A C)$ et $(B C)$ : c'est le cercle inscrit dans le triangle. Il existe trois autres cercles ayant la même propriété (mais situés à l'extérieur du triangle) qu'on appelle cercles exinscrits du triangle.

Le cercle inscrit à un triangle est le plus grand cercle que peut contenir ce triangle. Son centre est le barycentre des points $(A, a)$ $(B, b)$ $(C, c)$ . Son rayon est égal à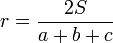

$r=\frac{2S}{a+b+c}$

où $S$ désigne la surface du triangle.

Point de Gergonne

Notons respectivement $T A$ , $T B$ et $T C$ les points de contact du cercle inscrit avec les côtés $[B C]$ , $[A C]$ et $[A B]$ . Alors les droites $(A T A)$ , $(B T B)$ et $(C T C)$ sont concourantes : leur point d'intersection s'appelle le point de Gergonne du triangle. D'ailleurs, le triangle $T A T B T C$ s'appelle le triangle de Gergonne du triangle $A B C$ .

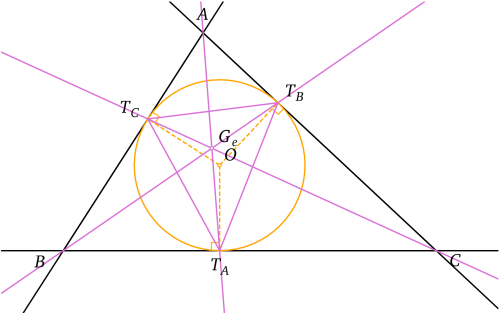Point de Gergonne d'un triangle.

Cercles exinscrits

Il y a donc trois cercles exinscrits : chacun est tangent à un unique côté du triangle (considéré comme un segment). Nous nommons $C A$ le cercle exinscrit touchant le côté $[C B]$ , $C B$ le cercle exinscrit touchant le côté $[A C]$ et $C C$ le cercle exinscrit touchant le côté $[A B]$ .

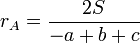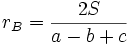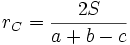
Les rayons des cercles exinscrits sont respectivement $r_A = \frac{2S}{-a+b+c}$ , $r_B = \frac{2S}{a-b+c}$ et $r_C = \frac{2S}{a+b-c}$

Leurs centres sont barycentres des points $(A, - a)$ $(B, b)$ $(C, c)$ pour le premier, $(A, a)$ $(B, - b)$ $(C, c)$ pour le second et $(A, a)$ $(B, b)$ $(C, - c)$ pour le troisième.

Point de Nagel

Notons $U A$ le point de contact de $C A$ avec $[C B]$ , $U B$ le point de contact de $C B$ avec $[A C]$ et $U C$ le point de contact de $C C$ avec $[A B]$ .

Alors les droites $(A U A)$ , $(B U B)$ et $(C U C)$ sont concourantes : leur point d'intersection s'appelle le point de Nagel du triangle. On appelle le triangle $U A U B U C$ triangle de Nagel du triangle $A B C$ .

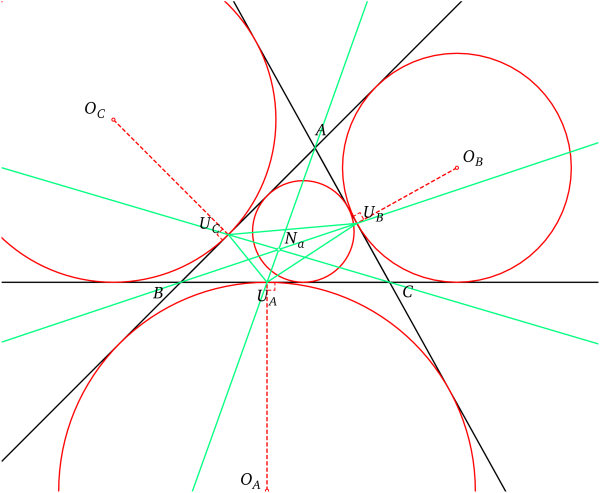Point de Nagel d'un triangle.

Point de Bevan

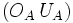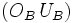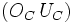Les droites $(O_A\,U_A)$ , $(O_B\,U_B)$ et $(O_C\,U_C)$ sont également concourantes : leur point d'intersection s'appelle le point de Bevan du triangle $A B C$ . D'ailleurs, le triangle 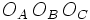$O_A\,O_B\,O_C$ s'appelle le triangle de Bevan de $A B C$ . Le point de Bevan est le centre du cercle circonscrit au triangle de Bevan.

Le triangle de Bevan et le triangle de Gergonne sont homothétiques.

Point et triangle de Bevan.

Point d'Apollonius

Il existe un unique cercle tangent simultanément aux trois cercles exinscrits et qui les contient (voir Problème des contacts); c'est le cercle d'Apollonius du triangle. De plus, si on note $V A$ , $V B$ et $V C$ les trois points de tangence alors les droites $(A V A)$ , $(B V B)$ et $(C V C)$ sont concourantes : leur point d'intersection s'appelle le point d'Apollonius du triangle.

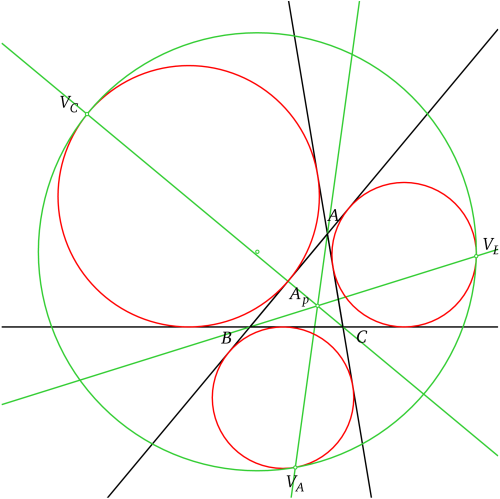Point d'Apollonius d'un triangle.

Théorème de Feuerbach

Les trois cercles exinscrits et le cercle inscrit sont tangents au cercle d'Euler du triangle. Les points de contact de ces cercles s'appellent les points de Feuerbach du triangle. Ce résultat constitue le théorème de Feuerbach.

Les trois points de tangence des cercles exinscrits forment le triangle de Feuerbach du triangle.

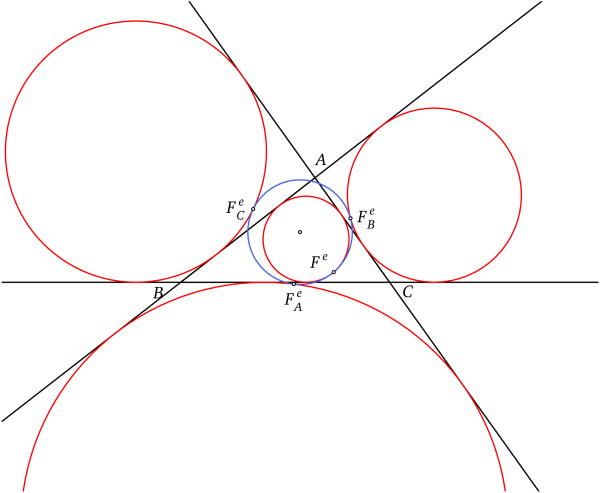Triangle de Feuerbach.

Portail de la géométrie

Ce document provient de « Cercles inscrit et exinscrits d%27un triangle ».

Catégories : Géométrie du triangle | Cercle et sphère

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Cercles exinscrits de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Cercles Exinscrits — Cercles inscrit et exinscrits d un triangle Étant donnés trois points non alignés A, B et C du plan, il existe quatre cercles tangents aux trois droites (AB), (AC) et (BC). Ce sont le cercle inscrit (pour celui qui est intérieur au triangle) et… … Wikipédia en Français
Cercles Inscrit Et Exinscrits D'un Triangle — Étant donnés trois points non alignés A, B et C du plan, il existe quatre cercles tangents aux trois droites (AB), (AC) et (BC). Ce sont le cercle inscrit (pour celui qui est intérieur au triangle) et les cercles exinscrits du triangle ABC.… … Wikipédia en Français
Cercles inscrit et exinscrits d'un triangle — Les 3 cercles exinscrits d un triangle et son cercle inscrit. Étant donnés trois points non alignés A, B et C du plan, il existe quatre cercles tangents aux trois droites (AB), (AC) et (BC). Ce sont le cercle inscrit (pour celui qui est intérieur … Wikipédia en Français
Points de Feuerbach — Cercles inscrit et exinscrits d un triangle Étant donnés trois points non alignés A, B et C du plan, il existe quatre cercles tangents aux trois droites (AB), (AC) et (BC). Ce sont le cercle inscrit (pour celui qui est intérieur au triangle) et… … Wikipédia en Français
Triangle — Pour les articles homonymes, voir Triangle (homonymie). Un triangle. En géométrie euclidienne, un trian … Wikipédia en Français
Bissectrice — La demi droite en rouge coupe l angle en deux parties égales : il s agit de la bissectrice de cet angle. En mathématiques, de façon informelle, une bissectrice est une demi droite qui coupe un angle en deux parties égales. Cette notion peut… … Wikipédia en Français
La Bissectrice — Bissectrice La demi droite en rouge coupe l angle en deux parties égales : il s agit de la bissectrice. En mathématiques, de façon informelle, une bissectrice est un demi droite qui coupe un angle en deux parties égales. Cette notion peut… … Wikipédia en Français
Théorème de la bissectrice — Bissectrice La demi droite en rouge coupe l angle en deux parties égales : il s agit de la bissectrice. En mathématiques, de façon informelle, une bissectrice est un demi droite qui coupe un angle en deux parties égales. Cette notion peut… … Wikipédia en Français
Cercle Des Neuf Points — Cercle d Euler Cercle et droite d Euler d un triangle En géométrie, le cercle d Euler d un triangle (aussi appelé cercle des neuf points, cercle de Feuerbach, cercle de Terquem, cercle médian) est l unique cercle passant par les neuf points… … Wikipédia en Français
Cercle Des Neufs Points — Cercle d Euler Cercle et droite d Euler d un triangle En géométrie, le cercle d Euler d un triangle (aussi appelé cercle des neuf points, cercle de Feuerbach, cercle de Terquem, cercle médian) est l unique cercle passant par les neuf points… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Cercles exinscrits

Cercles inscrit et exinscrits d'un triangle

Sommaire

Bissectrices