Isometrie partielle

Isometrie partielle

Isométrie partielle

En analyse fonctionnelle, une isométrie partielle est une application linéaire entre deux espaces de Hilbert dont la restriction au complément orthogonal de son noyau est une isométrie.
Ce complément orthogonal du noyau est appelé le sous-ensemble initial et son image est appelée sous-ensemble final.

Exemples

  1. Tout opérateur unitaire sur un espace de Hilbert est une isométrie partielle dont les espaces initiaux et finaux sont l'espace de Hilbert considéré.
  2. Sur l'espace de Hilbert de dimension C2, l'application linéaire représentée par la matrice 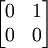\begin{bmatrix}0 & 1 \\ 0 & 0 \end{bmatrix} est une isométrie partielle ayant pour espace initial 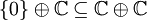\{0\} \oplus \mathbb{C} \subseteq \mathbb{C} \oplus \mathbb{C} et d'espace final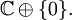 \mathbb{C} \oplus \{0\}.

Autre définition

Si U est une isométrie définie sur sous-espace fermé H1 d'un espace de Hilbert H, alors il existe une unique extension W de U sur tout H qui soit une isométrie partielle. Cette extension est définie en la prolongeant par 0 sur le complément orthogonal de H1.
On appelle ainsi parfois isométrie partielle une isométrie définie sur un sous-espace fermé d'un Hilbert.

Caractérisation

Les isométries partielles sont aussi caractérisées par le fait que soit W W* ou soit W* W soit une projection. Si cela se produit, W W* et W* W sont toutes 2 des projections. Cela permet de définir une isométrie partielle pour des C*-algèbres de la manière suivante:

Si A est une C*-algèbre, W ∈ A est une isométrie partielle si et seulement si W W* ou W* West une projection (endomorphisme autoadjoint idempotent) dans A. Dans ce cas W W* et W* W sont des projections, et

  1. W*W est appelée projection initiale de W.
  2. W W* est appelée projection finale de W.

Quand A est algèbre d'opérateurs, l'image de ces projections sont respectivement des sous-espaces initiaux et finauxde W.

On peut aussi montrer que les isométries partielles sont caractérisées par l'équation:

W = WW * W.

2 projection, dont l'une est la projection initiale et l'autre la projection finale sont dites équivalentes.Il s'agit d'une relation d'équivalence et joue un rôle important en K-théorie pour les C*-algèbres, et dans la théorie des projections de Murray-von Neumann pour des Algèbre de von Neumann.

Ce document provient de « Isom%C3%A9trie partielle ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Isometrie partielle de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Isométrie Partielle — En analyse fonctionnelle, une isométrie partielle est une application linéaire entre deux espaces de Hilbert dont la restriction au complément orthogonal de son noyau est une isométrie. Ce complément orthogonal du noyau est appelé le sous… …   Wikipédia en Français

  • Isométrie partielle — En analyse fonctionnelle, une isométrie partielle est une application linéaire entre deux espaces de Hilbert dont la restriction au complément orthogonal de son noyau est une isométrie. Ce complément orthogonal du noyau est appelé le sous… …   Wikipédia en Français

  • Partielle Isometrie — Eine partielle Isometrie ist ein spezieller Typ von im mathematischen Teilgebiet der Funktionalanalysis untersuchten Operatoren. Dabei handelt es sich um Operatoren, die sich auf einem Teilraum wie eine Isometrie verhalten und sonst 0 sind, das… …   Deutsch Wikipedia

  • Decomposition en valeurs singulieres — Décomposition en valeurs singulières En mathématiques, le procédé d algèbre linéaire de décomposition en valeurs singulières (ou SVD, de l anglais : Singular Value Decomposition) d une matrice est un outil important de factorisation des… …   Wikipédia en Français

  • Décomposition En Valeurs Singulières — En mathématiques, le procédé d algèbre linéaire de décomposition en valeurs singulières (ou SVD, de l anglais : Singular Value Decomposition) d une matrice est un outil important de factorisation des matrices rectangulaires réelles ou… …   Wikipédia en Français

  • Décomposition en valeurs singulières — En mathématiques, le procédé d algèbre linéaire de décomposition en valeurs singulières (ou SVD, de l anglais : Singular Value Decomposition) d une matrice est un outil important de factorisation des matrices rectangulaires réelles ou… …   Wikipédia en Français

  • Dimensionsfunktion — Die hier vorgestellte Typklassifikation teilt die in der Mathematik untersuchten von Neumann Algebren in Klassen ein, die man Typ nennt. Diese auf Francis J. Murray und John von Neumann zurückgehende Klassifizierung beruht auf einer Analyse der… …   Deutsch Wikipedia

  • Diskrete von-Neumann-Algebra — Die hier vorgestellte Typklassifikation teilt die in der Mathematik untersuchten von Neumann Algebren in Klassen ein, die man Typ nennt. Diese auf Francis J. Murray und John von Neumann zurückgehende Klassifizierung beruht auf einer Analyse der… …   Deutsch Wikipedia

  • Echt unendliche von-Neumann-Algebra — Die hier vorgestellte Typklassifikation teilt die in der Mathematik untersuchten von Neumann Algebren in Klassen ein, die man Typ nennt. Diese auf Francis J. Murray und John von Neumann zurückgehende Klassifizierung beruht auf einer Analyse der… …   Deutsch Wikipedia

  • Endliche von-Neumann-Algebra — Die hier vorgestellte Typklassifikation teilt die in der Mathematik untersuchten von Neumann Algebren in Klassen ein, die man Typ nennt. Diese auf Francis J. Murray und John von Neumann zurückgehende Klassifizierung beruht auf einer Analyse der… …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”