Algèbre Enveloppante

Algèbre Enveloppante

Algèbre enveloppante

En mathématiques, on peut construire l'algèbre enveloppante U(L) d'une algèbre de Lie L. Il s'agit une algèbre associative unitaire qui permet de rendre compte de la plupart des propriétés de L.

Si A est une algèbre associative sur un corps K, on peut facilement la munir d'une structure d'algèbre de Lie, en posant [x,y]=xy-yx. On note l'algèbre de Lie ainsi obtenue AL.

La construction d'une algèbre enveloppante répond au problème réciproque : à partir d'une algèbre de Lie, on construit une algèbre associative dont le commutateur correspond au crochet dont on était parti.

Construction

Soit L une algèbre de Lie sur un corps K. Soit T(L) l'algèbre tensorielle de L. On construit U(L) à partir de T(L) en imposant les relations x\otimes y-y\otimes x=[x,y].

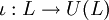Plus formellement, on note I l'idéal bilatère engendré par les x\otimes y-y\otimes x-[x,y]. U(L) est alors le quotient de T(L) par l'idéal I. L'injection canonique de L dans T(L) fournit alors un morphisme \iota:L\to U(L).

Propriété universelle

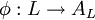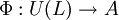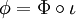On peut caractériser l'algèbre enveloppante de L par la propriété universelle suivante : U(L) est l'unique algèbre assocative telle que pour toute K-algèbre associative A et tout morphisme d'algèbre de Lie \phi : L\to A_L, il existe un unique morphisme d'algèbre associative \Phi:U(L)\to A tel que \phi=\Phi\circ \iota.

Autres propriétés

  • L'intérêt premier de la construction de l'algèbre enveloppante est que toute représentation d'une algèbre de Lie L peut être vue comme un module sur U(L). Formellement, il y a une équivalence de catégories entre les représentations de L et les U(L)-modules.
  • Le théorème de Poincaré-Birkhoff-Witt permet de mieux comprendre la structure de l'algèbre enveloppante. Un corollaire important de ce théorème est que l'application ι définie ci-dessus est injective.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Alg%C3%A8bre enveloppante ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Algèbre Enveloppante de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Algebre enveloppante — Algèbre enveloppante En mathématiques, on peut construire l algèbre enveloppante U(L) d une algèbre de Lie L. Il s agit une algèbre associative unitaire qui permet de rendre compte de la plupart des propriétés de L. Si A est une algèbre… …   Wikipédia en Français

  • Algèbre enveloppante — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, on peut construire l algèbre enveloppante d une algèbre de Lie . Il s agit une algèbre unitaire qui permet de rendre compte de la plupart des propriétés de …   Wikipédia en Français

  • Algebre de Lie — Algèbre de Lie En mathématiques, une algèbre de Lie, nommée en l honneur du mathématicien Sophus Lie, est un espace vectoriel (parfois même une algèbre) qui est munie d un crochet de Lie. Sommaire 1 Définitions, exemples et premières propriétés 1 …   Wikipédia en Français

  • Algèbre De Lie — En mathématiques, une algèbre de Lie, nommée en l honneur du mathématicien Sophus Lie, est un espace vectoriel (parfois même une algèbre) qui est munie d un crochet de Lie. Sommaire 1 Définitions, exemples et premières propriétés 1.1 Définition …   Wikipédia en Français

  • Algèbre de lie — En mathématiques, une algèbre de Lie, nommée en l honneur du mathématicien Sophus Lie, est un espace vectoriel (parfois même une algèbre) qui est munie d un crochet de Lie. Sommaire 1 Définitions, exemples et premières propriétés 1.1 Définition …   Wikipédia en Français

  • Algèbre de Lie — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, une algèbre de Lie, nommée en l honneur du mathématicien Sophus Lie, est un espace vectoriel qui est muni d un crochet de Lie, c est à dire d une loi de composition interne… …   Wikipédia en Français

  • Algèbre universelle — Pour les articles homonymes, voir Algèbre (homonymie). L algèbre universelle est la branche de l algèbre qui a pour but de traiter de manière générale et simultanée les différentes structures algébriques : groupes, monoïdes, anneaux, espaces …   Wikipédia en Français

  • Algèbre (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le mot « algèbre » vient de l arabe ’al ǧabr (« réduction »), désignant une technique de chirurgie des membres puis une technique de… …   Wikipédia en Français

  • Algèbre involutive — En mathématiques, une algèbre involutive est une algèbre munie d une isomorphisme sur son algèbre opposée, et donc le carré est l identité. Dans cet article, K désigne un anneau commutatif, et les algèbres sur un anneau commutatif sont supposées… …   Wikipédia en Français

  • Représentation d'algèbre de Lie — En mathématiques, une représentation d une algèbre de Lie est une façon d écrire cette algèbre comme une algèbre de matrices, ou plus généralement d endomorphismes d un espace vectoriel, avec le crochet de Lie donné par le commutateur. Sommaire 1 …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”