- Algorithme de tracé de cercle d'andres
-
Algorithme de tracé de cercle d'Andres
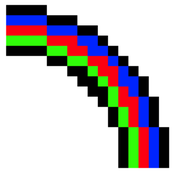
L’algorithme de tracé de cercle d'Andres permet, pour une complexité algorithmique très réduite, de tracer des cercles en image matricielle. Cet algorithme permet de paver entièrement le plan par des cercles concentriques, sans les trous que laisse par exemple l'algorithme de tracé d'arc de cercle de Bresenham.
Principe
Andres considère que les cercles discrets de rayon r et de centre (x0,y0) sont les ensembles des points vérifiant
(E) :
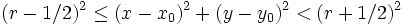
On procède par itération sur les points. Plaçons-nous dans un octant, par exemple celui juste au-dessus de l'Axe des abscisses, et supposons que le point P ait déjà été placé. On cherche alors à déterminer s'il faut choisir le point A, le point B ou le point C.
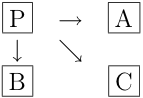
On montre alors que si P vérifie (E), alors seuls A, B ou C peuvent vérifier (E). De plus, A et B s'excluent mutuellement. Enfin, si ni A ni B ne vérifient (E), alors C vérifie (E).
On pose d = r2 + r − x2 − y2 − 1 et on montre que l'on doit choisir A si d > 2x et B si d < 2(r − y) .
Algorithme
Cet algorithme décrit le tracé d'un octant, les sept autres s'obtenant par symétrie.
x <- 0 y <- r d <- r - 1 Tant que y>=x TracerPixel(x, y) Si d >= 2x alors d <- d-2x-1 x <- x+1 Sinon Si d <= 2(r-y) alors d <- d+2y-1 y <- y-1 Sinon d <- d+2(y-x-1) y <- y-1 x <- x+1 Fin de tant que
Algorithme de tracé du cercle complet
x <- 0 y <- r d <- r - 1 Tant que y>=x tracerPixel( x+x_centre , y+y_centre ) tracerPixel( y+x_centre , x+y_centre ) tracerPixel( -x+x_centre , y+y_centre ) tracerPixel( -y+x_centre , x+y_centre ) tracerPixel( x+x_centre , -y+y_centre ) tracerPixel( y+x_centre , -x+y_centre ) tracerPixel( -x+x_centre , -y+y_centre ) tracerPixel( -y+x_centre , -x+y_centre ) Si d >= 2x alors d <- d-2x-1 x <- x+1 Sinon Si d <= 2(r-y) alors d <- d+2y-1 y <- y-1 Sinon d <- d+2(y-x-1) y <- y-1 x <- x+1 Fin de tant que
Pavage du plan par les cercles d'Andres concentriques
Pavage du plan par cercle concentriques
En traçant des cercles concentriques, on obtient bien un pavage complet du plan.
Ceci permet notamment de tourner des images avec une moindre déformation.
Portail de la géométrie
Portail de l’informatique
Catégories : Algorithme d'infographie | Cercle et sphère
Wikimedia Foundation. 2010.
