Algorithme de tracé d'arc de cercle de bresenham

Algorithme de tracé d'arc de cercle de bresenham

Algorithme de tracé d'arc de cercle de Bresenham

L’algorithme de tracé d'arc de cercle de Bresenham, ou algorithme de tracé d'arc de cercle par point milieu (midpoint en anglais) permet, pour une complexité algorithmique très réduite, de tracer des cercles en image matricielle.

Sommaire

Historique

Cet algorithme n'aurait pas été écrit par Jack E. Bresenham, mais inspiré de son travail sur le tracé de segments. Cet algorithme serait issu de travaux de Pitteway [1] et van Aken [2].

Explication de l'algorithme de base dans le premier octant

Un huitième suffit

Tout d'abord, on peut remarquer que sur une grille de pixels, il existe quatre axes de symétrie au cercle, deux suivant les axes de la matrice, et deux représentant les bissectrices du repère centré sur le cercle. Ainsi, ayant calculé un arc d'un secteur du repère délimité par les axes de symétrie, il suffit d'exploiter la symétrie pour positionner les sept autres pixels.

L'algorithme de base

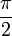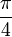Pour les raisons de symétrie expliquées précédemment, l'algorithme expliqué sera limité au deuxième octant (d'angle compris entre \frac{\pi}{2} et \frac{\pi}{4}) puis généralisé ensuite. L'algorithme partira donc du point le plus haut du cercle, et descendra jusqu'à la première bissectrice.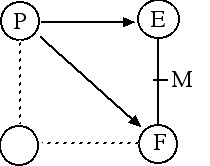

Schéma

Ce tracé procède par itération, chaque itération activant un pixel. Imaginons que nous sommes en un pixel P, et qu'il faut placer le pixel suivant. Puisque nous sommes dans le deuxième octant, ce pixel sera le point E ou le point F. La méthode de Bresenham consiste à évaluer si le cercle "idéal" d'équation x2 + y2 − R2 = 0 passe au-dessus ou en dessous du point M, milieu du segment EF pour activer respectivement le pixel E ou le pixel F.

Il faut donc calculer à chaque itération une variable m telle que 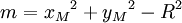m={x_M}^2+{y_M}^2-R^2. Alors :

  • m > 0 ⇒M au-dessus du cercle idéal ⇒ choix de F ⇒ incrémenter x, décrémenter y
  • m < 0 ⇒ M au-dessous du cercle idéal ⇒ choix de E ⇒ incrémenter x

Optimisation de l'algorithme

Pour optimiser l'algorithme, on calcule la variable m récursivement. On montre que 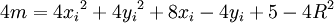4m=4{x_i}^2+4{y_i}^2+8x_i-4y_i+5-4R^2 (1)


démonstration

Plaçons-nous au point Pi de coordonnées sur la grille de pixel (xi;yi) et calculons la variable m.

On sait alors que M a pour coordonnées (xm = xi + 1;ym = yi − 0,5).

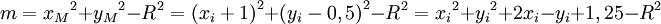Donc m={x_M}^2+{y_M}^2-R^2={(x_i+1)}^2+{(y_i-0,5)}^2-R^2={x_i}^2+{y_i}^2+2x_i-y_i+1,25-R^2.

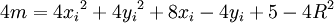Puisqu'on souhaite ne travailler qu'avec des nombres entiers, et puisque seul le signe de m nous intéresse, on multiplie l'équation par 4 et on obtient 4m=4{x_i}^2+4{y_i}^2+8x_i-4y_i+5-4R^2.


On va modifier la variable m en fonction du choix du pixel E ou du pixel F. On nommera mi l'ancienne valeur de m, et mi + 1 la nouvelle valeur de m.

  • On montre que si on choisit E, 4mi + 1 = 4mi + 8xi + 12 = 4mi + 8xi + 1 + 4.

Il faut donc incrémenter 4mi de 8xi + 1 + 4.


démonstration

Si on choisit E, alors (xi + 1 = xi + 1,yi + 1 = yi).

Or d'après l'équation (1),

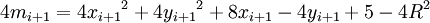4m_{i+1}=4{x_{i+1}}^2+4{y_{i+1}}^2+8x_{i+1}-4y_{i+1}+5-4R^2,

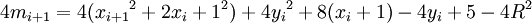
donc 4m_{i+1}=4({x_{i+1}}^2+2x_i+1^2)+4{y_i}^2+8(x_i+1)-4y_i+5-4R^2

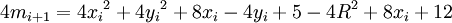d'où 4m_{i+1}=4{x_i}^2+4{y_i}^2+8x_i-4y_i+5-4R^2+8x_i+12.

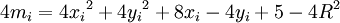En utilisant le fait que 4m_i=4{x_i}^2+4{y_i}^2+8x_i-4y_i+5-4R^2,

on obtient 4mi + 1 = 4mi + 8xi + 12 = 4mi + 8xi + 1 + 4.

  • On montre que si on choisit F, (xi + 1 = xi + 1,yi + 1 = yi + 1).

Il faut donc incrémenter 4mi de 8xi + 1 + 4 − 8yi + 1.


démonstration

Raisonnement analogue à celui où l'on choisit E

On en déduit donc le calcul itératif de m : mi + 1 = mi + 8xi + 1 + 4 − d avec d qui vaut 0 si on choisit E, et 8yi + 1 si on choisit F.

Pour amorcer le calcul itératif, on remarque que m0 = ( − 1)2 + (R − 0,5)2 − R2 donc 4m0 = 5 − 4R.

Algorithme optimisé

Algorithme de tracé d'un octant

procédure tracerOctant (entier rayon, entier x_centre, entier y_centre)
	déclarer entier x, y, m ;
	x ←0 ;
	y ← rayon ; 	//on se place en haut du cercle 
	m ←5-4*rayon ;		// initialisation
	Tant que x <= y 	// tant qu'on est dans le second octant
		tracerPixel( x+x_centre , y+y_centre ) ;
		si m > 0 alors	// choix du point F
			y ← y - 1 ;
			m ← m-8*y ;	// correspond au "d" des explications
		fin si ;
		x ← x+1 ;
		m ← m + 8*x+4 ;
	fin tant que ;
fin de procédure ;

La variable m représente le "4m" du paragraphe précédent, puisque seul le signe de 4m nous intéresse et qu'il est le même que celui de m.

Algorithme de tracé du cercle entier

procédure tracerOctant (entier rayon, entier x_centre, entier y_centre)
	déclarer entier x, y, m ;
	x ←0 ;
	y ← rayon ; 	// on se place en haut du cercle 
	m ←5-4*rayon ;		// initialisation
	Tant que x <= y 	// tant qu'on est dans le second octant
		tracerPixel( x+x_centre , y+y_centre ) ;
		tracerPixel( y+x_centre , x+y_centre ) ;
		tracerPixel( -x+x_centre , y+y_centre ) ;
		tracerPixel( -y+x_centre , x+y_centre ) ;
		tracerPixel( x+x_centre , -y+y_centre ) ;
		tracerPixel( y+x_centre , -x+y_centre ) ;
		tracerPixel( -x+x_centre , -y+y_centre ) ;
		tracerPixel( -y+x_centre , -x+y_centre ) ;
		si m > 0 alors	//choix du point F
			y ← y - 1 ;
			m ← m-8*y ;
		fin si ;
		x ← x+1 ;
		m ← m + 8*x+4 ;
	fin tant que ;
fin de procédure ;

On procède simplement par symétrie dans les différents octants.

Remarques sur la méthode de Bresenham

La faible complexité

On a vu précédemment que pour chaque pixel placé la complexité de calcul se réduisait à X additions, Y multiplications et Z comparaisons. L'utilisation de fonctions trigonométriques usuelles ou d'une racine carrée auraient nécessité un coût algorithmique considérable en comparaison.

Illustration des "trous"

Extensions

On peut également se servir du principe de cet algorithme pour tracer des couronnes et des ellipses.

Limites de la méthode

Si l'on trace des cercles concentriques de rayon de plus en plus grand, on remarque que l'on ne parvient pas à remplir tout le plan : il y a des "trous" . Ce défaut amène à utiliser d'autres méthodes, comme l'algorithme de tracé de cercle d'Andres.

Notes

  1. ↑ Pitteway, M.L.V., "Algorithm for Drawing Ellipses or Hyperbolae with a Digital Plotter", Computer J., 10(3) Novembre 1967, pp 282-289
  2. ↑ Van Aken, J.R., "An Efficient Ellipse Drawing Algorithm", CG&A, 4(9), Septembre 1984, pp 24-35
  • Portail de la géométrie Portail de la géométrie
  • Portail de l’informatique Portail de l’informatique
Ce document provient de « Algorithme de trac%C3%A9 d%27arc de cercle de Bresenham ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Algorithme de tracé d'arc de cercle de bresenham de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Algorithme De Tracé D'arc De Cercle De Bresenham — L’algorithme de tracé d arc de cercle de Bresenham, ou algorithme de tracé d arc de cercle par point milieu (midpoint en anglais) permet, pour une complexité algorithmique très réduite, de tracer des cercles en image matricielle. Sommaire 1… …   Wikipédia en Français

  • Algorithme de trace d'arc de cercle de Bresenham — Algorithme de tracé d arc de cercle de Bresenham L’algorithme de tracé d arc de cercle de Bresenham, ou algorithme de tracé d arc de cercle par point milieu (midpoint en anglais) permet, pour une complexité algorithmique très réduite, de tracer… …   Wikipédia en Français

  • Algorithme de tracé d'arc de cercle de Bresenham — L’algorithme de tracé d arc de cercle de Bresenham, ou algorithme de tracé d arc de cercle par point milieu (midpoint en anglais) permet, pour une complexité algorithmique très réduite, de tracer des cercles en image matricielle. Sommaire 1… …   Wikipédia en Français

  • Algorithme De Tracé De Cercle D'Andres — L’algorithme de tracé de cercle d Andres permet, pour une complexité algorithmique très réduite, de tracer des cercles en image matricielle. Cet algorithme permet de paver entièrement le plan par des cercles concentriques, sans les trous que… …   Wikipédia en Français

  • Algorithme de trace de cercle d'Andres — Algorithme de tracé de cercle d Andres L’algorithme de tracé de cercle d Andres permet, pour une complexité algorithmique très réduite, de tracer des cercles en image matricielle. Cet algorithme permet de paver entièrement le plan par des cercles …   Wikipédia en Français

  • Algorithme de tracé de cercle d'andres — L’algorithme de tracé de cercle d Andres permet, pour une complexité algorithmique très réduite, de tracer des cercles en image matricielle. Cet algorithme permet de paver entièrement le plan par des cercles concentriques, sans les trous que… …   Wikipédia en Français

  • Arc de cercle — Cercle Pour les articles homonymes, voir cercle (homonymie). Un cercle est une courbe plane fermée constituée des points situés à égale distance d un point nommé centre. La valeur de cette distance est appelée rayon du cercle. Celui ci étant… …   Wikipédia en Français

  • Algorithme de tracé de cercle d'Andres — L’algorithme de tracé de cercle d Andres permet, pour une complexité algorithmique très réduite, de tracer des cercles en image matricielle. Cet algorithme permet de paver entièrement le plan par des cercles concentriques, sans les trous que… …   Wikipédia en Français

  • Algorithme De Tracé De Segment De Bresenham — L’algorithme de tracé de segment de Bresenham est un algorithme développé par Bresenham en mai 1962, alors qu’il travaillait dans un laboratoire informatique d’IBM et cherchait à piloter un traceur attaché à une console texte. Cet algorithme a… …   Wikipédia en Français

  • Algorithme de trace de segment de Bresenham — Algorithme de tracé de segment de Bresenham L’algorithme de tracé de segment de Bresenham est un algorithme développé par Bresenham en mai 1962, alors qu’il travaillait dans un laboratoire informatique d’IBM et cherchait à piloter un traceur… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”