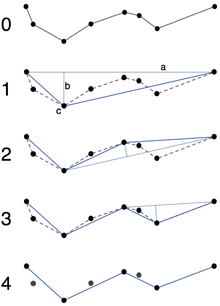
Algorithme de Douglas-Peuker

L’algorithme de Ramer-Douglas-Peuker sert à simplifier un polygone ou une polyligne par la suppression de nœud. Il est beaucoup utilisé en compression de données vectorielles et en généralisation cartographique.

Principe

Une polyligne (n nœuds) est simplifiable et remplacée par une ligne simple (deux nœuds) si la distance de son nœud le plus éloigné de la droite formée par les extrémités de la polyligne est inférieure à un seuil.

Algorithme

Réduction des points d'une courbe par l'algorithme de Ramer-Douglas-Peucker.

L'algorithme travaille de manière récursive par la méthode « diviser pour régner ».

À l'initialisation on sélectionne le premier et le dernier nœud (cas d'une polyligne), ou un nœud quelconque (cas d'un polygone). Ce sont les bornes.

À chaque étape on parcourt tous les nœuds entre les bornes et on sélectionne le nœud le plus éloigné du segment formé par les bornes :

1. s'il n'y a aucun nœud entre les bornes l'algorithme se termine,
2. si cette distance est inférieure à un certain seuil on supprime tous les nœuds entre les bornes,
3. si elle est supérieure la polyligne n'est pas directement simplifiable. On appelle de manière récursive l'algorithme sur deux sous-parties de la polyligne : de la première borne au nœud distant, et du nœud distant à la borne finale.

Pseudocode

function DouglasPeucker(PointList[], epsilon)
  // Trouve le point le plus éloigné du segment
  dmax = 0
  index = 0
  for i = 2 to (length(PointList) - 1)
    d = DistancePointSegment(PointList[i], Segment(PointList[1], PointList[end])) 
    if d > dmax
      index = i
      dmax = d
    end
  end
 
  // Si la distance dmax est supérieure au seuil, on simplifie
  if dmax >= epsilon
    // Appel récursif de la fonction
    recResults1[] = DouglasPeucker(PointList[1…index], epsilon)
    recResults2[] = DouglasPeucker(PointList[index…end], epsilon)
  
    // Construit la liste des résultats à partir des résultats partiels
    ResultList[] = {recResults1[1…end-1] recResults2[1…end]}

  else
    // Tous les points sont proches → renvoie un segment avec les extrémités
    ResultList[] = {PointList[1], PointList[end]}
  end
 
  // Renvoie le nouveau résultat
  return ResultList[]
end

Complexité

On remarquera que l'algorithme se finit forcément puisque dans le pire des cas la polyligne (ou le polygone) n'est pas simplifiable et chaque branche formée par la récursion s'achèvera lorsque les bornes ne seront pas séparées par un nœud (cas 1).

La complexité est en puisque dans le pire des cas aucune simplification n'est effectuée et chaque branche de la récursion se termine par le cas 1. À chaque étape le nombre de branches de récursion est multiplié par deux et tous les nœuds sont visités.

• Portail de l’algorithmique