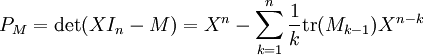- Algorithme de Faddeev
-
Algorithme de Faddeev-Leverrier
L' algorithme de Faddeev-Leverrier est une méthode permettant de calculer le polynôme caractéristique d'une matrice. Il porte le nom du mathématicien russe Dmitrii Konstantinovich Faddeev. Publié pour la première fois par Urbain Jean Joseph Le Verrier (1840), il fut re-découvert à de nombreuses reprises : Horst (1935), Souriau (1948), Frame (1949), Faddeev et Sorminskii (1949).
Présentation
Calculer le polynôme caractéristique d'une matrice carré M d'ordre n revêt une importance pratique fondamentale, puisque c'est un moyen d'accéder aux valeurs propres de M. Cependant, ce problème est hautement calculatoire, et l'algorithme naïf, qui consisterait à calculer directement le déterminant det(XIn − M) est extrêmement lourd sur le plan de la complexité algorithmique : il s'agit d'un déterminant, qui s'écrit comme somme de n! termes, où n désigne la taille de la matrice M.
L'algorithme de Faddeev s'inscrit dans une démarche d'efficacité. Partons de la matrice M, dont on cherche le polynôme caractéristique PM.
On définit par récurrence la suite finie de matrice
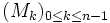 par :
par :-
- M0 = M
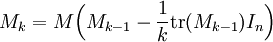 pour
pour 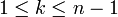
Alors on montre[1] que le polynôme caractéristique de M vaut :
Complexité de l'algorithme de Faddeev
Les coefficients du polynôme caractéristique s'expriment en termes de traces, de produits et de somme de matrices, ce qui les rend facilement calculables, tout du moins pour une machine. La complexité de l'algorithme de Faddeev est polynomiale, tandis que la complexité de l'algorithme naïf (calcul direct du déterminant de X In - M) est factorielle.
Notes
- ↑ Cf. par exemple The Theory of Matrices in Numerical Analysis (éd. Dover) par A. S. Householder.
- Portail des mathématiques
Catégorie : Matrice -
Wikimedia Foundation. 2010.