Algorithme De Remplissage Par Diffusion

L'algorithme de remplissage par diffusion est un algorithme classique en infographie qui change la couleur d'un ensemble connexe de pixels de même couleur délimités par des contours. Il est fréquemment utilisé par les programmes de manipulation d'images matricielles. Il trouve également son application dans certains jeux tels que le démineur, Puyo Puyo et Lumines afin de déterminer quels éléments du plateau de jeu sont à révéler.

Sommaire 1 Principe général 2 Formulation récursive 2.1 Variante 4-connexe 2.2 Variante 8-connexe 3 Algorithmes à pile explicite 3.1 Optimisations 3.1.1 En bouclant vers l'est et vers l'ouest 3.1.2 En balayant les lignes 4 Voir aussi 4.1 Liens externes

Principe général

L'algorithme de remplissage par diffusion prend 3 paramètres pour une image donnée : la position du pixel de départ (appelé aussi germe), la couleur ciblée (colcible) et la couleur de remplacement (colrep). L'algorithme recense tous les pixels de l'image qui sont connectés au germe par un chemin de la couleur ciblée et substitue à cette dernière la couleur de remplacement. Il y a plusieurs manière de structurer cet algorithme mais elles font toutes appel à une pile de manière implicite ou explicite pour effectuer le calcul.

Formulation récursive

La formulation récursive utilise une pile de manière implicite.

Variante 4-connexe

Si l'image est constituée de manière classique de pixels carrés ou rectangulaire, La variante 4-connexe considère les 4 voisins d'un pixel ayant en commun un bord avec ce dernier. La formulation de l'algorithme est la suivante :

 remplissage4(pixel, colcible, colrep) 
 début
   si couleur(pixel) = colcible 
   alors
      couleur(pixel)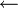  colrep
      remplissage4(pixel au nord,   colcible, colrep)
      remplissage4(pixel au sud,    colcible, colrep)
      remplissage4(pixel à l'est,   colcible, colrep)
      remplissage4(pixel à l'ouest, colcible, colrep)
   finsi
 fin

Variante 8-connexe

Cette variante considère les 8 cases voisines du pixel dans l'image : les cases adjacentes et diagonales. La formulation est la suivante :

 remplissage8(pixel, colcible, colrep) 
 début
   si couleur(pixel) = colcible 
   alors
      couleur(pixel)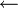  colrep
      remplissage8(pixel N,  colcible, colrep)
      remplissage8(pixel S,  colcible, colrep)
      remplissage8(pixel E,  colcible, colrep)
      remplissage8(pixel O,  colcible, colrep)
      remplissage8(pixel NE, colcible, colrep)
      remplissage8(pixel NO, colcible, colrep)
      remplissage8(pixel SE, colcible, colrep)
      remplissage8(pixel SO, colcible, colrep)
   finsi
 fin 

Cette variation de l'algorithme peut franchir certains contours qui sont des barrières pour la variante 4-connexe. Aussi, il convient de choisir l'algorithme à appliquer en fonction du résultat voulu.

Algorithmes à pile explicite

La formulation recursive précédente, si elle possède l'avantage d'être intuitive par sa formulation, est souvent inemployée en pratique, en particulier dans des environnements d'exécution où la pile d'appel des fonctions est fortement contrainte ou réduite. Il convient alors de créer sa propre pile dans laquelle seront stockés les pixels à explorer. L'algorithme pour la variante 4-connexe est alors le suivant :

 remplissage4(pixel, colcible, colrep)
 début
   Soit P une pile vide
   si couleur(pixel) 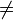 colcible alors sortir finsi
   Empiler pixel sur P
   Tant que P non vide
   faire
     Dépiler n de P
     couleur(n) 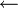 colrep
     si couleur(n nord) = colcible alors Empiler n nord sur P finsi
     si couleur(n sud)  = colcible alors Empiler n sud  sur P finsi
     si couleur(n est)  = colcible alors Empiler n est  sur P finsi
     si couleur(n ouest)= colcible alors Empiler n ouest sur P finsi
   fintantque
 fin

Optimisations

En bouclant vers l'est et vers l'ouest

La plupart des implémentations utilisent une boucle se propageant à la fois vers "l'est" et vers "l'ouest" afin d'alléger la gestion de la pile. L'algorithme utilisé est alors :

 remplissage4(pixel, colcible, colrep)
 début
   Soit P une pile vide
   si couleur(pixel) 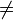 colcible alors sortir finsi
   Empiler pixel sur P
   Tant que P non vide
   faire
     Dépiler n de P
     si  couleur(n) = colcible
     alors 
       w 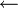 n 
       e 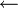 n
       Déplacer w vers l'ouest jusqu'à ce que couleur(w) 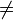 colcible
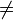       Déplacer e vers l'est   jusqu'à ce que couleur(e)  colcible
       Pour tout pixel p entre w et e
       Faire
         couleur(p) 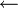 colrep
         si couleur(p nord) = colcible alors Empiler p nord sur P finsi
         si couleur(p sud ) = colcible alors Empiler p sud  sur P finsi
       finpour
     finsi
   fintantque
 fin 

En balayant les lignes

L'algorithme peut être accéléré en remplissant directement des lignes. Au lieu d'empiler chaque nouveau pixel potentiel, il suffit d'inspecter les lignes suivantes et précédentes qui seront coloriées lors d'une future passe. Les coordonnées des extremités du segment à colorier sont alors empilées. Dans la plupart des cas, cette variante de l'algorithme s'avère plus rapide que la version se basant sur les pixels.

Voir aussi

Liens externes

• (fr) Cours d'algorithmique pour l'infographie
• (en) Code source de l'algorithme en Java, C et OCaml
• (en) Exemples de réalisation de l'algorithme dans ses version récursives, non-récursives, dans ses versions classique et à base de balayage de lignes.