- Calcul de la racine cubique d'un nombre
-
Calcul de la racine n-ième d'un nombre
La racine n-ième (ou, rarement, racine énième) d'un nombre réel positif A, se notant
![\sqrt[n]{A}](/pictures/frwiki/51/3078170f7aedde3f7a90dcfb305c6533.png) , est la solution positive de l'équation xn = A avec
, est la solution positive de l'équation xn = A avec 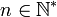 .
.Pour un entier n, il y a n solutions complexes distinctes pour cette équation si A > 0, mais une seule est réelle et positive.
Il s'agit en fait de calculer :
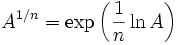 .
.
(ce qui découle de la relation exprimant un nombre strictement positif élevé à une puissance quelconque :
si a > 0 et
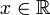 alors
alors 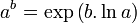 )
)Il existe une suite mathématique qui converge très rapidement, et permet de trouver
![\sqrt[n]{A}](/pictures/frwiki/51/3078170f7aedde3f7a90dcfb305c6533.png) :
:- Soit x0 un nombre de départ ;
- Calculer la suite récurrente
![x_{k+1} = \frac{1}{n} \left[{(n-1)x_k +\frac{A}{x_k^{n-1}}}\right]](/pictures/frwiki/54/609d6ace4927f7ffd374fa504c34e617.png) jusqu'à obtenir la précision voulue.
jusqu'à obtenir la précision voulue.
Par exemple, pour calculer la racine carrée, on remplace n par 2 :
Pour de grands n cependant, la méthode est bien moins efficace, puisqu'elle demande le calcul de
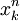 à chaque itération de la suite.
à chaque itération de la suite.Explication à partir de la méthode de Newton
- Soit x0 un nombre de départ et soit f(x) = xn − A une fonction de
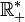 dans
dans  ;
; - Calculer la suite récurrente
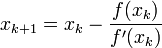 jusqu'à atteindre la précision voulue.
jusqu'à atteindre la précision voulue.
En effet, la recherche d'une racine nième peut être ramenée à la recherche du zéro de la fonction f(x) = xn − A, dont la dérivée est
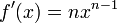 et la règle d'itération :
et la règle d'itération :Nombres négatifs, parité de n
Si A est négatif, on distingue deux cas :
- Si n est pair.
L'équation xn = A n'admet aucune solution réelle.
Néanmoins, il existe des solutions complexes
- Si n est impaire.
Calculer
![\sqrt[n]{A}](/pictures/frwiki/51/3078170f7aedde3f7a90dcfb305c6533.png) revient à calculer
revient à calculer ![-\sqrt[n]{-A}](/pictures/frwiki/55/7691717175aa4734ad7abb8aaf4883c1.png) .
.− A étant bien sur positif, les méthodes décrites précédemment s'appliquent.
Liens internes
- Portail des mathématiques
Catégories : Analyse réelle | Racine nième
Wikimedia Foundation. 2010.

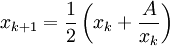
![x_{k+1} = x_k - \frac{f(x_k)}{f'(x_k)} = x_k - \frac{x_k^n - A}{n x_k^{n-1}} = x_k - \frac{x_k}{n}+\frac{A}{n x_k^{n-1}} = \frac{1}{n} \left[{(n-1)x_k +\frac{A}{x_k^{n-1}}}\right]](/pictures/frwiki/98/bde3bc13ef9a97d25a6a46e832cfb31c.png)