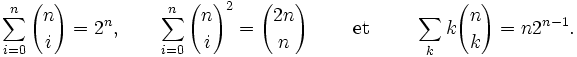Identités hypergéométriques

Les identités hypergéométriques sont des résultats sur des sommes de termes d'une série hypergéométrique. Ces identités apparaissent fréquemment dans des problèmes de combinatoire et d'analyse d'algorithme. Les premières identités ont été trouvées à la main par des mathématiciens brillants comme Carl Friedrich Gauss ou Ernst Kummer. Maintenant, l'objectif est d'obtenir des algorithmes qui automatisent les démonstrations de ces inégalités.

La liste des identités hypergéométriques est parfois appelée liste de Bailey suite à l'ouvrage de Bailey^[1].

Parmi les identités hypergéométriques les plus classiques

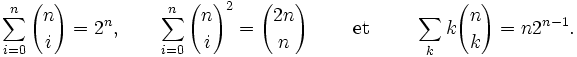
$\sum_{i=0}^{n} {n \choose i} = 2^{n}, \qquad \sum_{i=0}^{n} {n \choose i}^2 = {2n \choose n} \qquad \mbox{ et } \qquad\sum_{k} k {n \choose k} = n2^{n-1}.$

Automatisation de la preuve

La preuve automatisée repose sur deux étapes :

trouver une expression simple de la somme hypergéométrique, dans le meilleur des cas une forme close ;
montrer par A=B que cette expression est bien égale à la somme initiale.

Pour chaque type de somme hypergéométrique, il existe de nombreuses méthodes pour trouver une expression simple. Ces méthodes offrent aussi une preuve de l'égalité. On peut nommer :

pour les sommes définies : la méthode de sœur Celine Fasenmyer, l'algorithme de Zeilberger
pour les sommes indéfinies : l'algorithme de Gosper.

Les méthodes employées font souvent appel à des résultats du calcul formel.

Liens externes

(en) Marko Petkovšek, Herbert Wilf et Doron Zeilberger, A = B. Il s'agit d'un ouvrage explicitant un algorithme pour trouver une relation de récurrence à partir d'une identité. Faisant appel à un logiciel de calcul formel, tels Maple et Mathematica, l'algorithme a mis fin au besoin de tenir un catalogue d'identités et de relations de récurrence.
Sur l'algorithme de sœur Céline [pdf]
Exemples de fonctions spéciales

Référence

↑ W. N. Bailey, Generalized Hypergeometric Series, (1935) Cambridge Tracts in Mathematics and Mathematical Physics, No.32, Cambridge University Press, Cambridge.

Portail des mathématiques

Ce document provient de « Identit%C3%A9s hyperg%C3%A9om%C3%A9triques ».

Catégories : Analyse | Fonction hypergéométrique | Identité mathématique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Identités hypergéométriques de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Identites hypergeometriques — Identités hypergéométriques Les identités hypergéométriques sont des résultats sur des sommes de termes d une série hypergéométrique. Ces identités apparaissent fréquemment dans des problèmes de combinatoire et d analyse d algorithme. Les… … Wikipédia en Français
Identités Hypergéométriques — Les identités hypergéométriques sont des résultats sur des sommes de termes d une série hypergéométrique. Ces identités apparaissent fréquemment dans des problèmes de combinatoire et d analyse d algorithme. Les premières identités ont été… … Wikipédia en Français
Série hypergéométrique — En mathématiques, une série hypergéométrique est la somme d une suite de termes tels que le quotient du terme d indice k+1 par le terme d indice k est une fonction rationnelle de k. La série, lorsqu elle converge, définit une fonction… … Wikipédia en Français
Identité hypergéométrique — Une identité hypergéométrique est un résultat sur des sommes de termes d une série hypergéométrique. De telles identités apparaissent fréquemment dans des problèmes de combinatoire et d analyse d algorithme. Les premières identités ont été… … Wikipédia en Français
Fonction hypergéométrique — Série hypergéométrique En mathématiques, une série hypergéométrique est la somme d une suite de termes tels que le quotient du terme d indice k+1 par le terme d indice k est une fonction rationnelle de k. La série, lorsqu elle converge, définit… … Wikipédia en Français
Serie hypergeometrique — Série hypergéométrique En mathématiques, une série hypergéométrique est la somme d une suite de termes tels que le quotient du terme d indice k+1 par le terme d indice k est une fonction rationnelle de k. La série, lorsqu elle converge, définit… … Wikipédia en Français
Série hypergéometrique — Série hypergéométrique En mathématiques, une série hypergéométrique est la somme d une suite de termes tels que le quotient du terme d indice k+1 par le terme d indice k est une fonction rationnelle de k. La série, lorsqu elle converge, définit… … Wikipédia en Français
Doron Zeilberger — avec un T shirt décrivant une identité hypergéométrique[1]. Doron Zeilberger (en hébreu דורון ציילברגר) est un mathématicien et informaticien israélo américain né le 2 juille … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Mary Celine Fasenmyer — (4 octobre 1906, Crown 27 décembre 1996, Érié) est une mathématicienne de Pennsylvanie (États Unis), connue sous le nom de sœur Celine pour ses travaux sur les identités hypergéométriques. Ses deux seuls articles[1],[2], qui n … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Identités hypergéométriques