Hélicoïde
- Hélicoïde
-
Une hélicoïde est une surface s'appuyant sur une hélice et sur un axe. Elle fut découverte par Jean-Baptiste Marie Meusnier de La Place en 1776. C'est, avec le plan, la seule surface minimale réglée (c'est-à-dire pouvant être obtenue par déplacement d'une droite dans l'espace).
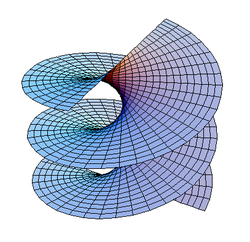
Une hélicoïde, tracée à l'aide de Mathematica

Une hélicoïde matérialisée par un film de savon s'appuyant sur une
hélice et son axe
Paramétrage :




C'est par ailleurs la seule famille de solutions de la forme z = f(v / u) à l'équation locale d'Euler-Lagrange qui caractérise les surfaces minimales.
On a longtemps cru que la caténoïde, l’hélicoïde et le plan étaient les seules surfaces minimales sans intersections. Depuis, les surfaces de Scherk ont prouvé que ce n'était pas le cas.
On peut matérialiser une hélicoïde, comme sur la photo ci-contre, en utilisant le fait qu'un film de savon, pour minimiser son énergie, doit minimiser sa surface : ainsi la bulle de savon s'accrochant à l'hélice et à la tige centrale est-elle la surface minimale passant par ces contours.
Voir aussi
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Hélicoïde de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
hélicoïde — [ elikɔid ] adj. et n. m. • 1704; gr. helikoeidês ♦ Géom. En forme d hélice. Parabole hélicoïde. ♢ N. m. Math. Un hélicoïde : surface engendrée par le mouvement hélicoïdal d une droite autour d un axe. Une vis est un hélicoïde. ● hélicoïde nom… … Encyclopédie Universelle
Helicoide — Hélicoïde Un hélicoïde est une surface s appuyant sur une hélice et sur un axe. Elle fut découverte par Jean Baptiste Marie Meusnier de la Place en 1776. C est, avec le plan, la seule surface minimale réglée (c est à dire pouvant être obtenue par … Wikipédia en Français
Hélicoide — Hélicoïde Un hélicoïde est une surface s appuyant sur une hélice et sur un axe. Elle fut découverte par Jean Baptiste Marie Meusnier de la Place en 1776. C est, avec le plan, la seule surface minimale réglée (c est à dire pouvant être obtenue par … Wikipédia en Français
helicóide — adj. 2 g. 1. O mesmo que helicoidal. • s. m. ou f. 2. [Geometria] Curva produzida pelo enrolamento da parábola à volta de um círculo. 3. [Geometria] Superfície produzida pelo movimento da linha à volta de um eixo. ♦ Grafia de helicoide antes… … Dicionário da Língua Portuguesa
helicoide — |ói| adj. 2 g. 1. O mesmo que helicoidal. • s. m. ou f. 2. [Geometria] Curva produzida pelo enrolamento da parábola à volta de um círculo. 3. [Geometria] Superfície produzida pelo movimento da linha à volta de um eixo … Dicionário da Língua Portuguesa
helicoide — sustantivo masculino 1. Área: geometría Superficie engendrada por una recta que se mueve apoyándose en una hélice y en el eje del cilindro sobre el que está trazada la hélice … Diccionario Salamanca de la Lengua Española
helicoide — (Del gr. ἑλικοειδής). m. Geom. Superficie alabeada engendrada por una recta que se mueve apoyándose en una hélice y en el eje del cilindro que la contiene, con el cual forma constantemente un mismo ángulo … Diccionario de la lengua española
hélicoïde — (é li ko i d ) adj. 1° Terme didactique. Qui ressemble à une hélice. Terme de géométrie. Parabole hélicoïde, courbe que produit la parabole ordinaire, quand on enroule son axe autour de la circonférence d un cercle. Terme d anatomie.… … Dictionnaire de la Langue Française d'Émile Littré
helicoide — ► sustantivo masculino GEOMETRÍA Superficie engendrada por una recta que se mueve apoyándose en una hélice fija. * * * helicoide (del gr. «hélix, ikos», espiral, y « oide») m. Superficie alabeada engendrada por una recta que se mueve apoyándose… … Enciclopedia Universal
Helicoide de Caracas — Hélicoïde de Caracas 10° 29′ 21″ N 66° 54′ 36″ W / 10.489167, 66.910083 … Wikipédia en Français







