- Fuzzy logic
-
Logique floue
La logique floue (fuzzy logic, en anglais) est une technique utilisée en intelligence artificielle. Elle a été formalisée par Lotfi Zadeh en 1965 et utilisée dans des domaines aussi variés que l'automatisme (freins ABS), la robotique (reconnaissance de formes), la gestion de la circulation routière (feux rouges), le contrôle aérien, l'environnement (météorologie, climatologie, sismologie, analyse du cycle de vie), la médecine (aide au diagnostic), l'assurance (sélection et prévention des risques) et bien d'autres. En fait, le simple fait de noter, déjà sous Jules Ferry, un élève dans différentes disciplines et de lui calculer un rang par application de coefficients à ses notes constituait déjà une certaine forme de logique floue.
Elle s'appuie sur la théorie mathématique des ensembles flous. Cette théorie, introduite par Zadeh, est une extension de la théorie des ensembles classiques pour la prise en compte d'ensembles définis de façon imprécise. C'est une théorie formelle et mathématique dans le sens où Zadeh, en partant du concept de fonction d'appartenance pour modéliser la définition d'un sous-ensemble d'un univers donné, a élaboré un modèle complet de propriétés et de définitions formelles. Il a aussi montré que cette théorie des sous-ensembles flous se réduit effectivement à la théorie des sous-ensembles classiques dans le cas où les fonctions d'appartenance considérées prennent des valeurs binaires ({0,1}).
Elle présente aussi l'intérêt d'être plus facile et meilleur marché à implémenter qu'une logique probabiliste, bien que cette dernière seule soit stricto sensu cohérente (voir Théorème de Cox-Jaynes). Par exemple la courbe Ev(p) peut être remplacée par trois segments de droite sans perte excessive de précision pour beaucoup d'applications considérées ci-dessus.
Sommaire
Principe
À l'inverse de la logique booléenne, la logique floue permet à une condition d'être en un autre état que vrai ou faux. Il y a des degrés dans la vérification d'une condition.
Considérons par exemple la vitesse d'un véhicule sur une route nationale française. La vitesse normale est de 90 km/h. Une vitesse peut être considérée comme élevée au-dessus de 100 km/h, et comme plus du tout élevée en dessous de 80 km/h.

fig. 1La logique booléenne envisagerait les choses de la manière suivante (voir fig. 1) :
- La vitesse est considérée à 100 % comme élevée à partir de 100 km/h, et à 0 % en dessous.
La logique floue, à l'inverse, permet des degrés de vérification de la condition « La vitesse est-elle élevée ? » (voir fig. 2) :
- La vitesse est considérée comme pas du tout élevée en dessous de 80 km/h. On peut donc dire qu'en dessous de 80 km/h, la vitesse est élevée à 0 %.
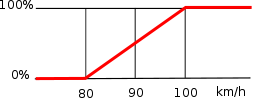
fig. 2- La vitesse est considérée comme élevée au-dessus de 100 km/h. La vitesse est donc élevée à 100 % au-dessus de 100 km/h.
- La vitesse est donc élevée à 50 % à 90 km/h, et à 25 % à 85 km/h.
De la même manière, la fonction « La vitesse est-elle peu élevée ? » sera évaluée de la manière suivante (voir fig. 3) :
- La vitesse est considérée comme peu élevée en dessous de 80 km/h. Elle est donc peu élevée à 100 %.

fig. 3- La vitesse est considérée comme pas du tout peu élevée au-dessus de 100 km/h. Elle est donc peu élevée à 0 %.
- La vitesse est donc peu élevée à 50 % à 90 km/h, et à 75 % à 95 km/h.
On peut également définir une fonction « La vitesse est-elle moyenne ? » (voir fig. 4) :
- La vitesse est moyenne à 90 km/h. À cette allure, la vitesse est moyenne à 100 %.
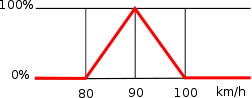
fig. 4- La vitesse n'est pas du tout moyenne en dessous de 80 km/h et au-dessus de 100 km/h. Hors de cet intervalle, la vitesse est moyenne à 0 %.
- La vitesse est donc moyenne à 50 % à 85 km/h et 95 km/h.
Il n'est pas obligatoire que la transition soit linéaire. Des transitions hyperboliques (comme une sigmoïde ou une tangente hyperbolique), exponentielle, gaussienne (dans le cas d'un état moyen) ou de toute autre nature sont utilisables (voir fig. 5).
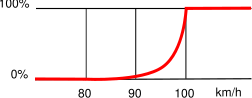
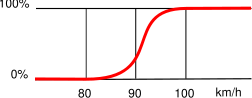
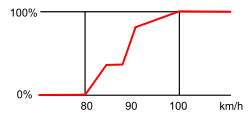
fig. 5Combinaison de plusieurs entrées
Dans le cas d'une combinaison de plusieurs entrées (« Si le ciel est bleu et si j'ai le temps »), deux cas se présentent :
- Les entrées sont liées par une fonction logique « ET » : dans ce cas, on peut considérer comme première approche seulement l'entrée ayant le degré de vérification le plus faible. En fait, il suffit de choisir un opérateur
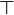 tel que
tel que  où
où 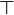 est appelée une t-norme. min est la plus optimiste des t-normes.
est appelée une t-norme. min est la plus optimiste des t-normes. - Les entrées sont liées par une fonction logique « OU » : dans ce cas, on peut considérer comme première approche seulement l'entrée ayant le degré de vérification le plus élevé. En fait, il suffit de choisir un opérateur
 tel que
tel que 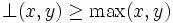 où
où  est appelée une t-conorme. max est la plus pessimiste des t-conormes.
est appelée une t-conorme. max est la plus pessimiste des t-conormes.
Il est techniquement possible de représenter toutes les opérations binaires de base en se basant sur la logique floue. En effet, à partir des opérateurs ET, OU et NON (AND, OR, NOT), on peut représenter les 8 opérations de base :
- OU (OR) : A OR B = max(A, B);
- ET (AND) : A AND B = min(A, B);
- NON (NOT) : NOT A = 1 - A;
- OU EXCLUSIF (XOR) : A XOR B = (A OR B) AND NOT (A AND B) = A + B - 2 × min(A, B);
- NON-OU (NOR) : A NOR B = 1 - max(A, B);
- NON-ET (NAND) : A NAND B = 1 - min(A, B);
- NON-XOR (NXR) : A NXR B = 1 + 2 × min(A, B) - (A + B);
- SUIVEUR (NOP) : NOP A = A.
Par ailleurs, la dimension décimale des variables de la logique floue permet d'effectuer des combinaisons non binaires :
- Le produit : A.B ou A × B (équivalent en binaire à l'opération AND)
- L'addition : A + B - A × B (équivalent en binaire à l'opération OR ; en effet, la simple addition dépasserait les bornes de l'interval [0 ; 1] dans certain cas)
Opérateurs flous
Les opérateurs flous (ou fuzzy) peuvent être implémentés de diverses manières et une même application peut d'ailleurs faire appel à des implémentations différentes judicieusement choisies selon le contexte.
L'exemple ci-dessous montre que, contrairement à une opinion parfois exprimée, le choix des opérateurs à utiliser n'est pas une simple question de goût ou d'inspiration du moment.
Exemple d'utilisation
Voici un exemple qui montre comment combiner des opérateurs flous (fuzzy) de divers types.
- l'exemple : confirmer l'appartenance d'une personne à un groupe
Une personne sera plus ou moins membre (à un niveau fzMembre, compris entre 0 et 1, inclusivement) d'un groupe, disons les flower lovers, soit si, pour n'importe quelle raison, elle en fait déjà plus ou moins partie (à un niveau fzDejaMembre), soit si elle a une assez bonne connaissance des orchidées (fzConnaitOrchidees) et que la connaissance des orchidées est un critère assez déterminant (fzOrchideesAmis) d'appartenance au groupe des flower lovers.
- une solution qui paraît bonne est :
fzMembre = Zadeh_OR( fzDejaMembre, Multiply_AND( fzConnaitOrchidees, fzOrchideesAmis ))
- et s'implémente comme :
fzMembre = max( fzDejaMembre, ( fzConnaitOrchidees * fzOrchideesAmis ))
pour fzDejaMembre=0 (faux), fzConnaitOrchidees=0.778 et fzOrchideesAmis=0.9, on trouve 0.7 pour fzDejaMembre=0.7, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on trouve 0.72 pour fzDejaMembre=0.72, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on retrouve 0.72 pour fzDejaMembre=0.72, fzConnaitOrchidees=0.5 et fzOrchideesAmis=0.9, on conserve 0.72 (ce qui est le résultat vraisemblablement attendu)
Autres solutions
- une solution qui n'utiliserait que les opérateurs de Zadeh serait :
fzMembre = Zadeh_OR( fzDejaMembre, Zadeh_AND( fzConnaitOrchidees, fzOrchideesAmis ))
fzMembre = max( fzDejaMembre, min( fzConnaitOrchidees, fzOrchideesAmis ))
pour fzDejaMembre=0 (faux), fzConnaitOrchidees=0.778 et fzOrchideesAmis=1 (vrai), on trouve 0.778 pour fzDejaMembre=0 (faux), fzConnaitOrchidees=0.778 et fzOrchideesAmis=0.9, on trouve aussi 0.778 (ce qui est trop élevé) pour fzDejaMembre=0.778, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on trouve 0.8 pour fzDejaMembre=0.8, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on retrouve 0.8 pour fzDejaMembre=0.8, fzConnaitOrchidees=0.5 et fzOrchideesAmis=0.9, on conserve 0.8 (ce qui est stable mais trop élevé)
- une solution qui n'utiliserait que les opérateurs représentables par des paraboloïdes hyperboliques serait :
fzMembre = Add_OR( fzDejaMembre, Multiply_AND( fzConnaitOrchidees, fzOrchideesAmis ))
fzMembre = fzDejaMembre + (fzConnaitOrchidees*fzOrchideesAmis) - (fzDejaMembre*fzConnaitOrchidees*fzOrchideesAmis)
pour fzDejaMembre=0 (faux), fzConnaitOrchidees=0.778 et fzOrchideesAmis=0.9, on trouve 0.7 pour fzDejaMembre=0.7, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on trouve 0.916 (ce qui est sûrement trop élevé) pour fzDejaMembre=0.916, fzConnaitOrchidees=0.8 et fzOrchideesAmis=0.9, on trouve 0,97648 (ce qui est instable et sûrement beaucoup trop élevé) pour fzDejaMembre=0,97648, fzConnaitOrchidees=0.5 et fzOrchideesAmis=0.9, on trouve 0. 987 064 (une augmentation bien malvenue)
Convergence
Les trois méthodes exposées ci-dessus convergent lorsque les valeurs d'entrée sont booléennes
pour fzDejaMembre=0 (faux), fzConnaitOrchidees=0 (faux) et fzOrchideesAmis=1 (vrai), on trouve 0 (faux) pour fzDejaMembre=0 (faux), fzConnaitOrchidees=1 (vrai) et fzOrchideesAmis=1 (vrai), on trouve 1 (vrai) pour fzDejaMembre=1 (vrai), fzConnaitOrchidees=1 (vrai) et fzOrchideesAmis=1 (vrai), on retrouve 1 (vrai) pour fzDejaMembre=1 (vrai), fzConnaitOrchidees=0 (faux) et fzOrchideesAmis=1 (vrai), on conserve 1 (vrai)
Opérateur implique
Pour l'exemple à l'orchidée ci-dessus, une situation normale est que la connaissance des orchidées implique l'appartenance au groupe. C’est-à-dire, plus précisément, qu'on ne peut pas connaître les orchidées et, simultanément, ne pas être membre du groupe des amis des fleurs.
fzImpliqueOk = NOT( AND( fzConnaitOrchidees, NOT( fzMembre ) ) )
De même qu'on a vu ci-dessus plusieurs manières d'implémenter les opérateurs OR et AND, il y a aussi plusieurs manières d'implémenter la notion d'implication.
fzImpliqueOk = Bool_IMPLIES( fzConnaitOrchidees, fzMembre ) fzImpliqueOk = Zadeh_IMPLIES( fzConnaitOrchidees, fzMembre ) fzImpliqueOk = HypPar_IMPLIES( fzConnaitOrchidees, fzMembre )
Implémentation
Les opérateurs ci-dessus s'implémenteront respectivement comme ceci :
fzImpliqueOk = fzConnaitOrchidees ⇐ fzMembre fzImpliqueOk = 1 - min( fzConnaitOrchidees, (1 - fzMembre) ) fzImpliqueOk = 1 - fzConnaitOrchidees + (fzConnaitOrchidees*fzMembre
dans un cas extrême mais normal, avec fzConnaitOrchidees=0.8 et fzMembre=0.995, les valeurs trouvées seront respectivement
1 (true) 0.995 (Zadeh) 0.996 (Hyperbolic Paraboloid)
dans un cas considéré comme normal, avec fzConnaitOrchidees=0.8 et fzMembre=0.72, les valeurs trouvées seront respectivement
0 (false) (la personne est moins membre qu'elle ne connait) 0.72 (Zadeh) 0.776 (Hyperbolic Paraboloid)
dans un autre cas qui reste normal, la personne pouvant aussi être membre des amis des fleurs à cause de son amour des tulipes, avec fzConnaitOrchidees=0.66 et fzMembre=0.72, les valeurs trouvées seront respectivement
1 (true) (la personne est plus membre qu'elle ne connait) 0.72 (Zadeh) 0.772 (Hyperbolic Paraboloid)
dans un cas assez douteux, avec fzConnaitOrchidees=0.5 et fzMembre=0.5, les valeurs trouvées seront respectivement
1 (true) 0.5 (Zadeh) 0.75 (Hyperbolic Paraboloid)
dans un cas anormal, avec fzConnaitOrchidees=0.8 et fzMembre=0.3, les valeurs trouvées seront respectivement
0 (false) 0.3 (Zadeh) 0.44 (Hyperbolic Paraboloid)
dans un cas anormal et extrême, avec fzConnaitOrchidees=0.8 et fzMembre=0.005, les valeurs trouvées seront respectivement
0 (false) 0.2 (Zadeh) 0.204 (Hyperbolic Paraboloid)
Utilisation pratique
Une application informatique qui viserait à proposer à un opérateur humain de traiter les cas anormaux en commençant par les plus suspects utiliserait les valeurs indiquées ci-dessus en gras et obtenues par la méthode identifiée Hyperbolic Paraboloid, particulièrement discriminante.
Il n'est pas sûr que cette application intéresse les amis des fleurs. Par contre, l'intérêt pour un service de médecine préventive (ou même pour un fleuriste) est compréhensible. Lorsque le nombre d'examens des cas suspects doit être plafonné (par exemple pour des raisons de temps, de coût, de dangerosité, etc), une préclassement intelligent, fondé -sinon sur une théorie incontestée- du moins sur une technologie opérationnelle, peut s'avérer utile.
Représentation graphique
L'article commons:Fuzzy operator fournit de nombreuses représentations graphiques de quelques implémentations possibles des opérateurs fuzzy. On trouvera ci-dessous, à titre d'exemple, la représentation de huit implémentations différentes d'une opération qui viserait à apprécier la simultanéité de deux faits (jugés de poids équivalents dans les six images à gauche mais de poids différents dans les deux images de droite).
Commande floue
Une fois la valeur de l'entrée (« La vitesse est-elle élevée ? ») évaluée, une valeur peut être déterminée pour une fonction de sortie. Considérons la fonction « Si la fièvre est forte, alors administrer de l'aspirine ». Une telle fonction est appelée commande floue. Elle est composée de deux parties :
- Une entrée : « La fièvre est-elle forte ? ». On considère qu'une fièvre n'est pas forte en dessous de 38 °C, et qu'elle est forte au-dessus de 40 °C.
- Une sortie : « Administrer de l'aspirine »
Ces deux parties sont liées. On peut les représenter ensemble comme sur la fig. 6.
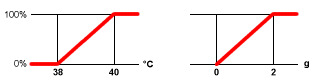
fig. 6Il existe plusieurs techniques pour déterminer la valeur de la sortie (dans l'exemple : la quantité d'aspirine à administrer) :
- La droite ayant la même ordonnée que le point de la courbe de départ ayant pour abscisse la valeur de l'entrée coupe la courbe de sortie. L'abscisse de ce point d'intersection est une valeur de sortie possible (fig. 7).
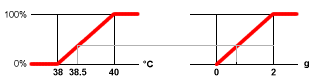
fig. 7- La droite ayant la même ordonnée que le point de la courbe de départ ayant pour abscisse la valeur de l'entrée délimite un trapèze au niveau de la sortie. Le centre de gravité de ce trapèze est également une valeur de sortie possible (fig. 8).
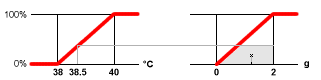
fig. 8Insuffisances en tant que théorie ?
On rencontre souvent l'opinion qui dit que "La théorie des ensembles flous présente la particularité de n'avoir aucun théorème à proposer. C'est-à-dire que si elle peut rendre quelques services techniques, elle ne peut pour autant prétendre à un quelconque statut de science, et encore moins de théorie.".
En fait, la logique floue a été formalisée et des théorèmes permettent de faire le pont entre la logique classique et la logique floue et montrent que dans le cas particulier où les propositions traitées ne sont pas floues, la logique floue se réduit à la logique classique Fuzzy Logic. Reste à savoir si ces théorèmes sont difficiles.
D'autre part, si certains prétendent que le théorème de Cox-Jaynes montre que:
- l'on peut représenter un état de connaissance floue par une probabilité;
- tout moyen utilisé pour prendre des décisions sera soit isomorphe à la théorie des probabilités, soit incohérent.
On peut douter que le théorème de Cox-Jaynes s'applique ici de telle manière à des connaissances floues. En effet, on notera qu'une connaissance floue n'est généralement pas une connaissance 'incertaine' et n'est donc pas reliée à une probabilité (ce qui rend difficile, voire injustifié, dans ces cas-là sa représentation en tant que probabilité).
Le flou est lié à la forme de la connaissance: son imprécision donc, et n'est donc pas de nature probabiliste. Par exemple, dire "l'âge de cette personne est autour de 30 ans" ne présume en rien de la probabilité de l'âge effectif de la personne. On peut mieux voir la distinction entre imprécision et probabilité en pondérant cette assertion: "je suis sûr que l'âge de cette personne est autour de 30 ans" où l'on peut retrouver ici à la fois une imprécision (sur la valeur de l'âge) et une certitude (sur le fait que cet âge soit autour de 30 ans). Ou aussi: "l'âge de cette personne est autour de 30 ans, avec une probabilité de 0.2" où l'on retrouve encore une connaissance floue ("autour de 30 ans") qui est relativisée par une probabilité de véracité.
Comme on peut le voir, la logique floue s'attache donc à une certaine forme des connaissances (leur imprécision) et propose un formalisme rigoureux (cf. les travaux des théoriciens de la logique floue) afin d'inférer de nouvelles connaissances. En cela, elle est complémentaire de la théorie des probabilités.
Pour illustrer encore ce propos, on peut citer l'exemple classique de Jim Bezdek qui permet de mieux différencier probabilité et imprécision: "On se trouve dans un désert, après des jours d'errance… Presque mort de soif, on trouve alors 2 bouteilles remplies d'un liquide. Sur la bouteille A, une étiquette annonce "potable avec un degré 0.9", et sur la bouteille B, l'étiquette dit "potable avec une probabilité 0.9". Laquelle de ces 2 bouteilles peut on boire?". Si l'on traduit les indications des étiquettes, on en retire qu'en buvant la bouteille A, on pourra s'en tirer avec comme seuls risques, quelques problèmes intestinaux non mortels… Par contre, en buvant la bouteille B, il y a une probabilité non négligeable (10% de chance) que le liquide puisse être très nocif (acide…) et absolument pas buvable.
La théorie des possibilités a été introduite (aussi par Lotfi Zadeh en 1978) afin de permettre la prise en compte combinée à la fois de l'imprécision et de l'incertitude dans des connaissances.
La logique floue n'est pas la seule à parler d'incertitude
La logique modale a été introduite par Aristote, puis continuée par Leibniz et des chercheurs contemporains pour prendre en compte des affaiblissements ou des renforcements d'affirmations présents dans les langues naturelles.
La théorie de la complexité algorithmique (ou complexité de Kolmogorov) est aussi une méthode mathématiquement rigoureuse pour envisager la difficulté de donner la description précise d'une chose.
Enfin, les probabilités bayésiennes utilisés en avenir incertain utilisent des approches voisines de celles de la logique floue.
Voir aussi
- Ensemble flou
- Information Partielle Linéaire
- Théorie du prototype (sémantique cognitive)
- Portail de la logique
- Portail des mathématiques
- Portail de l’informatique
Catégories : Logique | Intelligence artificielle | Automatique
Wikimedia Foundation. 2010.












