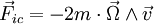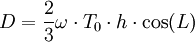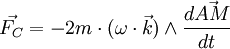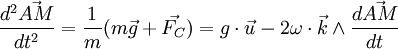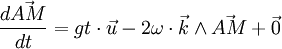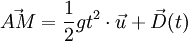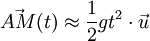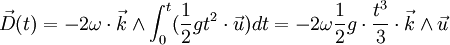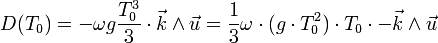Formule de la déviation vers l'est

Déviation vers l'est

La déviation vers l'est est un phénomène physique correspondant au fait qu'un corps en chute libre ne suit pas exactement la direction de la pesanteur, mais est légèrement dévié vers l'est par la force de Coriolis résultant de la rotation de la Terre. Ce phénomène a été mis en évidence par Ferdinand Reich en 1833, à la suite des travaux de Coriolis sur l'utilisation des forces d'inertie dans un référentiel non inertiel. Reich fit tomber des projectiles dans un puits de 158m de profondeur à Freiberg (Saxe). Il observa une déviation de 28mm vers l'est.

Sommaire

1 Histoire
2 Expression
3 Formule de déviation vers l'est
- 3.1 Équation rigoureuse
- 3.2 Approximation du premier ordre
4 Compléments
5 Bibliographie
6 Voir aussi

Histoire

Huygens (1629-1695) qui était sur la piste de la force de Coriolis avec sa théorie de la relativité totale, n'a pas fait le poids face à Isaac Newton et ses notions de temps et d'espace absolu. Ce dernier étouffa par la monumentalité de son œuvre toute tentative relativiste, et il ne voulait pas manier les forces d'inertie. La force de Coriolis (1792-1843) ne sera énoncée que tardivement au XIX^e siècle.

Newton a fait la démonstration de la déviation vers l'est en 1679 dans le référentiel « absolu » géocentrique. Pour faire simple, prenons le cas équatorial. Il remarque, mais il n'était pas le premier à le faire, que le point A avait une vitesse ω·(R + h), soit une vitesse plus grande que la vitesse du point O situé sur le sol à la verticale descendante de A. Cette différence de vitesse correspond à une petite vitesse vers l'est de ω·h, donc la déviation vers l'est est simplement ω·h·T₀.

Il se trompait ainsi d'un facteur 2/3. Il le prit vite en compte en comprenant que, au cours d'une aussi longue trajectoire, il fallait compter avec le changement de direction de la pesanteur, sur une terre ronde et non plate : la trajectoire n'est donc pas parabolique.

Expression

La déviation vers l'est est un cas particulier de la force de Coriolis appliquée à un corps en chute dans l'atmosphère de la Terre, dont la formule est donnée par :

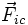$\vec{F}_{ic} = -2m \cdot \vec{\Omega}\wedge \vec{v}$

où :

$\vec{F}_{ic}$ est la force d'inertie de Coriolis;
$m$ est la masse du corps en chute;
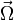$\vec{\Omega}$ est le vecteur vitesse angulaire instantanée de rotation de la Terre;
$\vec{v}$ la vitesse instantanée du corps.

Le vecteur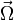 $\vec{\Omega}$ étant parallèle à l'axe de rotation de la Terre, dirigé vers le nord, et $\vec{v}$ orienté vers le centre de la Terre, le produit vectoriel résultant est orienté vers l'est (une fois inversé). Cette force est proportionnelle à la latitude de l'objet, sa masse et sa vitesse de chute.

Le calcul de cette force nécessite la résolution d'une équation différentielle qui n'a pas de solution mathématique rigoureuse. Il faut alors trouver une solution approchée à l'aide de la méthode perturbative : dans un premier temps, on résout l'équation sans la force de Coriolis, puis on rajoute une force de Coriolis dérivant de la solution précédente, et ainsi de suite. La convergence vers la bonne solution est alors très rapide : 3 itérations du procédé suffisent largement.

Formule de déviation vers l'est

La formule de déviation vers l'est est une forme simplifiée de la représentation vectorielle qui permet de calculer la déviation vers l'est d'un corps en chute libre dans l'atmosphère terrestre; cette déviation est une conséquence de la Force de Coriolis qui apparait dans les équations, car la terre en rotation sur elle-même n'est pas un repère galiléen. Cette déviation est maximale à l'équateur et nulle aux pôles.

La longueur de cette déviation est donnée par la formule approchée :

$D = \frac{2}{3}\omega \cdot T_0 \cdot h \cdot \cos(L)$

où :

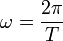$\omega = \frac{2\pi}{T}$ représente la vitesse angulaire de rotation de la terre,
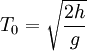$T_0=\sqrt{\frac{2h}{g}}$ est le temps de la chute,
h est la hauteur de la chute,
$L$ la latitude à laquelle est effectuée l'expérience (0 à l'équateur, 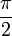$\frac{\pi}{2}$ aux pôles).

Équation rigoureuse

On part de la représentation vectorielle de la force de Coriolis, et on remplace le vecteur vitesse par la dérivée du vecteur position :

$\vec{F_C} = - 2m \cdot (\omega \cdot \vec{k}) \wedge \frac {d\vec{AM}}{dt}$

où :

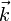$\vec{k}$ est parallèle à l'axe de rotation de la Terre, orienté vers le nord;
A est le point d'origine, référentiel tournant lié à la surface de la Terre.

Le principe fondamental de la dynamique permet d'écrire l'accélération comme somme de la force d'attraction de la Terre et de la force de Coriolis :

$\frac{d^2\vec{AM}}{dt^2} = \frac{1}{m} ( m \vec{g} + \vec{F_C} ) = g \cdot \vec{u} - 2 \omega \cdot \vec{k} \wedge \frac {d\vec{AM}}{dt}$

où $\vec{u}$ est dirigé selon la verticale descendante.

On intègre une fois pour trouver la vitesse :

$\frac{d\vec{AM}}{dt} = gt \cdot \vec{u} - 2 \omega \cdot \vec{k}\wedge \vec{AM} + \vec{0}$

la vitesse initiale étant nulle.

On intègre à nouveau pour obtenir la position du corps en fonction du temps :

$\vec{AM} = \frac{1}{2}gt^2 \cdot \vec{u} + \vec{D}(t)$

où la déviation est donnée par : 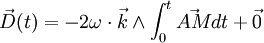$\vec{D}(t) = - 2\omega \cdot \vec{k}\wedge\int_0^t\vec{AM}dt + \vec{0}$ (car A est l'origine).

Approximation du premier ordre

La déviation vers l'est étant petite devant la déviation due à la pesanteur, on prend comme approximation :

$\vec{AM}(t) \approx \frac{1}{2}gt^2 \cdot \vec{u}$

d'où le résultat :

$\vec{D}(t) = -2\omega \cdot \vec{k} \wedge \int_0^t (\frac{1}{2}gt^2 \cdot \vec{u}) dt = -2\omega\frac{1}{2}g \cdot \frac{t^3}{3} \cdot \vec{k}\wedge \vec{u}$

qui est valide si D est petit devant h, c’est-à-dire pour T₀ (temps de chute) petit devant T = 86 164 s (période sidérale) :

$D(T_0) = -\omega g \frac{T_0^3}{3} \cdot \vec{k} \wedge \vec{u} = \frac{1}{3} \omega \cdot (g \cdot T_0^2) \cdot T_0 \cdot - \vec{k} \wedge \vec{u}$

soit, en valeur absolue :

$D = \frac{2}{3}\omega \cdot T_0 \cdot h \cdot \cos(L)$

Compléments

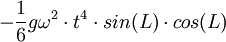Un autre terme, encore plus faible, donne une déviation vers le sud dans l'hémisphère nord, et vers le nord dans l'hémisphère sud : il vaut $-\frac{1}{6}g\omega^2 \cdot t^4 \cdot sin(L) \cdot cos(L)$ .
Une grande question que se posaient les théoriciens : en réduisant la terre à un point massique central, quelle serait la déviation sur une chute de R = 6 400 km ? En utilisant l'ellipse de Kepler, on trouve : D = paramètre de l'ellipse = R·(1/17)² = R/289 soit environ 22 kilomètres.
On peut remarquer la parenté de l'équation de la force de Coriolis avec celle de l'effet Hall en électricité.

Bibliographie

Lev Landau & Evguéni Lifchitz ; Cours de physique théorique - Tome 1 : Mécanique, Mir (4^e édition-1982), ISBN 5-03-000198-0.

Voir aussi

Portail de la physique

Ce document provient de « D%C3%A9viation vers l%27est ».

Catégories : Équation différentielle | Mécanique classique | Méthode mathématique de la physique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Formule de la déviation vers l'est de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Formule De La Déviation Vers L'est — Déviation vers l est La déviation vers l est est un phénomène physique correspondant au fait qu un corps en chute libre ne suit pas exactement la direction de la pesanteur, mais est légèrement dévié vers l est par la force de Coriolis résultant… … Wikipédia en Français
Formule de la deviation vers l'est — Déviation vers l est La déviation vers l est est un phénomène physique correspondant au fait qu un corps en chute libre ne suit pas exactement la direction de la pesanteur, mais est légèrement dévié vers l est par la force de Coriolis résultant… … Wikipédia en Français
Formule de déviation vers l'est — Déviation vers l est La déviation vers l est est un phénomène physique correspondant au fait qu un corps en chute libre ne suit pas exactement la direction de la pesanteur, mais est légèrement dévié vers l est par la force de Coriolis résultant… … Wikipédia en Français
Deviation vers l'est — Déviation vers l est La déviation vers l est est un phénomène physique correspondant au fait qu un corps en chute libre ne suit pas exactement la direction de la pesanteur, mais est légèrement dévié vers l est par la force de Coriolis résultant… … Wikipédia en Français
Déviation Vers L'est — La déviation vers l est est un phénomène physique correspondant au fait qu un corps en chute libre ne suit pas exactement la direction de la pesanteur, mais est légèrement dévié vers l est par la force de Coriolis résultant de la rotation de la… … Wikipédia en Français
Déviation vers l'Est — La déviation vers l est est un phénomène physique correspondant au fait qu un corps en chute libre ne suit pas exactement la direction de la pesanteur, mais est légèrement dévié vers l est par la force de Coriolis résultant de la rotation de la… … Wikipédia en Français
Déviation vers l'est — La déviation vers l est est un phénomène physique correspondant au fait qu un corps en chute libre ne suit pas exactement la direction de la pesanteur, mais est légèrement dévié vers l est par la force de Coriolis résultant de la rotation de la… … Wikipédia en Français
Déviation standard — Écart type En mathématiques, plus précisément en statistiques et probabilités, l écart type mesure la dispersion d une série de valeurs autour de leur moyenne. Dans le domaine des probabilités, l écart type est une quantité réelle positive,… … Wikipédia en Français
Est-Montréal — Montréal Pour les articles homonymes, voir Montréal (homonymie). Montréal … Wikipédia en Français
Est de Montréal — Montréal Pour les articles homonymes, voir Montréal (homonymie). Montréal … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Formule de la déviation vers l'est

Déviation vers l'est

Sommaire

Histoire

Expression