Formule de Héron

Formule de Héron
Notations usuelles dans un triangle

En géométrie euclidienne, la formule de Héron, du nom de Héron d'Alexandrie, permet de calculer l'aire d'un triangle quelconque en ne connaissant que les longueurs des trois côtés du triangle :

A = \sqrt{s(s-a)(s-b)(s-c)}

avec

s = \frac 12 (a+b+c) \,

s est le demi-périmètre du triangle, a, b et c sont les longueurs des côtés du triangle et A est l'aire du triangle.

Sommaire

Démonstration

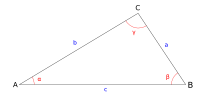
La formule de Héron peut se déduire de manière calculatoire du théorème d'Al-Kashi en utilisant

\cos\gamma = \frac{a^2+b^2-c^2}{2ab}

puis la formule classique de l'aire du triangle donnée par cet angle et les côtés adjacents :

A \, = \frac 12 ab\sin\gamma\,
=\frac 12ab\sqrt{1-\cos^2\gamma}\,
=\frac 12 ab\sqrt{(1-\cos\gamma)(1+\cos\gamma)}\,
=\frac12ab\sqrt{\left(1-\frac{c^2-a^2-b^2}{2ab}\right)\left(1+\frac{c^2-a^2-b^2}{2ab}\right)}
=\frac14\sqrt{\left((a+b)^2-c^2\right)\left(c^2-(a-b)^2\right)}
=\frac14\sqrt{(a+b+c)(a+b-c)(-a+b+c)(a-b+c)}\,

On obtient la formule de Héron en substituant

a = 2s-b-c\,

dans la formule ci-dessus.

Variantes

D'après les calculs intermédiaires ci-dessus, on a aussi :

\begin{align}16A^2&=(a+b+c)(a+b-c)(-a+b+c)(a-b+c)\\&=2(a^2 b^2+a^2c^2+b^2c^2)-(a^4+b^4+c^4)\\&=(a^2 + b^2 + c^2)^2 - 2(a^4 + b^4 + c^4)~.\end{align}

Mise en œuvre numérique

La formule de Héron présente une instabilité lors du calcul numérique, qui se manifeste pour les triangles en épingle, c'est-à-dire dont un côté est de dimension très petite par rapport aux autres (confrontation de petites et grandes valeurs).

En choisissant les noms de côtés de sorte à ce que a > b > c\, et en réorganisant les termes de façon à optimiser les grandeurs ajoutées ou soustraites, on obtient la formule de Kahan, plus stable :

A = \frac14 \sqrt{\left(a+(b+c)\right)\left(c-(a-b)\right)\left(c+(a-b)\right)\left(a+(b-c)\right)}\,.

Généralisation

En géométrie sphérique

En trigonométrie sphérique, il existe une formule analogue à la formule de Héron qui permet de déduire l'aire d'un triangle sphérique à partir de ses côtés : elle est donnée par le théorème de l'Huilier.

Pour les quadrilatères

Il existe des formulations analogues pour déterminer l'aire d'un quadrilatère, mais à moins qu'il soit inscriptible dans un cercle, la donnée supplémentaire d'angles ou des diagonales est nécessaire. Voir : Formule de Bretschneider (en) et Formule de Brahmagupta.

Pour les tétraèdres

Le volume d'un tétraèdre est donné en fonction de la longueur de ses arêtes par le déterminant de Cayley-Menger (en).

Voir aussi

Articles connexes

Liens externes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Formule de Héron de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Formule De Héron — Notations usuelles dans un triangle En géométrie euclidienne, la formule de Héron, trouvée par Héron d Alexandrie, permet de calculer l aire d un triangle quelconque en ne connaissant que les longueurs des trois côtés du triangle  …   Wikipédia en Français

  • Formule de Heron — Formule de Héron Notations usuelles dans un triangle En géométrie euclidienne, la formule de Héron, trouvée par Héron d Alexandrie, permet de calculer l aire d un triangle quelconque en ne connaissant que les longueurs des trois côtés du… …   Wikipédia en Français

  • Formule de héron — Notations usuelles dans un triangle En géométrie euclidienne, la formule de Héron, trouvée par Héron d Alexandrie, permet de calculer l aire d un triangle quelconque en ne connaissant que les longueurs des trois côtés du triangle  …   Wikipédia en Français

  • Heron d'Alexandrie — Héron d Alexandrie  Cet article concerne un savant grec. Pour les oiseaux échassiers, voir Héron. Héron d Alexandrie Naissance …   Wikipédia en Français

  • Héron L'Ancien — Héron d Alexandrie  Cet article concerne un savant grec. Pour les oiseaux échassiers, voir Héron. Héron d Alexandrie Naissance …   Wikipédia en Français

  • Héron d'alexandrie —  Cet article concerne un savant grec. Pour les oiseaux échassiers, voir Héron. Héron d Alexandrie Naissance …   Wikipédia en Français

  • Formule Brahmagupta — Formule de Brahmagupta En géométrie euclidienne, la formule de Brahmagupta, trouvée par Brahmagupta, est une généralisation de la formule de Héron à l aire d un quadrilatère convexe dont les sommets se situent sur un même cercle, en ne… …   Wikipédia en Français

  • Formule De Brahmagupta — En géométrie euclidienne, la formule de Brahmagupta, trouvée par Brahmagupta, est une généralisation de la formule de Héron à l aire d un quadrilatère convexe dont les sommets se situent sur un même cercle, en ne connaissant que la longueur de… …   Wikipédia en Français

  • Formule de brahmagupta — En géométrie euclidienne, la formule de Brahmagupta, trouvée par Brahmagupta, est une généralisation de la formule de Héron à l aire d un quadrilatère convexe dont les sommets se situent sur un même cercle, en ne connaissant que la longueur de… …   Wikipédia en Français

  • Héron d'Alexandrie — Cet article concerne un savant grec. Pour les oiseaux échassiers, voir Héron. Héron d Alexandrie Naissance Ier siècle a …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”