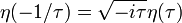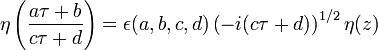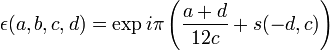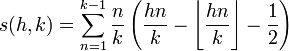Fonction eta de Dedekind

Fonction eta de Dedekind

Fonction êta de Dedekind

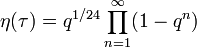
La fonction êta de Dedekind est une fonction définie sur le demi-plan de Poincaré formé par les nombres complexes de partie imaginaire positive. Pour chaque nombre complexe τ dans cet ensemble, on définit q = e2iπτ et la fonction êta est alors : \eta(\tau) = q^{1/24} \prod_{n=1}^{\infty} (1-q^{n})

La fonction êta est holomorphe dans le demi-plan supérieur mais n'admet pas de prolongement analytique en dehors de cet ensemble.

La fonction êta vérifie les équations fonctionnelles :

η(τ + 1) = exp(2πi / 24)η(τ)
\eta(-1/\tau) = \sqrt {-i\tau} \eta(\tau)

Plus généralement,

\eta \left( \frac{a\tau+b}{c\tau+d} \right) = \epsilon (a,b,c,d) \left( -i(c\tau+d) \right)^{1/2} \eta(z)

où a,b,c,d sont des entiers tels que ad-bc=1, qui sont donc associés à une transformation appartenant au groupe modulaire, et

\epsilon (a,b,c,d)=\exp i\pi \left( \frac{a+d}{12c} + s(-d,c) \right)

où s(h,k) est la somme de Dedekind

s(h,k)=\sum_{n=1}^{k-1} \frac{n}{k} \left( \frac{hn}{k} - \left\lfloor \frac{hn}{k} \right\rfloor -\frac{1}{2} \right)

A cause des équations fonctionnelles, la fonction êta est une forme modulaire de poids 1/2. On peut s' en servir pour définir d'autres formes modulaires. En particulier, le discriminant modulaire de Weierstrass peut être défini comme

Δ(τ) = (2π)12η(τ)24.

La fonction Δ est une forme modulaire de poids 12. Comme la fonction êta est facile à calculer, il est souvent utile d'exprimer, quand c'est possible, d'autres fonctions comme produits et quotients de fonctions êta. Ceci est possible pour beaucoup de formes modulaires.

Références

  • Jean-Pierre Serre, Cours d'arithmétique [détail des éditions]
  • Tom M. Apostol, Modular functions and Dirichlet Series in Number Theory (1990), Springer-Verlag, New York. ISBN 0-387-97127-0 Voir chapitre 3.
Ce document provient de « Fonction %C3%AAta de Dedekind ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction eta de Dedekind de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Fonction Eta De Dedekind — Fonction êta de Dedekind La fonction êta de Dedekind est une fonction définie sur le demi plan de Poincaré formé par les nombres complexes de partie imaginaire positive. Pour chaque nombre complexe τ dans cet ensemble, on définit q = e2iπτ et la… …   Wikipédia en Français

  • Fonction eta de dedekind — Fonction êta de Dedekind La fonction êta de Dedekind est une fonction définie sur le demi plan de Poincaré formé par les nombres complexes de partie imaginaire positive. Pour chaque nombre complexe τ dans cet ensemble, on définit q = e2iπτ et la… …   Wikipédia en Français

  • Fonction êta de Dedekind — La fonction êta de Dedekind est une fonction définie sur le demi plan de Poincaré formé par les nombres complexes de partie imaginaire positive. Pour chaque nombre complexe τ dans cet ensemble, on définit q = e2iπτ et la fonction êta est… …   Wikipédia en Français

  • Fonction Theta — Fonction thêta En mathématiques, on appelle fonctions thêta certaines fonctions spéciales d une ou de plusieurs variables complexes. Elles apparaissent dans plusieurs domaines, comme l étude des variétés abéliennes, des espace de modules, et les… …   Wikipédia en Français

  • Fonction theta — Fonction thêta En mathématiques, on appelle fonctions thêta certaines fonctions spéciales d une ou de plusieurs variables complexes. Elles apparaissent dans plusieurs domaines, comme l étude des variétés abéliennes, des espace de modules, et les… …   Wikipédia en Français

  • Fonction théta — Fonction thêta En mathématiques, on appelle fonctions thêta certaines fonctions spéciales d une ou de plusieurs variables complexes. Elles apparaissent dans plusieurs domaines, comme l étude des variétés abéliennes, des espace de modules, et les… …   Wikipédia en Français

  • Fonction thêta — Fonction theta de Jacobi θ1 avec u = iπz et q = eiπτ = 0.1e0.1iπ. Par convention (mathematica) …   Wikipédia en Français

  • Fonction Zeta — Fonction zêta Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La fonction zêta (d après la lettre grecque zêta, ou ζ) est le nom de nombreuses fonctions en mathématiques. La plus connue est la fonction… …   Wikipédia en Français

  • Fonction dzêta — Fonction zêta Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La fonction zêta (d après la lettre grecque zêta, ou ζ) est le nom de nombreuses fonctions en mathématiques. La plus connue est la fonction… …   Wikipédia en Français

  • Fonction zeta — Fonction zêta Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La fonction zêta (d après la lettre grecque zêta, ou ζ) est le nom de nombreuses fonctions en mathématiques. La plus connue est la fonction… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”