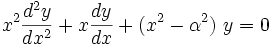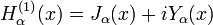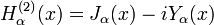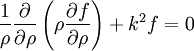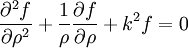Fonction de hankel

Fonction de Hankel

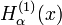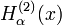Les fonctions de Hankel, du nom du mathématicien Hermann Hankel, notées $H_{\alpha}^{(1)}(x)$ et $H_{\alpha}^{(2)}(x)$ , sont des fonctions spéciales de la physique mathématique. Ce sont les solutions linéairement indépendantes de l'équation de Bessel:

$x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} + (x^2 - \alpha^2) \ y = 0$

où α est un nombre arbitraire réel ou complexe. Dans le cas où α est un entier, on le note alors généralement par n dans l'équation de Bessel, et il est dénommé ordre.

Fonction de Hankel du premier type:

$H_{\alpha}^{(1)}(x) = J_{\alpha}(x) + i Y_{\alpha}(x)$

Fonction de Hankel du deuxième type:

$H_{\alpha}^{(2)}(x) = J_{\alpha}(x) - i Y_{\alpha}(x)$

La présence de i montre qu'il s'agit de solutions complexes. Les fonctions de Hankel sont des combinaisons linéaires des 2 autres solutions de l'équation de Bessel que sont $J α (x)$ et $Y α (x)$ , dites fonctions de Bessel de première et deuxième espèce. Les fonctions de Hankel sont par conséquent aussi nommées Fonctions de Bessel de troisième espèce.

Utilité

Les fonctions de Hankel du premier ou deuxième type sont utilisées pour exprimer en physiques des ondes cylindriques entrantes ou sortantes. Par exemple, dans un problème de diffraction par un cylindre infiniment long et éclairé par une onde plane, l'équation de Helmholtz en coordonnées cylindrique ( $ρ,θ, z$ ) mènera à l'équation de Bessel décrite ci-dessus:

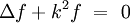$\Delta f + k^2 f \ = \ 0$ (équation de Helmholtz)

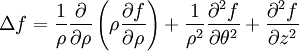$\Delta f = {1 \over \rho} {\partial \over \partial \rho} \left( \rho {\partial f \over \partial \rho} \right) + {1 \over \rho^2} {\partial^2 f \over \partial \theta^2} + {\partial^2 f \over \partial z^2 }$ (Laplacien en coordonnées cylindriques)

${1 \over \rho} {\partial \over \partial \rho} \left( \rho {\partial f \over \partial \rho} \right) + k^2 f = 0$

${\partial^2 f \over \partial \rho^2} + {1 \over \rho} {\partial f \over \partial \rho} + k^2 f = 0$

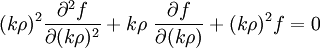$(k\rho)^2 {\partial^2 f \over \partial (k \rho)^2} + k\rho \ {\partial f \over \partial (k\rho)} + (k\rho)^2 f = 0$ (équation de Bessel avec x = k ρ et α = 0)

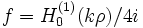Les conditions aux limites du problème imposent alors comme solution les fonctions de Hankel $f = H_{0}^{(1)}(k\rho)/4i$ .

Propriétés

Expression en fonction des Bessels de première espèce :

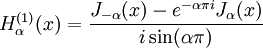
$H_{\alpha}^{(1)} (x) = \frac{J_{-\alpha} (x) - e^{-\alpha \pi i} J_{\alpha} (x)}{i \sin (\alpha \pi)}$

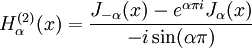
$H_{\alpha}^{(2)} (x) = \frac{J_{-\alpha} (x) - e^{\alpha \pi i} J_{\alpha} (x)}{- i \sin (\alpha \pi)}$

Relation sur α :

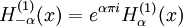
$H_{-\alpha}^{(1)} (x) = e^{\alpha \pi i} H_{\alpha}^{(1)} (x)$

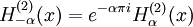
$H_{-\alpha}^{(2)} (x) = e^{-\alpha \pi i} H_{\alpha}^{(2)} (x)$

Comportement asymptotique :

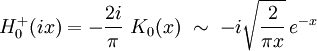
$H_{0}^{+}(ix) = - \frac{2i}{\pi} \ K_{0}(x) \ \sim \ - i \sqrt{\frac{2}{\pi x}} \, e^{-x}$

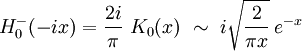
$H_{0}^{-}(-ix) = \frac{2i}{\pi} \ K_{0}(x) \ \sim \ i \sqrt{\frac{2}{\pi x}} \, e^{-x}$

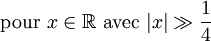
$\textrm{pour} \ x \in \mathbb{R} \ \textrm{avec} \ | x | \gg \frac{1}{4}$

Note

Une fonction de Hankel "oscille" si son argument x est uniquement réel, et converge de manière exponentielle si ce même argument est imaginaire pur.

Portail des mathématiques
Portail de la physique

Ce document provient de « Fonction de Hankel ».

Catégories : Fonction remarquable | Fonction hypergéométrique | Fonctions spéciales

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction de hankel de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Fonction De Hankel — Les fonctions de Hankel, du nom du mathématicien Hermann Hankel, notées et , sont des fonctions spéciales de la physique mathématique. Ce sont les solutions linéairement indépendantes de l équation de Bessel: où α est un nombre arbitraire réel ou … Wikipédia en Français
Fonction de Hankel — Les fonctions de Hankel, du nom du mathématicien Hermann Hankel, notées et , sont des fonctions spéciales de la physique mathématique. Ce sont les solutions linéairement indépendantes de l équation de Bessel: où α est un nombre arbitraire réel ou … Wikipédia en Français
fonction de Hankel — Hankelio funkcija statusas T sritis fizika atitikmenys: angl. Hankel function vok. Hankel Funktion, f rus. функция Ганкеля, f pranc. fonction de Hankel, f … Fizikos terminų žodynas
Fonction De Bessel — Les fonctions de Bessel, découvertes par le mathématicien suisse Daniel Bernoulli, portent le nom de Friedrich Bessel, et sont des solutions y de l équation différentielle de Bessel : pour tout nombre réel ou complexe n. Le cas le plus… … Wikipédia en Français
Fonction de bessel — Les fonctions de Bessel, découvertes par le mathématicien suisse Daniel Bernoulli, portent le nom de Friedrich Bessel, et sont des solutions y de l équation différentielle de Bessel : pour tout nombre réel ou complexe n. Le cas le plus… … Wikipédia en Français
Fonction de Bessel sphérique — Les fonctions de Bessel sphériques sont des fonctions construites à partir des fonctions de Bessel classiques et qui interviennent dans certains problèmes possédant une symétrie sphérique. Elles sont définies par : En particulier, j0… … Wikipédia en Français
Hankel function — Hankelio funkcija statusas T sritis fizika atitikmenys: angl. Hankel function vok. Hankel Funktion, f rus. функция Ганкеля, f pranc. fonction de Hankel, f … Fizikos terminų žodynas
Hankel-Funktion — Hankelio funkcija statusas T sritis fizika atitikmenys: angl. Hankel function vok. Hankel Funktion, f rus. функция Ганкеля, f pranc. fonction de Hankel, f … Fizikos terminų žodynas
Fonction spéciale — Interférences d ondes émises par deux sources cylindriques. Le phénomène s interprète à l aide des fonctions de Bessel. L analyse mathématique regroupe sous le terme de fonctions spéciales un ensemble de fonctions analytiques non élémentaires[1] … Wikipédia en Français
Fonction de Bessel — En mathématiques, et plus précisément en analyse, les fonctions de Bessel, découvertes par le mathématicien suisse Daniel Bernoulli, portent le nom du mathématicien allemand Friedrich Bessel. Bessel développa l analyse de ces fonctions en 1817… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonction de hankel