- Fonction caracteristique d'une variable aleatoire
-
Fonction caractéristique d'une variable aléatoire
La fonction caractéristique d'une variable aléatoire réelle X est la fonction à valeurs complexes définie sur
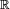 par
parSi cette variable aléatoire a une densité alors la fonction caractéristique est la transformée de Fourier inverse (à un facteur
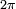 près suivant la convention) de la densité. Il arrive que l'on prenne
près suivant la convention) de la densité. Il arrive que l'on prenne ![\scriptstyle\ \phi_X(t) = E[e^{2i\pi tX}].](/pictures/frwiki/51/3ad54e1f3cb02e48c9245afe58a0b313.png)
Plus généralement, la fonction caractéristique d'une variable aléatoire X à valeurs dans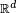 est la fonction à valeurs complexes définie sur
est la fonction à valeurs complexes définie sur 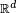 par
paroù
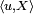 est le produit scalaire de u avec X.
est le produit scalaire de u avec X.
Lorsque la variable aléatoire X est discrète, on définit sa fonction génératrice paravec z complexe (quand cela a un sens). Avec les notations précédentes on a donc
cette fonction G est donc en fait un prolongement de
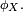
Propriétés de la fonction caractéristique
- Elle détermine de façon unique la loi d'une variable aléatoire au sens où
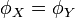 (égalité de fonctions) équivaut à "
(égalité de fonctions) équivaut à "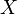 et
et 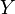 ont la même loi."
ont la même loi."
- Si X et Y sont deux variables aléatoires indépendantes,
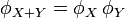 . Plus généralement, si
. Plus généralement, si 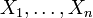 sont des variables aléatoires indépendantes dans leur ensemble, alors
sont des variables aléatoires indépendantes dans leur ensemble, alors 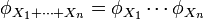 .
.
- En appliquant alors la transformée de Fourier à φX + Y cela permet de retrouver la loi de X+Y.
- Il y a aussi une relation entre les moments et la fonction caractéristique d'une variable aléatoire. Lorsque les moments existent et que la série converge :
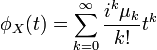 où μk est le moment d'ordre k.
où μk est le moment d'ordre k.
- Cette relation sert parfois pour calculer la moyenne (premier moment) et la variance d'une variable aléatoire. Plus explicitement
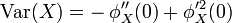 .
.
- La relation suivante sert, par exemple, à calculer la fonction caractéristique d'une variable centrée réduite, à partir de la fonction caractéristique de la variable de départ :
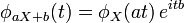 .
.
Voir aussi
- Portail des probabilités et des statistiques
Catégorie : Probabilités
Wikimedia Foundation. 2010.

![\begin{align}
\varphi_{X}(t)&=\mathbb{E}\left[e^{itX}\right]
\\
&=\mathbb{E}\left[\cos (tX)\right]+i\ \mathbb{E}\left[\sin (tX)\right].
\end{align}](/pictures/frwiki/52/4c7a574e5f40380e47b74f19afcc2b5f.png)
![\phi_X(u) = \mathbb{E}\left[e^{i \langle u , X \rangle}\right]\,](/pictures/frwiki/54/6fabbecb1941ff25deb4f6d0f57a6ec6.png)
![G(z)=\mathbb{E}\left[z^X\right]](/pictures/frwiki/53/5da28c65b8b923d8c703d18a89c0b0f7.png)
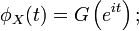
![1=\phi_X(0),\qquad\mathbb{E}[X]=-i\,\phi^{\prime}_X(0),\qquad\mathbb{E}\left[X^2\right]=-\,\phi^{\prime\prime}_X(0)](/pictures/frwiki/102/f428abf04d6887193aaac72520c24f3b.png)