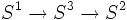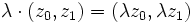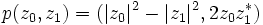Fibration de hopf

Fibration de Hopf

En géométrie la fibration de Hopf donne une partition de la sphère à 3-dimensions S³ par des grands cercles. Plus précisément, elle définit une structure fibrée sur S³. L'espace de base est la sphère à 2-dimensions S², la fibre modèle est un cercle S¹. Ceci signifie notamment qu'il existe une application p de projection de S³ sur S², telle que les images réciproques de chaque point de S² soient des cercles.

Cette structure a été découverte par Heinz Hopf en 1931. Cette fibration peut aussi être interprétée comme un fibré principal, de groupe structural le groupe S¹ des complexes de module 1.

$S^1 \to S^3 \to S^2\,$

Construction dans un plan complexe

La sphère S³ peut être identifiée à l'ensemble des éléments (z₀, z₁) de C² qui vérifient |z₀|² + |z₁|² = 1. On fait agir sur ce sous-espace le groupe des complexes de module 1, par la formule

$\lambda\cdot(z_0,z_1)=(\lambda z_0,\lambda z_1)$

Les orbites sous cette action de groupe sont clairement des cercles. L'espace quotient est l'espace projectif complexe CP¹, qui s'identifie à S².

Représentation de la fibration de Hopf à l'aide d'anneaux entrelacés.

Pour construire une application de projection adaptée à ces notations, on peut introduire l'application de Hopf

$p(z_0,z_1) = (|z_0|^2-|z_1|^2, 2z_0z_1^*)$

le premier élément du couple étant réel, le second complexe, on peut voir le résultat comme un point de R³. Si en outre |z₀|² + |z₁|² = 1, alors p (z₀, z₁) appartient à la sphère unité. Enfin, on observe que p (z₀, z₁) = p (z₂, z₃) si et seulement s'il existe λ de module 1 tel que (z₂, z₃) = (λz₀, λz₁).

La représentation ci-contre donne une idée de la disposition des fibres-cercles. Il s'agit d'une vue de la sphère S³ par projection stéréographique. Cette vue remplit tout l'espace et le point diamétralement opposé au centre de la figure est le point à l'infini. Il convient donc d'ajouter aux cercles représentés d'autres cercles continuant à remplir l'espace et un axe perpendiculaire au plan de la photo, qui est le cercle passant par le point à l'infini.

Extension

Par le même procédé toute sphère de dimension impaire S²ⁿ⁺¹ apparaît comme un espace fibré sur l'espace projectif CPⁿ, avec pour fibres des cercles. Il s'agit en fait d'une restriction du fibré tautologique sur CPⁿ : chaque fibre de ce dernier est une droite complexe, qu'on restreint en un cercle.

Portail des mathématiques

Ce document provient de « Fibration de Hopf ».

Catégories : Topologie différentielle | Cercle et sphère

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fibration de hopf de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Fibration De Hopf — En géométrie la fibration de Hopf donne une partition de la sphère à 3 dimensions S3 par des grands cercles. Plus précisément, elle définit une structure fibrée sur S3. L espace de base est la sphère à 2 dimensions S2, la fibre modèle est un… … Wikipédia en Français
Fibration de Hopf — En géométrie la fibration de Hopf donne une partition de la sphère à 3 dimensions S3 par des grands cercles. Plus précisément, elle définit une structure fibrée sur S3. L espace de base est la sphère à 2 dimensions S2, la fibre modèle est un… … Wikipédia en Français
Hopf — Heinz Hopf Heinz Hopf (à la droite) à Oberwolfach, à côté de Hellmuth Kneser Heinz Hopf (19 novembre, 1894 – 3 juin, 1971) était un mathématicien né à Gräbschen, en Allemagne. Il a montré très jeune des aptitudes mathématiques. Il est entré en… … Wikipédia en Français
Hopf fibration — In the mathematical field of topology, the Hopf fibration (also known as the Hopf bundle or Hopf map) describes a 3 sphere (a hypersphere in four dimensional space) in terms of circles and an ordinary sphere. Discovered by Heinz Hopf in 1931, it… … Wikipedia
Fibration — In mathematics, especially algebraic topology, a fibration is a continuous mapping:p:E o B,satisfying the homotopy lifting property with respect to any space. Fiber bundles (over paracompact bases) constitute important examples. In homotopy… … Wikipedia
Heinz Hopf — Ne doit pas être confondu avec Eberhard Hopf. Heinz Hopf (à la droite) à l institut de mathématiques d Oberwolfach, à côté de Hellmuth Kneser … Wikipédia en Français
Enlacement De Hopf — Entrelacs de Hopf Un enlacement de Hopf (en rouge et vert) et une de ses surfaces de Seifert. En mathématiques, l entrelacs de Hopf est un des modèles les plus simples étudiés en théorie des nœuds. C est l entrelacs non trivial et non connexe le… … Wikipédia en Français
Enlacement de Hopf — Entrelacs de Hopf Un enlacement de Hopf (en rouge et vert) et une de ses surfaces de Seifert. En mathématiques, l entrelacs de Hopf est un des modèles les plus simples étudiés en théorie des nœuds. C est l entrelacs non trivial et non connexe le… … Wikipédia en Français
Enlacement de hopf — Entrelacs de Hopf Un enlacement de Hopf (en rouge et vert) et une de ses surfaces de Seifert. En mathématiques, l entrelacs de Hopf est un des modèles les plus simples étudiés en théorie des nœuds. C est l entrelacs non trivial et non connexe le… … Wikipédia en Français
Entrelacs de Hopf — Un enlacement de Hopf (en rouge et vert) et une de ses surfaces de Seifert. En mathématiques, l entrelacs de Hopf est un des modèles les plus simples étudiés en théorie des nœuds. C est l entrelacs non trivial et non connexe le plus simple. Il… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fibration de hopf