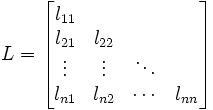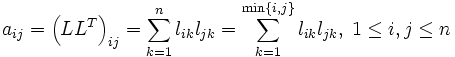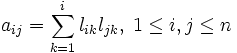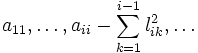Factorisation de cholesky

Factorisation de Cholesky

La factorisation de Cholesky, nommée d'après André-Louis Cholesky, consiste, pour une matrice symétrique semi définie positive A, à déterminer une matrice triangulaire inférieure L tel que : A=LL^T.

La matrice L est en quelque sorte une « racine carrée » de A. Cette décomposition permet notamment de calculer la matrice inverse A^-1, de calculer le déterminant de A (égal au carré du produit des éléments diagonaux de L) ou encore de simuler une loi multinormale. Elle est aussi, utilisée en chimie quantique pour accélérer les calculs (voir Décomposition de Cholesky (chimie quantique)).

Exemple

La matrice symétrique A :

$\begin{pmatrix} 1 & 1 & 1 & 1 \\ 1 & 5 & 5 & 5 \\ 1 & 5 & 14 & 14 \\ 1 & 5 & 14 & 15 \\ \end{pmatrix}$

est égale au produit à droite de la matrice triangulaire L :

$\begin{pmatrix} 1 & 0 & 0 & 0 \\ 1 & 2 & 0 & 0 \\ 1 & 2 & 3 & 0 \\ 1 & 2 & 3 & 1 \\ \end{pmatrix}$

et de sa transposée L^T.

Théorème

Factorisation de Cholesky d'une matrice :

Si A est une matrice symétrique définie positive, il existe au moins une matrice réelle triangulaire inférieure L telle que :

A=LL^T

On peut également imposer que les éléments diagonaux de la matrice L soient tous positifs, et la factorisation correspondante est alors unique.

Algorithme

On cherche la matrice :

$L=\begin{bmatrix} l_{11}\\ l_{21} & l_{22}\\ \vdots & \vdots & \ddots\\ l_{n1} & l_{n2} & \cdots & l_{nn} \end{bmatrix}$

De l'égalité A=LL^T on déduit :

$a_{ij}=\left(LL^{T}\right)_{ij}={\sum_{k=1}^{n}l_{ik}l_{jk}}={\sum_{k=1}^{\min\left\{ i,j\right\} }l_{ik}l_{jk}},\;1\leq i,j\leq n$

puisque l_pq=0 si 1≤p<q≤n.

La matrice A étant symétrique, il suffit que les relations ci-dessus soient vérifiées pour i≤j, c'est-à-dire que les éléments l_ij de la matrice L doivent satisfaire :

$a_{ij}={\sum_{k=1}^{i}l_{ik}l_{jk}},\;1\leq i,j\leq n$

Pour i=1, on détermine la première colonne de L :

a 11 = l 11 l 11

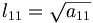
d'où $l_{11}=\sqrt{a_{11}}$

a 1 j = l 11 l j 1

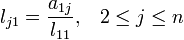
d'où $l_{j1}=\frac{a_{1j}}{l_{11}},\;\;\;2\leq j\leq n$

On détermine la i^ème colonne de L 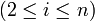$(2\leq i\leq n)$ , après avoir calculé les (i-1) premières colonnes :

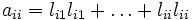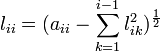
$a_{ii}=l_{i1}l_{i1}+\ldots+l_{ii}l_{ii}$ d'où $l_{ii}=({a_{ii}-{\sum_{k=1}^{i-1}l_{ik}^{2}}})^{\frac{1}{2}}$

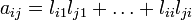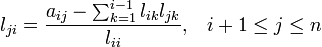
$a_{ij}=l_{i1}l_{j1}+\ldots+l_{ii}l_{ji}$ d'où $l_{ji}=\frac{a_{ij}-{\sum_{k=1}^{i-1}l_{ik}l_{jk}}}{l_{ii}},\;\;\;i+1\leq j\leq n$

Il résulte du théorème précédent qu'il est possible de choisir tous les éléments l_ii>0 en assurant que toutes les quantités

$a_{11},\ldots,a_{ii}-{\sum_{k=1}^{i-1}l_{ik}^{2}},\ldots$

sont positives.

Voir aussi

Portail des mathématiques

Ce document provient de « Factorisation de Cholesky ».

Catégorie : Analyse numérique matricielle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Factorisation de cholesky de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Factorisation De Cholesky — La factorisation de Cholesky, nommée d après André Louis Cholesky, consiste, pour une matrice symétrique semi définie positive A, à déterminer une matrice triangulaire inférieure L tel que : A=LLT. La matrice L est en quelque sorte une… … Wikipédia en Français
Factorisation de Cholesky — La factorisation de Cholesky, nommée d après André Louis Cholesky, consiste, pour une matrice symétrique définie positive A, à déterminer une matrice triangulaire inférieure L telle que : A=LLT. La matrice L est en quelque sorte une… … Wikipédia en Français
Décomposition de Cholesky — Factorisation de Cholesky La factorisation de Cholesky, nommée d après André Louis Cholesky, consiste, pour une matrice symétrique semi définie positive A, à déterminer une matrice triangulaire inférieure L tel que : A=LLT. La matrice L est… … Wikipédia en Français
Methode de Cholesky — Factorisation de Cholesky La factorisation de Cholesky, nommée d après André Louis Cholesky, consiste, pour une matrice symétrique semi définie positive A, à déterminer une matrice triangulaire inférieure L tel que : A=LLT. La matrice L est… … Wikipédia en Français
Factorisation LU — Décomposition LU En algèbre linéaire, la décomposition LU est une méthode de décomposition d une matrice en une matrice triangulaire inférieure L (comme Low , bas) et une matrice triangulaire supérieure U (comme Up , haut). Cette décomposition… … Wikipédia en Français
André-Louis Cholesky — (15 octobre 1875 à Montguyon 31 août 1918 à Bagneux) est un polytechnicien et officier français, ingénieur topographe et géodésien. Il est célèbre pour sa méthode de résolution des systèmes d équations linéaires, toujours… … Wikipédia en Français
Andre-Louis Cholesky — André Louis Cholesky André Louis Cholesky (15 octobre 1875 à Montguyon 31 août 1918) était un mathématicien et officier français. Il entre en 1895 à l École polytechnique. De 1897 à 1899, il est élève de l École d Application… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Décomposition LU — En algèbre linéaire, la décomposition LU est une méthode de décomposition d une matrice comme produit d une matrice triangulaire inférieure L (comme Low , bas) et une matrice triangulaire supérieure U (comme Up , haut). Cette décomposition est… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Factorisation de cholesky