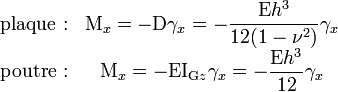- Essai de flexion
-
Flexion (matériau)
La flexion est la déformation d'un objet qui se traduit par une courbure. Dans le cas d'une poutre, elle tend à rapprocher les deux extrémités de la poutre. Dans le cas d'une plaque, elle tend à rapprocher deux points diamétralement opposés sous l'action.
L'essai de flexion d'une poutre est un essai mécanique utilisé pour tester la résistance en flexion. On utilise la flexion dite « trois points » et la flexion dite « quatre points ».
Sommaire
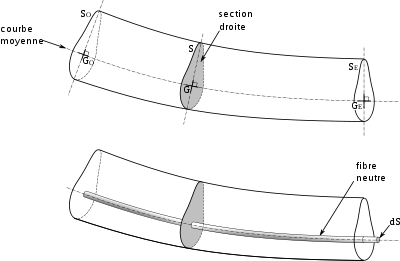
Cas d'une poutre
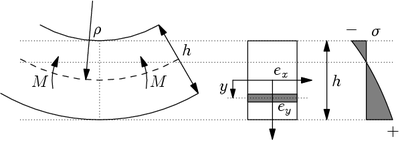
En théorie des poutres, on considère des fibres, c'est-à-dire des petits cylindres de matières générés par une portion dS et une courbe parallèle à la courbe moyenne (la « direction de la poutre ») ; la courbe moyenne passe par les centres de gravité des sections droites (sections perpendiculaires à la courbe moyenne). Les fibres situées vers l'extérieur de la flexion sont en extension, elles sont soumises à de la traction. Les fibres situées à l'intérieur de la flexion sont en compression.
La fibre générée par la courbe moyenne est appelée « fibre neutre ». Elle garde sa longueur lors de la flexion.
Par la suite, sauf mention contraire, nous supposerons que la poutre est rectiligne avant la flexion (la courbe moyenne forme une droite) et que les sections sont symétriques. Nous considèrerons au début la flexion plane, c'est-à-dire avec des charges agissant dans un plan de symétrie de la poutre.
Déformation
Du fait de l'hypothèse de Bernoulli (lors de la déformation, les sections droites restent perpendiculaires à la courbe moyenne),
- la fibre neutre a un allongement nul ;
- les fibres à l'extérieur de la courbure sont étirées ;
- les fibres à l'intérieur de la courbure sont comprimées.
la déformation longitudinale ε varie de manière linéaire en fonction de y.
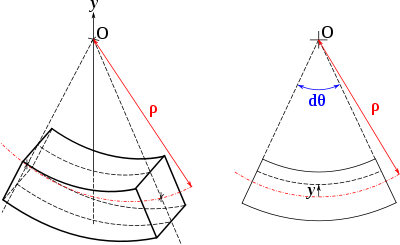
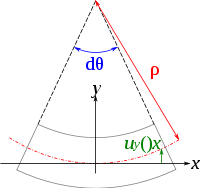
Par ailleurs, en considérant une poutre droite, si l'on appelle uy(x) la flèche, c'est-à-dire le déplacement vertical du point de la courbe moyenne situé à l'abscisse x en raison de la flexion, on a, d'après la définition générale du rayon de courbure :
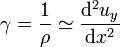 .
.
Le graphique uy(x) donne la forme de la courbe moyenne, encore appelée « déformée de la poutre ».
DémonstrationSi l'on considère un élément infinitésimal de la poutre, alors les fibres forment des arcs de cercle concentriques de même angle dθ. Si ρ est le rayon de courbure de la fibre neutre (y = 0), alors la longueur l d'un arc situé à une ordonnée y vaut :
si l 0 est la longueur initiale des fibres. On voit que la déformation longitudinale
varie de manière linéaire en fonction de y.
Efforts de cohésion
Si l'on considère les efforts de cohésion (voir les articles Théorie des poutres et Torseur de cohésion), la flexion résulte des moments fléchissants Mfy et Mfz.
Nous considérerons ici la convention des efforts à droite.
On remarque que la valeur de l'effort tranchant est la dérivée du moment fléchissant par rapport à la position x du point considéré :
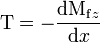 .
.
Contraintes
Contrainte normale
Plaçons-nous dans le cas d'un moment fléchissant Mfz positif ; dans le plan (Gxy), les fibres sont concentriques, le centre O est situé vers le haut. La longueur de l'arc est proportionnelle au rayon, c'est-à-dire qu'elle varie linéairement en fonction de l'abscisse y considérée. De même, la contrainte normale à la section varie linéairement en fonction de y et l'on trouve :
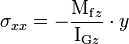 .
.
où IGz est le moment quadratique d'axe (Gz), calculé en fonction de la forme de la section droite.
Le risque de rupture se situe sur la face en extension de la poutre. Si l'on appelle -V l'ordonnée du point situé sur cette face, la contrainte y vaut :
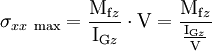 .
.
La grandeur IGz/V est appelée « module de flexion ».
Si la poutre est symétrique et de hauteur h, on a
DémonstrationDe même que la longueur des fibres, l'allongement relatif ε est proportionnel à y :
donc, d'après la loi de Hooke, la contrainte varie également de manière linéaire :
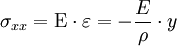 ,
,
la quantité E/ρ étant à déterminer. Un petit élément de surface dS reçoit une force dF valant
et le moment dM de cette force par rapport au point G (0,0,0) appartenant donc à la ligne moyenne :
Le moment fléchissant résulte de l'ensemble de ces moments, et en intégrant sur la section droite, on trouve :
avec
On a alors :
soit
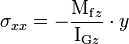 .
.
- Note
- Comme c'est la valeur absolue de la contrainte qui nous intéresse, et que de toute manière le signe dépend de la convention choisie, on trouve souvent l'expression
Cisaillement
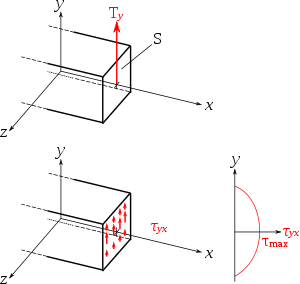
Dans la plupart des cas, le moment fléchissant s'accompagne d'un effort tranchant (Ty avec Mfz, Tz avec Mfy). Ce la génère de la cission (τxy pour Ty et τxz pour Tz). Cette contrainte de cisaillement ne génère que peu de risque de rupture et est donc généralement négligée (modèle de Bernoulli).
La répartition des contraintes n'est pas uniforme : la contrainte sur une surface libre est nécessairement dans le plan de la surface, donc la cission sur les faces extérieure est nulle. On a donc une cission qui croît lorsque l'on s'approche de la fibre neutre. La contrainte maximale vaut alors, si S est l'aire de la section droite :
- poutre de section rectangulaire pleine :
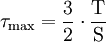 ;
; - poutre de section circulaire pleine :
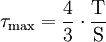 ;
; - tube circulaire mince :
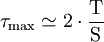 ;
;
où S est l'aire de la section droite. On voit que sur ces exemples là, la contrainte est 1,5 à 2 fois supérieure au cas du cisaillement simple.
DémonstrationOn se place dans le cas de la flexion trois points entre les deux premiers appuis. On considère un élément de poutre comprise entre deux sections droites placées en x et x + dx, et entre le feuillet d'ordonnée y0 et le bas de la poutre d'ordonnée V. Au niveau du feuillet, la largeur de la poutre est l.
Cet élément de matière est soumis :
- à des forces normales aux sections droites ;
- à la force résultant du cisaillement ; elle s'exerce sur une face rectangulaire de dimensions l×dx.
Le moment fléchissant varie, donc la force normale sur chacune des sections droites est différente. On peut donc en déduire la cission par le principe fondamental de la statique (PFS).
L'effort tranchant Ty est uniforme entre 0 et le milieu de la poutre, et l'on a :
- Mfz = Ty×x.
La force sur la face de gauche vaut donc
où
est le moment statique de la portion de la section droite comprise entre V et y0.
La force sur la face de droite vaut :
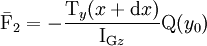 .
.
La force résultante vaut
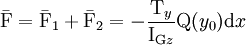 .
.
Le PFS s'écrit donc :
soit
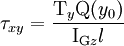 .
.
On a pour les sections évoquées :
- poutre de section rectangulaire pleine de hauteur h et de largeur l :
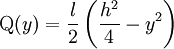 ;
; - poutre de section circulaire pleine de rayon r :
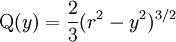 ;
; - tube circulaire mince délimité par deux cylindres de rayons r et R :
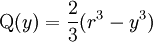 .
.
Calcul de la déformée
Nous avons vu ci-dessus que
- L'on néglige la déformation par cisaillement ;
- L'on peut déterminer la courbure γ et le rayon de courbure ρ en fonction du moment fléchissant Mfz, du facteur de forme IGz et du module de Young E :
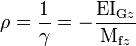 ;
;
- L'on dispose d'une équation différentielle reliant la déformée uy à ρ et à γ :
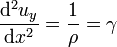 .
.
On peut donc déterminer la déformée par intégration double :
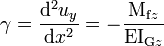 .
.
Si la poutre est de section uniforme (IGz ne varie pas) de même matériau (E ne varie pas), on se contente d'intégrer le moment fléchissant :
où A et B sont des constantes d'intégration déterminées à partir des conditions limites :
- aux points de liaison, on a uy = 0 ;
- aux points d'encastrement, on a u’y = 0 ;
- si le problème est symétrique par rapport à la section droite médiane, on a u’y = 0 au centre de la poutre.
On s'intéresse en général à la valeur maximale de uy, la « flèche » de la poutre, qui détermine l'état limite en service (ELS, valeur de chargement à ne pas dépasser pour que la forme de la poutre reste compatible avec sa fonction).
- Note
- On trouve souvent la notation abusive
- EIGzy ’’ = Mfz.
- y désignant alors le déplacement.
- Par ailleurs, les expressions exactes sont :
- et donc
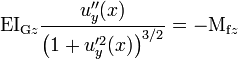 .
.
Flexion en grande déformation
Lorsque le rayon de courbure ρ est inférieur à dix fois la hauteur h de la section
- ρ < h/10,
les hypothèses ne sont plus valables. Si toutefois on considère que :
- les sections droites restent planes ;
- les contraintes normales à la section sont indépendantes des contraintes parallèles à la section ;
alors la contrainte normale résultant du moment fléchissant devient
où S est l'aire de la section.
Flexion déviée
La flexion déviée est le cas où les charges ne sont pas dans un plan de symétrie de la poutre ; c'est notamment toujours le cas lorsque la poutre ne présente pas de plan de symétrie (par exemple une cornière).
Poutre symétrique
Dans le cas d'une poutre symétrique, on peut décomposer le vecteur moment de flexion en deux composantes Mfy et Mfz non nulles. Si l'on reste en petites déformations, le système est linéaire, on peut donc considérer que l'on a une superposition de deux flexions planes. La contrainte normale vaut donc
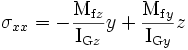 .
.
Le plan sur lequel la contrainte s'annule est appelé « plan neutre ».
Poutre non symétrique
On détermine les axes principaux d'inertie Y et Z (voir l'article Matrice d'inertie), puis l'on se ramène au cas précédent en se plaçant dans le repère (GxYZ) :
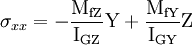 .
.
Cas isostatiques
Flexion trois points
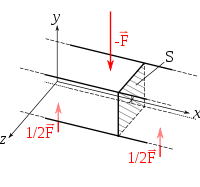
La flexion trois point est un essai mécanique classique. Il représente le cas d'une poutre posée sur deux appuis simples (appuis linéaires rectilignes qui, dans un problème plan, équivalent à une liaison ponctuelle) et soumise à une charge concentrée, appliquée au milieu de la poutre avec elle aussi un contact simple. On modélise souvent un des appuis comme un pivot afin d'avoir une poutre qui ne se déplace pas horizontalement.
Dans la figure ci-contre, la poutre a une longueur L et la charge centrale est P.
L'effort tranchant est constant en valeur absolue : il vaut la moitié de la charge centrale, P/2. Il change de signe au milieu de la poutre. Le moment fléchissant varie de manière linéaire entre une extrémité, où il vaut 0, et le centre où sa valeur absolue vaut PL/4 ; c'est là que le risque de rupture est le plus important.
Le profil de la poutre est décrit par un polynôme du troisième degré (fonction en x3) sur une moitié de poutre (l'autre moitié étant symétrique).
Poutre sur deux appuis avec une charge ponctuelle
Ce cas est la généralisation de la flexion trois points : la charge n'est pas nécessairement appliquée au centre. Cela permet, par exemple, de représenter une charge roulante.
L'analyse entre une extrémité et le point d'application de la charge est la même que pour la flexion trois points, mais le problème n'est plus symétrique.
Poutre encastrée
Une poutre encastrée (clamped beam, cantilever) représente le cas d'une hampe de drapeau, d'un poteau scellé dans le sol, d'une poutre en porte à faux (par exemple une potence).
On peut remarquer qu'elle se comporte comme la moitié d'une poutre en flexion trois points, l'encastrement correspondant au centre. Le moment fléchissant maximal est au niveau de l'encastrement, c'est là que le risque de rupture est le plus important.
Flexion quatre points
La différence principale avec la flexion trois points se situe entre les deux charges : le moment fléchissant est constant et l'effort tranchant est nul. Cette situation est qualifiée de flexion pure.
Poutre sur deux appuis avec une charge répartie uniforme
Une charge uniforme permet de décrire le poids propre de la poutre, ou encore le poids d'un liquide dans le cas d'une canalisation ou d'un réservoir.
Poutre sur deux appuis avec une charge répartie linéairement
Cas hyperstatiques de degré 3
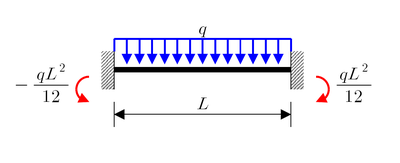
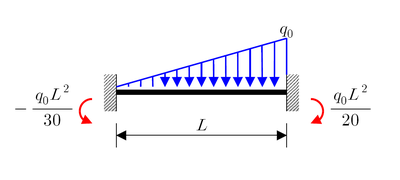
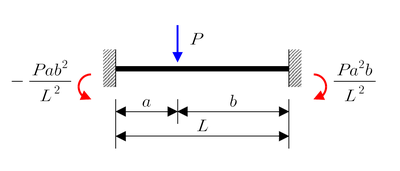
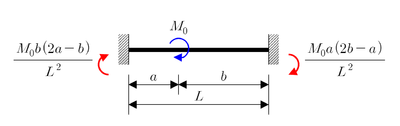
Poutre biencastrée
Charge continue uniformément répartie q
Charge continue de répartition linéaire avec un maximum de q0
Charge concentrée P
Couple M0Cas d'une plaque
Dans la théorie des plaques, on considère
- des feuillets, c'est-à-dire de fines tranches de matières parallèles aux faces de la plaque, le feuillet moyen étant situé au milieu de la plaque, et
- des fibre normales, c'est-à-dire de fins tubes de matière perpendiculaires au feuillet moyen.
Dans la théorie des plaques minces de Kirchhoff-Love, le feuillet moyen se courbe mais n'est pas étiré dans son plan (pas de déformation de « membrane »), et les fibres normales restent perpendiculaires au feuillet moyen au cours de la déformation. On peut donc exprimer simplement les déplacements u et v d'un point selon respectivement x et y en fonction de l'altitude z de ce point, de son déplacement w selon z et des angles θx et θy :
- u(x, y, z) ≃ z·θy(x, y) ;
- v(x, y, z) ≃ -z·θx(x, y) ;
![\begin{matrix}
\theta_x = \frac{\partial w}{\partial y} \text{ ;}\\ [1ex]
\theta_y = -\frac{\partial w}{\partial x} \text{.}\\
\end{matrix}](/pictures/frwiki/48/071f815cbb7574a9159daab8675917f4.png)
Dans l'absolu, l'hypothèse d'absence de déformation de membrane n'est valable que si la surface peut être développée, c'est-à-dire si elle n'a qu'une seule courbure (cylindre ou cône de révolution). Dans le cas général (voir les exemples de la sphère et de la selle de cheval), il y a nécessairement une étirement. L'hypothèse n'est donc valable que si le déplacement w est faible devant l'épaisseur h de la plaque.
Déformation
D'après la définition du tenseur des déformations, on a :
où γx est la courbure du feuillet moyen dans le plan xz et γy dans le plan yz.
Efforts de cohésion
Les moments fléchissants mxy, agissant sur la face normale à x et dont le vecteur est dirigé selon y, et myx, agissant sur la face normale à y et dont le vecteur est dirigé selon x, créent une répartition linéaire de la contrainte normale. Cette situation est similaire à celle de la poutre.
Contraintes
On peut évaluer les contraintes à partir de la loi de Hooke :
soit
où E est le module de Young et ν est le coefficient de Poisson.
On peut relier les contraintes normales aux moments fléchissants par le principe d'équivalence ; il faut pour cela choisir une convention, à l'instar des conventions des efforts à gauche ou à droite pour les poutres. Ici, nous choisissons de noter les moments positifs s'ils provoquent une courbure vers le bas, c'est-à-dire si la face supérieure est en compression (σii < 0 pour z > 0) et la face inférieure est en compression (σii > 0 pour z < 0).
Donc, si l'élément de matière fait dx × dy × h, alors
soit
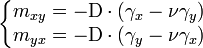 .
.
Le terme
est appelé rigidité flexionnelle. Il joue le même rôle que le facteur E⋅IGz pour la flexion d'une poutre.
Comme on a
on en déduit les équations différentielles :
![\left \{ \begin{matrix}
m_{xy} = - \mathrm{D} \cdot \left ( \frac{\partial^2 w}{\partial x^2} - \nu \frac{\partial^2 w}{\partial y^2} \right ) \\ [1ex]
m_{yx} = - \mathrm{D} \cdot \left ( \frac{\partial^2 w}{\partial y^2} - \nu \frac{\partial^2 w}{\partial x^2} \right ) \\
\end{matrix} \right .](/pictures/frwiki/97/a54d0e84c4255e10ab86ebda630b5760.png) .
.
Dans le cas général, mxy myx sont des fonctions de x et de y.
Cas particuliers
Distribution uniforme de moments sur les côtés d'une plaque rectangulaire
Nous allons d'abord nous placer dans le cas simple d'une plaque rectangulaire soumise à des moments uniformes à ses bords ; ce cas ne correspond pas à un cas réel particulièrement intéressant, mais permet d'avoir simplement un certain nombre de résultats de manière simple. Cette situation est similaire à la flexion pure d'une poutre (partie centrale de la flexion à quatre points).
Dans notre cas particulier, On est dans le cas de torseurs couples. Si l'on considère un élément de matière n'importe où dans la plaque, on a donc :
- mxy = Mx ;
- myx = My.
Ce sont des constantes, on a donc
Dans ce cas-là, la solution est simple : on obtient des courbures uniformes :
avec
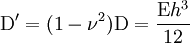 .
.
Si l'un des couples extérieurs est nul, par exemple My = 0, alors on a
- γy = -νγx,
c'est-à-dire que les deux courbures principales sont opposées (courbe « anticlastique » de type selle de cheval). Dans le cas particulier où My = νMx, on a
- γy = 0
c'est-à-dire que l'on n'a qu'une courbure que dans un sens. Ce cas est similaire à la flexion pure d'une poutre, mais le résultat est légèrement différent :
Le facteur de différence 1/(1-ν²) provient du fait que la plaque n'a pas la possibilité de s'étendre librement sur les côtés. Dans le cas des métaux (ν ≃ 0,3), on a un écart d'environ 10 % (1/(1-ν²) ≃ 1,10).
Si l'on a My = Mx, alors
- γy = γx,
la plaque prend donc la forme d'une calotte de sphère. Ceci est en fait vrai quelle que soit la forme de la plaque, pour toute répartition uniforme des moments.
Pression uniforme
- Plaque carrée appuyée
Dans le cas d'une plaque carrée de côté a simplement appuyée chargée par une pression uniforme p0, la flèche maximale wmax est au centre et vaut :
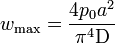 .
.
- Plaque circulaire encastrée
Dans le cas d'une plaque circulaire de rayon R encastrée, la flèche à une distance r du centre vaut
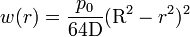 ;
;
la flèche maximale est au centre et vaut
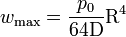 .
.
Notons que l'on peut également écrire la flèche sous la forme
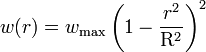 .
.
Application à la construction
Le poids porté sur une poutre ou un plancher comprimera l'élément et l'étirera. Le centre n'est soumis à aucune déformation et peut même être évidé pour des questions d'économie de matériaux dans un but financier ou pour réduire le poids propre de l'élément. C'est la raison pour laquelle on utilise des tubes, des cornières ou des profilés (fer U, fer I, profilés d'aluminium), des planchers à caisson, …
Voir aussi
Bibliographie
- Jean-Louis Fanchon, Guide de mécanique, Nathan, 2001.
p. 265-396
- Claude Hazard, Frédy Lelong, Bruno Quinzain, Mémotech — Structures métalliques, Casteilla, 1997.
p. 326-336
- D. Spenlé, R. Gourhant, Guide du calcul en mécanique, Hachette, 2003.
p. 130-208
Articles connexes
Catégories : Résistance des matériaux | Essai mécanique
Wikimedia Foundation. 2010.



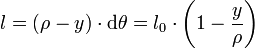
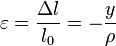


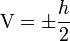
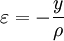
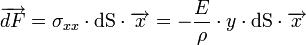
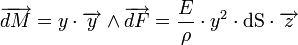
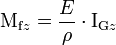
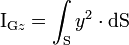
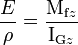
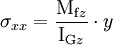

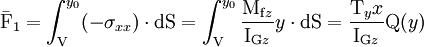
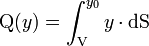
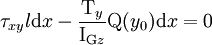
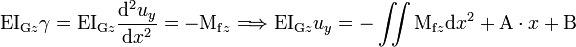
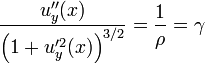
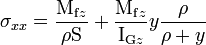





![\left \{
\begin{array}{l}
\varepsilon_{11} = z \cdot \frac{\partial \theta_y}{\partial x} = -z \cdot \gamma_x \\ [1ex]
\varepsilon_{22} = -z \cdot \frac{\partial \theta_x}{\partial y} = -z \cdot \gamma_y \\ [1ex]
\end{array}
\right .](/pictures/frwiki/55/7f58fba88000f08b894d578e6437b737.png)

![\left \{ \begin{matrix}
\varepsilon_{11} = \dfrac{1}{\mathrm{E}} \cdot( \sigma_{11} - \nu \cdot \sigma_{22} ) \\ [2ex]
\varepsilon_{22} = \dfrac{1}{\mathrm{E}} \cdot( \sigma_{22} - \nu \cdot \sigma_{11} ) \\
\end{matrix} \right .](/pictures/frwiki/57/9f5f2451cda52a1e89bda69518438c1c.png)
![\left \{ \begin{matrix}
\sigma_{11} = -\dfrac{\mathrm{E}}{1-\nu^2} \cdot( \gamma_x + \nu \gamma_y ) \cdot z \\ [2ex]
\sigma_{22} = -\dfrac{\mathrm{E}}{1-\nu^2} \cdot( \gamma_y + \nu \gamma_x ) \cdot z \\
\end{matrix} \right .](/pictures/frwiki/102/f8839cd26d48d4ed01a2669932abc907.png)
![\left \{ \begin{matrix}
m_{xy} \cdot \mathrm{d}y = \int_{-h/2}^{h/2} \left (\sigma_{11} \cdot z \cdot \mathrm{d}y \right ) \cdot \mathrm{d}z \\ [1ex]
m_{yx} \cdot \mathrm{d}x = \int_{-h/2}^{h/2} \left (\sigma_{22} \cdot z \cdot \mathrm{d}x \right ) \cdot \mathrm{d}z \\
\end{matrix} \right .](/pictures/frwiki/51/395c63019bcc093ee53612089617027f.png)
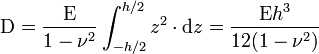
![\left \{ \begin{matrix}
\gamma_{x} \simeq \dfrac{\partial^2 w}{\partial x^2} \\ [2ex]
\gamma_{y} \simeq \dfrac{\partial^2 w}{\partial y^2} \\
\end{matrix} \right .](/pictures/frwiki/102/f1058604a056c6b400ee6574d9dc8370.png)

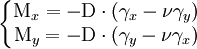
![\left \{ \begin{matrix}
\gamma_{x} = \dfrac{\mathrm{M}_x - \nu \mathrm{M}_y}{\mathrm{D}'} \\ [2ex]
\gamma_{y} = \dfrac{\mathrm{M}_y - \nu \mathrm{M}_x}{\mathrm{D}'} \\
\end{matrix} \right .](/pictures/frwiki/100/d50f19f93cd494b04232b1112f181aaa.png)